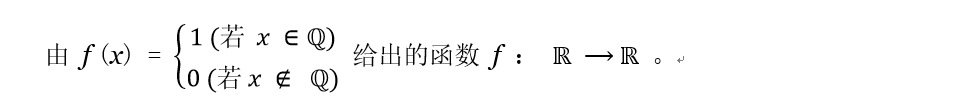数学分析专题
【数学分析笔记】第2章第4节收敛准则(1)
2. 数列极限 2.4 收敛准则 收敛数列一定有界,有界数列不一定收敛。 问题: (1)有界数列加什么条件可以保证收敛? (2)有界数列不加其他条件,可得到什么弱一些的结论? 2.4.1 单调有界定理 【定理2.4.1】单调有界数列必定收敛。(单调增加有上界或单调减少有下界) 【证】不妨设 { x n } \{x_{n}\} {xn}单调增加,有上界。 以 { x n } \{x_{n}
【数学分析笔记】第2章第2节数列极限(4)
2. 数列极限 2.2 数列极限 2.2.6 数列极限的四则运算 【定理2.2.5】设 lim n → ∞ x n = a , lim n → ∞ y n = b \lim\limits_{n\to\infty}x_{n}=a,\lim\limits_{n\to\infty}y_{n}=b n→∞limxn=a,n→∞limyn=b,则: (1) lim n → ∞ (
如何理解与学习数学分析——第二部分——数学分析中的基本概念——第10章——实数
第2 部分:数学分析中的基本概念 (Concepts in Analysis) 10. 实数(The Real Numbers) 本章介绍比率数(rational numbers)和非比数(irrational numbers)及其与十进制展开的关系。讨论了实数的公理,并解释了完备性公理对于区分实数和比率数为何必不可少,并证明关于序列和函数的直观而令人信服的结果。 10.1 数的
如何理解与学习数学分析——第二部分——数学分析中的基本概念——第9章——可积性
第2 部分:数学分析中的基本概念 (Concepts in Analysis) 9. 可积性(Integrability) 本章讨论了可积性(integrability)的概念(它不同于积分过程)。研究了反导数(antiderivative,或称原函数)和函数图像下面积之间的关系,然后通过对面积的近似建立了可积性的定义。给出了一个不可积函数的例子,并展示了如何在证明中使用Riemann条件(
如何理解与学习数学分析——第二部分——数学分析中的基本概念——第7章——连续性
第2 部分:数学分析中的基本概念 (Concepts in Analysis) 7. 连续性(Continuity) 本章首先讨论连续性的直观概念,并介绍与早期数学中常见的函数不同的函数。解释了连续性的定义,并演示了如何使用它来证明函数在一点上连续,以及证明有关连续函数的更一般定理。最后,将连续性与极限以及涉及不连续性的证明联系起来。 7.1 何谓连续(What is
数学分析复习:黎曼引理、黎曼-勒贝格引理
文章目录 黎曼引理、黎曼-勒贝格引理Riemann引理Riemann-Lebesgue引理 本篇文章适合个人复习翻阅,不建议新手入门使用 黎曼引理、黎曼-勒贝格引理 Riemann引理 我们知道一般情况下积分算子是无法保持乘法的,即 ∫ a b f ( x ) ⋅ g ( x ) d x ≠ ∫ a b f ( x ) d x ⋅ ∫ a b g ( x ) d x
漫步数学分析十四——连通集
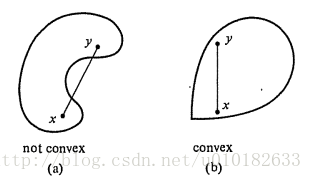
定义3 \textbf{定义3} 集合 A⊂Rn A\subset R^n为连通集,如果不存在两个非空开集 U,V U,V,使得 A⊂U∪V,A∩U≠∅,A∩V≠∅,A∩U∩V=∅ A\subset U\cup V,A\cap U\neq\emptyset,A\cap V\neq\emptyset,A\cap U\cap V=\emptyset。 直观上,集合 U,V U,V将 A A分成了两
漫步数学分析十一——紧集
在给出 Rn R^n中紧集的精确定义前,我们需要介绍一些术语。对于集合 A⊂Rn A\subset R^n,当且仅当存在一个常数 M≥0 M\geq0使得 A⊂D(0,M) A\subset D(0,M),那么就称该集合是有界的(bounded),所以一个集合被邻域原点的某个邻域 D(0,M) D(0,M)包住时,它就是有界的;换句话说,对于所有的 x∈A,∥x∥<M x\in A,\Vert x
漫步数学分析五——闭集
定义3 \textbf{定义3} 对于 Rn R^n中的集合 B B,如果它在RnR^n中的补(即集合 Rn∖B R^n\backslash B)是开集,那么它是闭集。 例如,单点是闭集,含有边界的单位圆组成的集合是闭集。大致来说,当集合包含它的边界点时它就是闭的(直观感觉可从图6中看出),如图1所示。 图1 存在既不是开集又不是闭集的集合。例如在 R1 R^1,中半
漫步数学分析三——开集
为了定义开集,我们首先介绍 ε−disc \varepsilon-\text{disc}的概念。 定义1 \textbf{定义1} 对于每个固定的 x∈Rn x\in R^n以及 ε>0 \varepsilon>0,集合 D(x,ε)={y∈Rn|d(x,y)<ε} D(x,\varepsilon)=\{y\in R^n|d(x,y)<\varepsilon\} 称为关
漫步数学分析三十九——隐函数定理
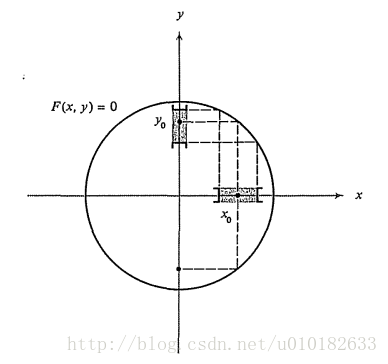
假设 x,y x,y被方程 F(x,y)=0 F(x,y)=0关联起来,我们会说这定义了一个函数 y=f(x) y=f(x)(或者说隐式定义了 y=f(x) y=f(x)),然后打算计算 dy/dx dy/dx。前面已经提到过,给定这样的 F F,一般不能显式求出yy,所以在没有求解之前知道这样的函数存在是非常重要的。 为了更好的理解给出的结论,考虑函数 F(x,y)=x2+y2−1 F(x,y
漫步数学分析三十六——泰勒定理
我们讨论一般函数 f:A⊂Rn→Rm f:A\subset R^n\to R^m的泰勒公式,为此我们首先讨论高阶导数。对于 f:Rn→R f:R^n\to R,定义高阶偏导没有问题;我们仅仅迭代偏导的过程 ∂2f∂x1∂x2=∂∂x1(∂∂x2f) \frac{\partial^2f}{\partial x_1\partial x_2}=\frac{\partial}{\parti
漫步数学分析三十五——均值定理
我们现在考虑两个非常重要的定理,也就是均值定理与泰勒(Taylor)定理。首先,我们考虑均值定理,我们先回顾一下基本微积分中的均值定理,如果 f:[a,b]→R f:[a,b]\to R是连续的,在 (a,b) (a,b)上可微,那么存在点 c∈(a,b) c\in(a,b)使得 f(b)−f(a)=f′(c)(b−a) f(b)-f(a)=f^\prime(c)(b-a),其中 f′=df/dx
漫步数学分析三十三——可微的条件
因为雅克比矩阵给出了有效的计算方法,因此我们知道通常的偏导存在就意味着导数 Df Df存在。不幸的是这结论在一般情况下是不成立的,例如将 f:R2→R f:R^2\to R 定义为 y=0,f(x,y)=x;x=0,f(x,y)=y; y=0,f(x,y)=x;x=0,f(x,y)=y;其余情况下 f(x,y)=1 f(x,y)=1,那么 ∂f/∂x,∂f/∂y \partial f/\parti
漫步数学分析二十八——狄利克雷与阿贝尔测试
在我们判断一致收敛的时候,某些情况下魏尔斯特拉斯M测试会失效,为此挪威数学家尼尔斯阿贝尔(Niels Abel)以及狄利克雷(Dirichlet)分别提出了两种测试方法,这些方法对许多实例都是非常有用的,尤其是研究傅里叶与幂级数的时候,当我们碰到一致收敛却不是绝对收敛的时候,这些方法非常重要。 定理13 \textbf{定理13}(阿贝尔测试) 令 A⊂Rm,φn:A→R A\subset R
漫步数学分析二十——一致连续
有时候,对连续的定义进行一些变形是非常有用的。这就是我们要介绍的一致连续函数(uniformly continuous function),精确的定义如下。 定义3 \textbf{定义3} 令 f:A→Rm,B⊂A f:A\to R^m,B\subset A,我们说 f f 在集合BB上一致连续,如果对每个 ε>0 \varepsilon>0,存在 δ>0 \delta>0使得 x,y∈B
漫步数学分析十九——介值定理
介值定理说明对于某区间上的连续函数,给定两个值后,可以取得两个值中间的所有值,如图1,图2中的不连续函数 f f不会取值1/21/2。简单来说,该定理告诉我们不连续函数可以从一个值调到另一个值,而连续函数必须通过所有中间值。 图1 介值定理不成立的另一方方式是定义域 A A是不连通的,如图3所示。因此关键的假设是ff是连续函数并且 f f定义在连通区域上。我们随后会看到定
漫步数学分析十八——紧集上连续函数的有界性
现在我们证明连续实值函数的一个重要性质,即有界定理。有界定理表明连续函数在紧集上是有界的并且在集合上的某些点取得最大值与最小值,准确的描述放到定理5中。 为了理解上面的结论,我们考虑非紧集上函数会发生什么情况。首先,连续函数不一定是有界的,图 ??? \ref{fig:4-5} 给出的是开区间 (0,1) (0,1) 上的函数 f(x)=1/x f(x)=1/x,随着 x x越来越靠近0,函数变
数学分析复习: 连续函数、可微函数的重要结论梳理
文章目录 连续函数、可微函数的重要结论梳理总结细节1.有界性定理2.最值定理3.介值定理4.中值定理5.洛必达法则6.泰勒公式 本篇文章适合个人复习翻阅,不建议新手入门使用 连续函数、可微函数的重要结论梳理 总结 在数学分析一中,关于闭区间上的连续函数,我们用区间套公理可获得一系列结论 区间套定理 ⇒ \Rightarrow ⇒ 有界性定理 ⇒ \Righta
数学分析复习:三角函数的周期性
文章目录 三角函数的周期性 本篇文章适合个人复习翻阅,不建议新手入门使用 三角函数的周期性 本节的主题是研究三角函数的周期性,我们之前已经解析地定义三角函数为 cos x = ∑ k = 0 ∞ ( − 1 ) k x 2 k ( 2 k ) ! , sin x = ∑ k = 0 ∞ ( − 1 ) k x 2 k + 1 ( 2 k + 1 ) ! \cos
数学分析复习:中值定理、反函数定理
文章目录 中值定理反函数定理 本篇文章适合个人复习翻阅,不建议新手入门使用 中值定理 定理:Rolle(罗尔)中值定理 设实值函数 f ∈ C 0 [ a , b ] f\in C^0[a,b] f∈C0[a,b] 且在 ( a , b ) (a,b) (a,b) 上可微,若 f ( a ) = f ( b ) f(a)=f(b) f(a)=f(b),则存在 x
数学分析复习:圆周率和 Euler 常数的构造
文章目录 圆周率 π \pi π 和 Euler 常数 e e e 的构造圆周率 π \pi π 的构造Euler常数e的构造 本篇文章适合个人复习翻阅,不建议新手入门使用 圆周率 π \pi π 和 Euler 常数 e e e 的构造 圆周率 π \pi π 的构造 我们将以下数列的极限定义为 π \pi π L n = n ⋅ sin 18 0
数学分析教程 第十七章学习感受
这一章讲傅里叶分析,这总该是我们学通信的强项了吧。不过很多基础性问题其实我也是不明白的。周期函数总可以展开成傅里叶级数,但是展开后是否收敛,如果收敛能否逐项求导、逐项积分等等。这便是级数问题的研究思路。 按照柯西的定义,傅里叶级数收敛的条件是原函数分段可微;特别的,如果连续则收敛于f(x)。但是柯西定义的收敛的概念太强了,以至于很多我们觉得似乎应该收敛的级数,并不收敛,比如-1的n次方求和。于
数学分析教程 第十六章学习感受
这一章专门讲反常积分。主要分为两大类:无穷积分与瑕积分。 无穷积分的理论与级数是平行的,柯西收敛原理,比较判别法,dirichlet判别法和abel判别法,甚至连abel求和公式都有对应的第二积分平均值定理。 瑕积分的判别可以通过变量代换变为一个无穷积分,也有等价的比较判别法。这里还提了beta函数和gamma函数,算是为了给含参变量的积分打一点基础吧。这里还提了一下柯西主值。 本章还
数学分析书籍(2024.02.19)
1、数学分析应该这样学(2023.05) 2、普林斯顿数学分析读本(图灵出品)-2020.08 3、数学分析概论 岩波定本+普林斯顿数学分析读本(套装2册) 4、数学分析八讲(修订版)(图灵出品) 5、数学分析十讲(2021.12) 6、普通高等学校“十二五”规划教材 数学分析选讲(2020.01) 7、数学
PTA模拟+数学分析
作者 李曲 单位 浙江工业大学 生物学家发现了一种奇怪的DNA分子,最好用集合{A,B}中的N个字符序列来描述。一个不太可能的突变序列导致了一条由A‟s组成的DNA链。生物学家发现这很奇怪,所以他们开始更详细地研究突变。 他们发现了两种类型的突变。一种类型导致改变序列的单个字符(A→B还是B→A) 。第二种类型更改序列的整个前缀,特别是用另一个字符(A替换B,B替换A)替换从1到K位置的所有