漫步数学分析十八——紧集上连续函数的有界性

本文主要是介绍漫步数学分析十八——紧集上连续函数的有界性，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

现在我们证明连续实值函数的一个重要性质，即有界定理。有界定理表明连续函数在紧集上是有界的并且在集合上的某些点取得最大值与最小值，准确的描述放到定理5中。

为了理解上面的结论，我们考虑非紧集上函数会发生什么情况。首先，连续函数不一定是有界的，图 $\ref{fig:4-5}$ 给出的是开区间 $(0,1)$ 上的函数 $f(x)=1/x$ ，随着 $x$ 越来越靠近0，函数变得任意大，但是不管怎样 $f$ 是连续的，因为 $f$ 是1 与连续函数 $x\mapsto x$ 的商，而这个连续函数在 $(0,1)$ 上不等于0。

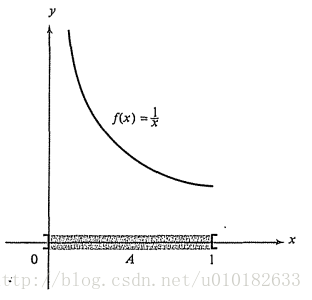
图1

接下来，我们将说明即便函数是有界且连续的，在其定义域内也可能没有最大值。图 $\ref{fig:4-6}$ 给出的是开区间 $[0,1)$ 上的函数 $f(x)=x$ ，这个函数没有最大值，因为即便有无限个点靠近1，但是没有任何一个点 $x$ 满足 $f(x)=1$ 。从这些例子中可以看出，对于紧集上的连续函数，这些情况都是不会发生的。

现在我们形式化成定理。

图2

$\textbf{定理5}$ 令 $A\subset R^n,f:A\to R$ 是连续函数，令 $K\subset A$ 是紧集，那么 $f$ 在 $K$ 上是有界的，即 $B=\{f(x)|x\in K\}\subset R$ 是有界集。进一步，存在点 $x_0,x_1\in K$ 使得 $f(x_0)=\inf(B),f(x_1)=\sup(B)$ ，我们称 $\sup(B)$ 是 $f$ 在 $K$ 上的最大值， $\inf(B)$ 是 $f$ 在 $K$ 上的最小值。

相比我们在微积分中学到的利用求导来定位极大值与极小值，这个结论要更近一步。例如 $R$ 上的一些处处不可导的连续函数；这样的函数我们无法用光滑曲线画出来，所以直观上不很明显。

$\textbf{例1：}$ 给出一个紧集上不连续函数的实例，且这个函数无界。

$\textbf{解：}$ 将 $f:[0,1]\to R$ 定义成：如果 $x>0,f(x)=1/x$ ，如果 $x=0,f(0)=0$ ，很明显这个函数与 $(0,1]$ 上的函数 $1/x$ 具有同样的无界性。

$\textbf{例2：}$ 对 $[0,1]$ 上的函数 $f(x)=x/(x^2+1)$ ，验证定理5。

$\textbf{解：}$ $f(0)=0,f(1)=1/2$ ，我们将验证它的最大值在 $x=1$ 处，最小值在 $x=0$ 处。首先，因为 $x\geq 0,x^2+1\geq1$ ，所以 $x/(x^2+1)\geq 0$ ，对于 $0\leq x\leq 1,f(x)\geq f(0)$ ，因此0是最小值。接下来，注意到 $0\leq(x-1)^2=x^2-2x+1$ ，所以 $x^2+1\geq 2x$ ，故当 $\neq 0$ 时，