漫步专题

HDU 1428 漫步校园（搜索 + dp）

OJ题目：click here ~~ 题意分析：题目中有句话“他考虑从A区域到B区域仅当存在一条从B到机房的路线比任何一条从A到机房的路线更近(否则可能永远都到不了机房了…)。”，关键是对这句话的理解。此刻在A区域，选择下面要走的B区域的条件是，存在一条B区域到机房的路线比A区域到机房的所有路线都近，也就是说，存在一条B区域到机房的路线比A区域到机房的最短路线更近（比最短的近

hdu（1273）漫步森林

本题考查了一个数学公式： n个点则有n*(n-1)/2个点，每次都需要走n条线，则共走（n-1)/2次；； #include"stdio.h"#include"string.h"int main(){int m;while(scanf("%d",&m),m){printf("%d\n",(m-1)/2);}return 0;}

【2023百度之星初赛】跑步，夏日漫步，糖果促销，第五维度，公园，新材料，星际航行，蛋糕划分

目录题目：跑步思路：题目：夏日漫步思路：题目：糖果促销思路：题目：第五维度思路：题目：公园思路：新材料思路：星际航行思路：题目：蛋糕划分编辑思路：题目：跑步小度每天早上要和小猫一起跑步。小猫的位置数值越小表示越在后面，速度越小表示越慢，它们都向一个方

hdu_1428 漫步校园

原题链接：http://acm.hdu.edu.cn/showproblem.php?pid=1428 分析：(属于简单的综合题，最短路（图论）+记忆化搜索（DP）) 由“他考虑从A区域到B区域仅当存在一条从B到机房的路线比任何一条从A到机房的路线更近(否则可能永远都到不了机房了…)” 知道，先要求出每个点到终点的最短路径。接着DFS得到可以满足条件的路径个数

云中漫步-旅行到宇宙边缘

大家好，我是阿飞云怕什么真理无穷，进一步有近一步的欢喜把小孩哄睡下了，坐在了书桌前，已经23:30半了，继续开始写自己这一周的云中漫步。夜晚是安静的，也是令人放松的。今天周六了，天终于晴了，延续了几日来一直是阴雨绵绵，我这一周也几乎天天在加班，赶一些工作的进度，顺便体验一把“996”，还真是有点吃不消，每天搞到快凌晨，回到家睡意全无，可能是过了之前睡觉的生物钟，躺下很久还不能入睡，感觉睡

云中漫步-我这一辈子

大家好，我是阿飞云怕什么真理无穷，进一步有近一步的欢喜云中漫步周末好啊，一大早，还没起床就听到窗外，就听到窗外滴滴答答的雨声。起床后打开窗户，外面的风吹进来，透着一丝丝的凉意。看着窗外树木也长出了许多新叶新芽，在雨水冲刷后格外翠绿。没有春天的长沙，继续开启属于它的雨季。我也开启了属于我的云中漫步，这是第一篇。我非常向往云中漫步的这一种状态，悠闲、洒脱，没有目的，很享受的随意走动。但

漫步云端之初读Google三大论文（一）

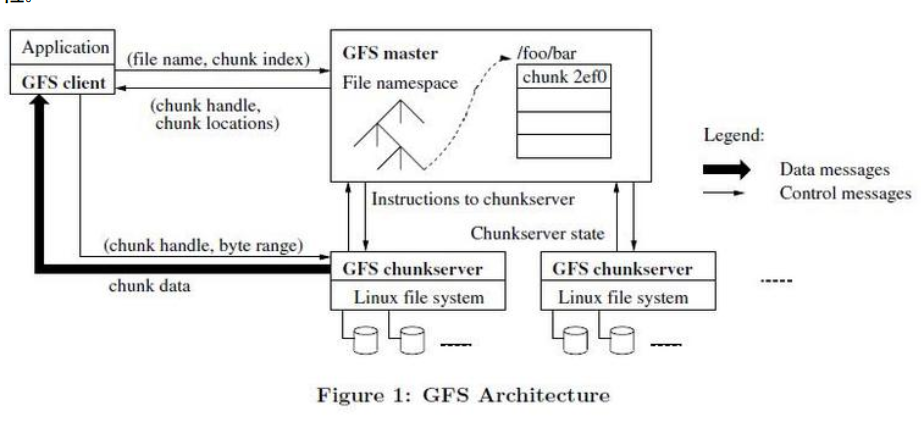
GFS(Goole File System)：对大数据时代的存储需求进行重新设计的分布式文件系统。背景：google迅速增长的业务和数据处理需求设计目标： - 性能 - 可伸缩性 - 可靠性 - 可用性以上设计目标与传统的分步式文件系统相同。关键在于不同点。不同之处： - 组建失效为常态 - 文件巨大 - 绝大部分文件的修改采用在文件尾部追加数据的方式，而非覆盖。

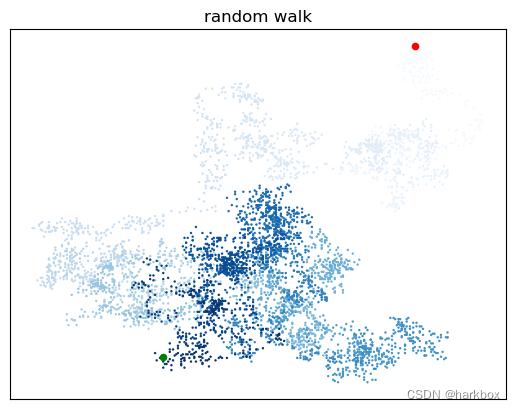
数据可视化训练第一天（matplotlib直线；散点图，随机漫步）

前言本人自己的练习记录；如有错误请指正； https://matplotlib.org/stable/gallery/lines_bars_and_markers/index.html 官方有许多例子，可以找到自己需要的图像模仿进行绘制 1.一个简单的直线例子就如同我们学习C语言的第一个helloword时候一样；我们也了解最基本的例子；关于具体细节可以不需要第一时间了解 import

漫步线性代数四——矩阵符号和矩阵乘法

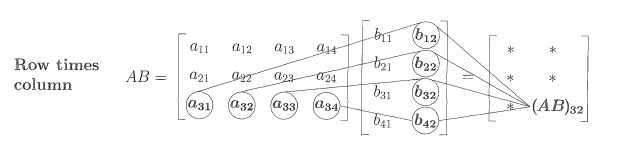
对于 3×3 3\times 3的例子，我们能够写出所有的公式。可以列出消去步骤，一个方程减去另一个方程的倍数达到三角矩阵的形式。对于一个大的系统，这种跟踪消去的步骤太长了，所以我们需要更加简洁的记录方式。我们现在引进矩阵符号来描述开始的系统，用矩阵乘法来描述计算步骤会更简单。注意三种不同类型的量都出现在例子中： Nine coefficientsThree unknownsThre

漫步微积分二十一——不定积分和换元法

如果 y=F(x) y=F(x)是导数已知的函数，例如 ddxF(x)=2x(1) \begin{equation}\frac{d}{dx}F(x)=2x\tag1\end{equation}我们能够知道函数 F(x) F(x)？不需要多想我们就能写出符合要求的函数，即 F(x)=x2 F(x)=x^2。更进一步，添加一个常数不会改变导数结果，所以下面的所有函数

漫步微积分十六——最大最小值问题

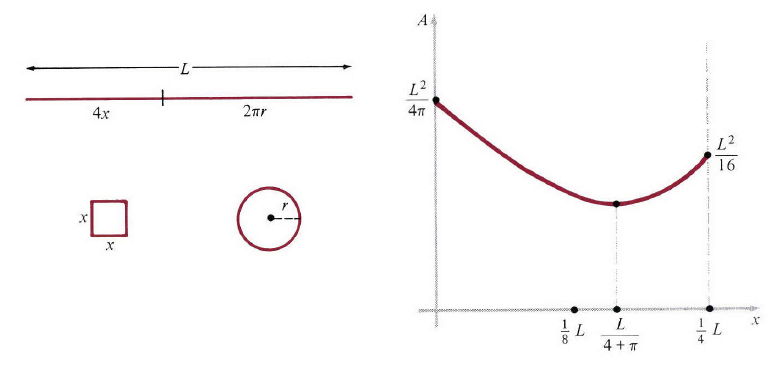
微积分最引人注目的应用就是寻找函数的最大或最小值或者需要用到最大和最小值。日常生活充满了这样的问题，数学家和其他人觉得它们很有趣也非常重要。一个商人旨在使利润最大化和成本最小化。工程师设计的新汽车希望其效率最大化。航空公司飞行员希望减少飞行时间和燃料消耗。在科学中，我们经常发现自然以某种方式在最大化或最小化某一量。例如，一缕光线穿过透镜，总是沿着时间最短的那条路径。挂链最终的形状其重力势能最小

漫步微积分九——乘法和除法法则

上篇文章中，我们学习了如何对和函数，差函数和常数乘函数进行求导。现在考虑 products uvquotions uv. products\ uv\quad quotions\ \frac{u}{v}. 其中 u,v u,v可以看作对 x x可导的函数。因为和的导数时导数的和，自然而然我们猜想，乘积的导数可能等于导数的乘积。然而，通过一个简单的例子我们就看出这个猜想不正确。

漫步微积分八——多项式求导

微分学有其自身的独特性和重要性，已被应用到物理、生物和社会科学中。它能够快速渗入到应用中，并得到问题的核心。然而，从整体效率的角度看，它的具体内容推迟一下，我们先花一点时间学习如何快速而准确的求导。我们已经知道，对函数求导的过程称作微分。这个过程直接依赖于导数的极限定义， f ′ ( x ) = lim ⁡ Δ x → 0 f ( x + Δ x ) − f ( x ) Δ x , f&#x

漫步微积分四——导数的定义

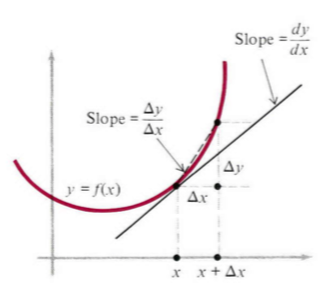
从几何上考虑，我们利用上一篇博文中的(8)，并丢掉下标 x0 x_0，就得到导数的基本定义：给定任意函数 f(x) f(x)，导数 f′(x) f'(x)是新的函数，在点 x x处的值定义为 f′(x)=limΔx→0f(x+Δx)−f(x)Δx(1)\begin{equation}f'(x)=\lim_{\Delta x\to 0}\frac{f(x+\Delta x)-f(x)}{\Del

漫步微积分三——如何计算切线的斜率

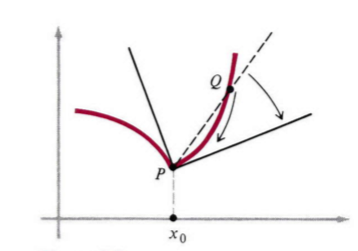
各种想法都有自己的一席之地，但是时间会剔除许多细节。 P＝(x0,y0) P＝(x_0,y_0)是抛物线 y＝x2 y＝x^2上的任意一个定点，如图1所示。作为基本思想的第一个图例，给定抛物线上一点 P P，计算切线的斜率。首先，我们选择曲线上的一个临近点Q=(x1,y1)Q=(x_1,y_1)。接下来，我们画出由这两点确定的割线 PQ PQ，割线的斜率明显是： msec=slope o

漫步数学分析十四——连通集

定义3 \textbf{定义3} 集合 A⊂Rn A\subset R^n为连通集，如果不存在两个非空开集 U,V U,V，使得 A⊂U∪V,A∩U≠∅,A∩V≠∅,A∩U∩V=∅ A\subset U\cup V,A\cap U\neq\emptyset,A\cap V\neq\emptyset,A\cap U\cap V=\emptyset。直观上，集合 U,V U,V将 A A分成了两

在给出 Rn R^n中紧集的精确定义前，我们需要介绍一些术语。对于集合 A⊂Rn A\subset R^n，当且仅当存在一个常数 M≥0 M\geq0使得 A⊂D(0,M) A\subset D(0,M)，那么就称该集合是有界的(bounded)，所以一个集合被邻域原点的某个邻域 D(0,M) D(0,M)包住时，它就是有界的；换句话说，对于所有的 x∈A,∥x∥<M x\in A,\Vert x

漫步数学分析五——闭集

定义3 \textbf{定义3} 对于 Rn R^n中的集合 B B，如果它在RnR^n中的补(即集合 Rn∖B R^n\backslash B)是开集，那么它是闭集。例如，单点是闭集，含有边界的单位圆组成的集合是闭集。大致来说，当集合包含它的边界点时它就是闭的(直观感觉可从图6中看出)，如图1所示。图1 存在既不是开集又不是闭集的集合。例如在 R1 R^1，中半

漫步数学分析三——开集

为了定义开集，我们首先介绍 ε−disc \varepsilon-\text{disc}的概念。定义1 \textbf{定义1} 对于每个固定的 x∈Rn x\in R^n以及 ε>0 \varepsilon>0，集合 D(x,ε)={y∈Rn|d(x,y)<ε} D(x,\varepsilon)=\{y\in R^n|d(x,y)<\varepsilon\} 称为关

漫步凸分析十一——分离定理

令 C1,C2 C_1,C_2是 Rn R^n中的非空集合，有一个超平面 H H，如果C1C_1含于其中的一个闭半空间而 C2 C_2含于相对立的闭半空间，那么我们称 H H分离(separate)C1,C2C_1,C_2；如果 C1,C2 C_1,C_2 都不含于 H H，那么我们成HH真(properly)分离 C1,C2 C_1,C_2；如果存在 ε>0 \varepsilon>0使得 C1

漫步凸分析四——凸函数

令函数 f f的值域是实数或±∞\pm\infty，定义域是 Rn R^n的一个子集，集合 {(x,μ)|x∈S,μ∈R,μ≥f(x)} \{(x,\mu)|x\in S,\mu\in R,\mu\geq f(x)\} 叫做 f f的上境图(epigraph)，用epiff表示，如果epi f f是Rn+1R^{n+1}的凸子集，那么我们将 f f定义为凸函数。对于SS 上

漫步微积分三十二——两条曲线间的面积

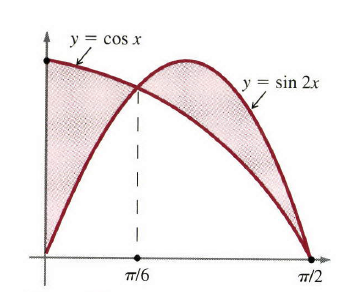
假设我们给出了两条曲线 y=f(x),yg(x) y=f(x),yg(x)，如图1所示，在 x=a,b x=a,b处有交点并且在区间 [a,b] [a,b]内第一条曲线位于第二条的上方，为了求出曲线之间的面积，很自然地想法是使用如图所示垂直的细条。在 x x处的高度为低点的曲线与高点之间的距离f(x)−g(x)f(x)-g(x)，其底是 dx dx。因此，面积的单元是 dA=[f(x)−

漫步微积分二十八——极限思想下的面积计算

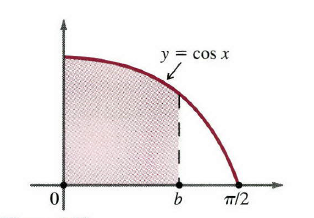
上篇文章中讨论的概念给出了计算面积的实际过程。现在我们利用一些实例来测试这个过程是如何工作的。例1：考虑区间 [0,b] [0,b]上的函数 y=f(x)=x y=f(x)=x。图像(图1)下面的区域是高和底都为 b b的矩形，所以它的面积明显是b2/2b^2/2。然而，我们需要去证实我们极限过程给出相同的答案，更重要的是，理解立即过程如何给出答案。图1 n n是

漫步数学分析三十九——隐函数定理

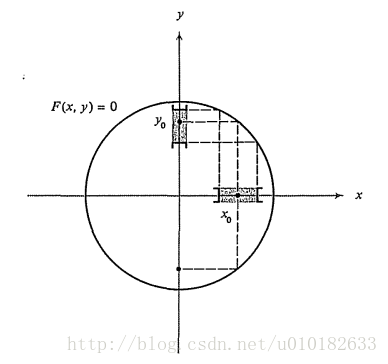
假设 x,y x,y被方程 F(x,y)=0 F(x,y)=0关联起来，我们会说这定义了一个函数 y=f(x) y=f(x)(或者说隐式定义了 y=f(x) y=f(x))，然后打算计算 dy/dx dy/dx。前面已经提到过，给定这样的 F F，一般不能显式求出yy，所以在没有求解之前知道这样的函数存在是非常重要的。为了更好的理解给出的结论，考虑函数 F(x,y)=x2+y2−1 F(x,y

漫步数学分析三十六——泰勒定理

我们讨论一般函数 f:A⊂Rn→Rm f:A\subset R^n\to R^m的泰勒公式，为此我们首先讨论高阶导数。对于 f:Rn→R f:R^n\to R，定义高阶偏导没有问题；我们仅仅迭代偏导的过程 ∂2f∂x1∂x2=∂∂x1(∂∂x2f) \frac{\partial^2f}{\partial x_1\partial x_2}=\frac{\partial}{\parti

漫步数学分析三十五——均值定理

我们现在考虑两个非常重要的定理，也就是均值定理与泰勒(Taylor)定理。首先，我们考虑均值定理，我们先回顾一下基本微积分中的均值定理，如果 f:[a,b]→R f:[a,b]\to R是连续的，在 (a,b) (a,b)上可微，那么存在点 c∈(a,b) c\in(a,b)使得 f(b)−f(a)=f′(c)(b−a) f(b)-f(a)=f^\prime(c)(b-a)，其中 f′=df/dx