漫步数学分析三十五——均值定理

本文主要是介绍漫步数学分析三十五——均值定理，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

我们现在考虑两个非常重要的定理，也就是均值定理与泰勒(Taylor)定理。首先，我们考虑均值定理，我们先回顾一下基本微积分中的均值定理，如果$f:[a,b]\to R$是连续的，在$(a,b)$上可微，那么存在点$c\in(a,b)$使得$f(b)-f(a)=f^\prime(c)(b-a)$，其中$f^\prime=df/dx$。

不幸的是，对于$f:A\subset R^n\to R^m$而言，这个均值定理不为真。例如考虑$f:R\to R^2$，其定义为$f(x)=(x^2,x^3)$，我们现在试着找出$c$使得$0\leq c\leq 1$并且$f(1)-f(0)=Df(c)(1-0)$，这就意味着$(1,1)-(0,0)=(2c,3c^2)$，从而$2c=1,3c^2=1$，很显然不存在满足这些等式的$c$。

经验启发我们应该还需要一些限制条件，这样的话为了使得上面的版本正确，$f$必须是实值函数，为了得到正确的定理我们首先精确定义对$c,x,y\in R^n$而言$c$在$x,y$之间是什么意思。

我们说$c$位于连接$x,y$的线段上或在$x,y$之间，如果存在$0\leq\lambda\leq1$使得$c=(1-\lambda)x+\lambda y$，如图1

图1

$\textbf{定理7}$
$\textrm{(i)}$假设$f:A\subset R^n\to R$在开集$A$上可微，对于使得$x,y$之间的线段位于$A$中的任意$x,y\in A$，存在点$c$位于那条线段上使得

$$f(y)-f(x)=Df(c)(y-x)$$

$\textrm{(ii)}$假设$f:A\subset R^n\to R^m$在开集$A$上可微，假设连接$x,y$的线段位于$A$中并且$f=(f_1,\ldots,f_m)$，那么在那条线段上存在点$c_1,\ldots,c_m$使得

$$f_i(y)-f_i(x)=Df_i(c_i)(y-x),\quad i=1,\ldots,m$$

$\textbf{例1：}$对于集合$A\subset R^n$，如果对每个$x,y\in A$，连接他们的线段也位于$A$中，那么该集合称为凸集，如图$\ref{fig:6-12}$所示。令$A\subset R^n$是开凸集并且$f:A\to R^m$是可微的，如果$Df=0$，那么说明$f$是常数。

$\textbf{解：}$对于$x,y\in A$，对于每个元素$f_i$，我们有向量$c_i$使得

$$f_i(y)-f_i(x)=Df_i(c_i)(y-x)$$

因为对于每个$i,Df=0,Df_i=0$所以$f_i(y)=f_i(x)$，从而$f(y)=f(x)$，这就意味着$f$是常数。

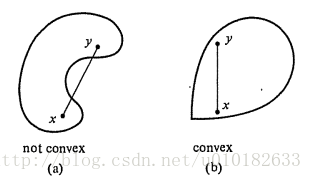
图2

$\textbf{例2：}$假设$f:[0,\infty]\to R$是连续的，$f(0)=0$，$f$在$(0,\infty)$上可微且$f^\prime$是非减的，证明对于$x>0$而言$g(x)=f(x)/x$是非减的。

$\textbf{解：}$从均值定理我们可以看出如果函数$h$的$h^\prime(x)\geq 0$，那么$h$是非减的，因为$x\leq y$意味着

$$h(y)-h(x)=h^\prime(c)(y-x)\geq0$$

接下来

$$g^\prime(x)=\frac{xf^\prime(x)-f(x)}{x^2}$$

并且

$$f(x)=f(x)-f(0)-f^\prime(c)\cdot x\leq xf^\prime(x)$$

因为$0<c<x,f^\prime(x)\geq f^\prime(c)$，从而$xf^\prime(x)-f(x)\geq 0$，所以$g^\prime\geq0$，这就意味着 g <script type="math/tex" id="MathJax-Element-3542">g</script>是非减的。

博文pdf版本下载地址：http://pan.baidu.com/s/1nv7D7rN

这篇关于漫步数学分析三十五——均值定理的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---