漫步微积分三十二——两条曲线间的面积

本文主要是介绍漫步微积分三十二——两条曲线间的面积，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

假设我们给出了两条曲线$y=f(x),yg(x)$，如图1所示，在$x=a,b$处有交点并且在区间$[a,b]$内第一条曲线位于第二条的上方，为了求出曲线之间的面积，很自然地想法是使用如图所示垂直的细条。在$x$处的高度为低点的曲线与高点之间的距离$f(x)-g(x)$，其底是$dx$。因此，面积的单元是

$$dA=[f(x)-g(x)]dx$$

总面积为

$$\begin{equation} A=\int dA=\int_a^b[f(x)-g(x)]dx\tag1 \end{equation}$$

我们将较小的$a$设为积分下限，将$b$设为上限来计算积分值。这样的话增量(或者说微分)$dx$将一直是正的。另外还应该指出，当$x=a,b$时，两个函数产生相同的$y$值；也就是说，他们是方程$f(x)=g(x)$的解。为了找到它们，我们需要求解这个方程。

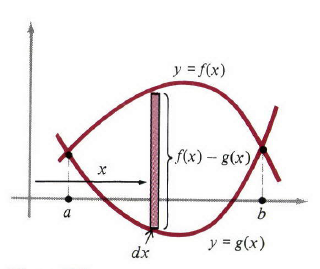
图1

我们建议大家不要靠死记硬背记住公式(1)，并且机械的将它套用到面积问题上。我们的目标是掌握这个方法，利用几何思想与对问题从无到有的构造出所需公式都是为了达到这个目标。该方法同样适用于水平窄带，往往这样做会更方便。在这种情况下，窄带的宽度将是$dy$，总面积将通过对$y$积分得到。

作为大家的辅助手段，对用积分求面积的方法，我们列出了它所遵循的大纲：

1. 画出要求的面积区域，在图上写下边界曲线的方程并找到他们的交点。
2. 确定用垂直窄带(宽为$dx$)还是水平窄带(宽为$dy$)，在图中画出一条窄带。
   • 着图像并利用曲线边界的方程，写下窄带面积$dA$，也就是长和宽的乘积。将$dA$完全用变量($x$ 或$y$)表示出来。
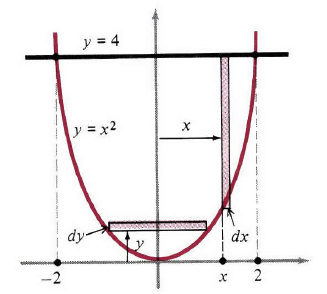
   • 在$x$或$y$的上下限之间积分$dA$，上下限可以通过检查图像得到。

   • 例1：曲线$y=x^2,y=4$的边界围成的区域如图2所示，如果我们选用垂直窄带，那么它的长度为$4-x^2$，面积为$dA=(4-x^2)dx$。整个区域的面积为
     

     $$\begin{align*} \int_2^2(4-x^2)dx &=4x-\frac{1}{3}x^3\big|_{-2}^2\\ &=(8-\frac{8}{3})-(-8+\frac{8}{3})=\frac{32}{3} \end{align*}$$

     我们建议大家尽可能使用对称来简化计算。在这种情况下，图像左右对称，所以我们只需计算从$x=0$到$x=2$之间的积分，它是面积的一半，然后乘以2就得到总面积：
     

     $$2\int_0^2(4-x^2)dx=2(4x-\frac{1}{3}x^3)\big|_{0}^2=2(8-\frac{8}{3})=\frac{32}{3}$$

     正如计算展示的那样，这样做有一个好处，就是一个积分的极限是0。
     

     
     
     图2
     

     如果我们决定用水平窄带，那么长度就是右端的$x$值减去左端的$x$值。即$\sqrt{y}-{-\sqrt{y}}$，所以$dA=[\sqrt{y}-(-\sqrt{y})]dy=2\sqrt{y}dy$，整个面积是
     

     $$\int_0^42\sqrt{y}dy=\frac{4}{3}y^{3/2}\Big|_0^4=\frac{32}{3}$$

     答案跟以前一样，这并不奇怪，但不管这样令人放心。

     我们曾经强调过好的图像对理解以及执行这些过程是多么重要。

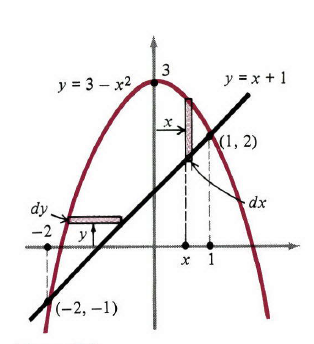
     例2：曲线$y=3-x^2,y=x+1$的边界围成的区域如图3所示。通过求解方程可以很快求出交点，利用$y$值相等得
     

     $$\begin{align*} 3-x^2&=x+1\\ x^2+x-2&=0\\ (x+2)(x-1)&=0\\ x&=-2,1 \end{align*}$$

     交点是$(-2,-1),(1,2)$。垂直窄带的长度为$(3-x^2)-(x+1)=2-x^2-x$，所以区域的面积可以通过求积分$dA=(2-x^2-x)$得到，上下限是$-2,1$
     

     $$\begin{align*} \int_{-2}^1((2-x^2-x)dx &=(2x-\frac{1}{3}x^3-\frac{1}{2}x^2)\big|_{-2}^1\\ &=(2-\frac{1}{3}-\frac{1}{2})-(-4+\frac{8}{3}-2)=4\frac{1}{2} \end{align*}$$

     在这个问题中，使用水平窄带比较麻烦，因为如果$y<2$，水平窄带显然是从抛物线左半部分到达到直线的，如果$y>2$，它是从抛物线左半部分到右半部分，这意味着$dA$必须根据$y<2$还是$y>2$使用不同的公式。
     

     
     
     图3
     

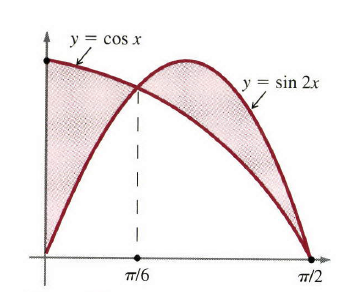
     例3：求出曲线$y=\cos x,y=\sin 2x$ 在区间$0\leq x\leq \pi/2$上围成的区域面积。

     解：曲线如图4所示，面积由两个阴影部分组成。这个例子的主要特征是曲线互相交叉，所以开始是第一个曲线在上面，然后是第二个。为了求解它，我们首先需要求出交点，这就意味着我们需要求解方程$\cos x=\sin x$。
     

     $$\cos x=2\sin x\cos x,\quad \sin x=\frac{1}{2}\quad x=\frac{\pi}{6}$$

     据此
     

     $$dA= \begin{cases} (\cos x-\sin 2x)dx\quad for\ 0\leq x\leq \frac{\pi}{6}\\ (\sin 2x-\cos x)dx\quad for\ \frac{\pi}{6}\leq x\leq \frac{\pi}{2} \end{cases}$$

     因此所求的面积为
     

     $$\begin{align*} \int_0^{\pi/6}(\cos &x-\sin 2x)dx+\int_{\pi/6}^{\pi/2}(\sin 2x-\cos x)dx\\ &=(\sin x+\frac{1}{2}\cos 2x)\Big|_0^{\pi/6}+(-\frac{1}{2}\cos 2x-\sin x)\Big|_{\pi/6}^{\pi/2}\\ &=(\frac{1}{2}+\frac{1}{4}-0-\frac{1}{2})+(\frac{1}{2}-1+\frac{1}{4}+\frac{1}{2})=\frac{1}{2} \end{align*}$$
     
     
     
     图4
     

这篇关于漫步微积分三十二——两条曲线间的面积的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---