微积分专题
微积分-积分应用5.4(功)
术语“功”在日常语言中用来表示完成一项任务所需的总努力量。在物理学中,它有一个依赖于“力”概念的技术含义。直观上,你可以将力理解为对物体的推或拉——例如,一个书本在桌面上的水平推动,或者地球对球的向下拉力。一般来说,如果一个物体沿着一条直线运动,位置函数为 s ( t ) s(t) s(t),那么物体上的力 F F F(与运动方向相同)由牛顿第二运动定律给出,等于物体的质量 m m m 与其
微积分直觉:隐含微分
目录 一、介绍 二、梯子问题 三、结论 四、一个额外的例子 一、介绍 让我们想象一个半径为 5 的圆,以 xy 平面为中心。现在假设我们想在点 (3,4) 处找到一条切线到圆的斜率。 好吧,为了做到这一点,我们必须非常接近圆和切线之间的空间,并沿着该曲线迈出一小步。该步骤的 y 分量为 dy,x 分量为
分数阶微积分MATLAB计算
习题1 syms t z;Gam=int(exp(-t)*t^(z-1),t,0,inf);I1=subs(Gam,z,sym(1/2)),I2=subs(Gam,z,sym(3/2)),I3=subs(Gam,z,sym(5/2)),I4=subs(Gam,z,sym(7/2))
微积分复习笔记 Calculus Volume 1 - 1.2 Basic Classes of Functions
1.2 Basic Classes of Functions - Calculus Volume 1 | OpenStax
微积分复习笔记 Calculus Volume1 - 1.1 Review of Functions
1.1 Review of Functions - Calculus Volume 1 | OpenStax
数学基础 -- 微积分之三角函数幂的积分
三角函数幂的积分处理 1. 积分形式 1.1 ∫ sin m ( x ) cos n ( x ) d x \int \sin^m(x) \cos^n(x) \, dx ∫sinm(x)cosn(x)dx 1.1.1 当 n n n 为奇数时 分离奇数次幂 如果 cos n ( x ) \cos^n(x) cosn(x) 是奇数次幂,可以将其分解为 cos n −
Python算法工程师面试整理-微积分
1. 导数 ● 定义:导数表示函数的瞬时变化率。 ● 常用规则: ○ 乘法规则:(fg)' = f'g + fg'。 ○ 链式法则:(f(g(x)))' = f'(g(x))
数学基础 -- 微积分之近似误差计算
微积分中的近似误差 在微积分中,近似计算是常见的工具,特别是在数值分析中。近似中的误差通常可以分为截断误差(truncation error)和舍入误差(round-off error)。以下是这两种误差的详细解释: 1. 截断误差 当使用有限项的级数或某种近似方法来代替实际的函数或积分时,未使用的部分会引入误差。举例来说,在使用泰勒级数展开函数时,只取有限的几项,那么未展开的项就会带来截断
计算图上的微积分:Backpropagation
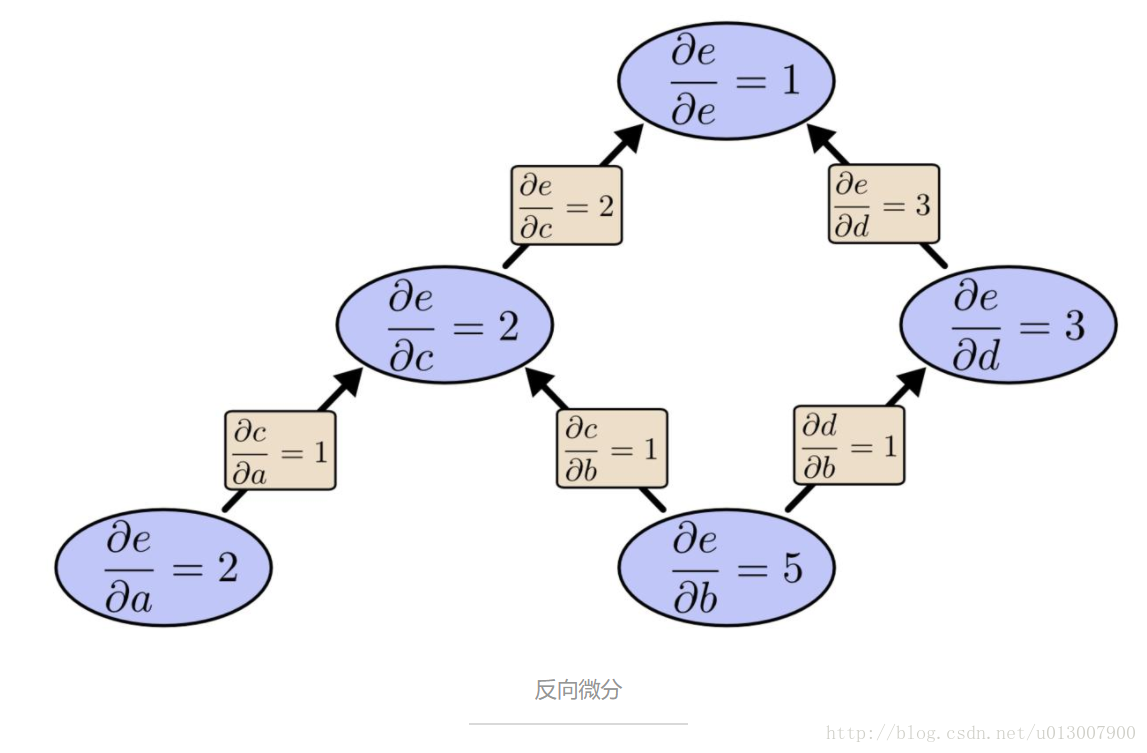
计算图上的微积分:Backpropagation 引言 Backpropagation (BP) 是使得训练深度模型在计算上可行的关键算法。对现代神经网络,这个算法相较于无脑的实现可以使梯度下降的训练速度提升千万倍。而对于模型的训练来说,这其实是 7 天和 20 万年的天壤之别。 除了在深度学习中的使用,BP 本身在其他的领域中也是一种强大的计算工具,例如从天气预报到分析数值的稳定性——只是
微积分-导数1(导数与变化率)
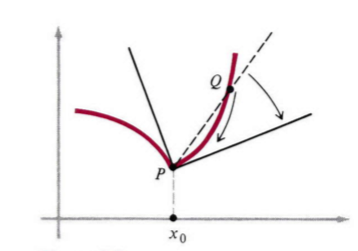
切线 要求与曲线 C C C相切于 P ( a , f ( a ) ) P(a, f(a)) P(a,f(a))点的切线,我们可以在曲线上找到与之相近的一点 Q ( x , f ( x ) ) Q(x, f(x)) Q(x,f(x)),然后求出割线 P Q PQ PQ的斜率: m P Q = f ( x ) − f ( a ) x − a m_{PQ} = \frac{f(x) - f(a)}
数学基础——微积分在机器/深度学习上的应用
目录 微分学 导数 偏导数 梯度 梯度下降算法 反向传播算法 自动求导 计算图 正则化与过拟合 L1正则化 L2正则化 Dropout正则化 拉格朗日对偶问题 拉格朗日乘数法 凸优化 对偶问题 KKT条件 Slater条件 积分学 笔记内容 微积分是17世纪后半叶发展起来的数学的一个分支。微积分有两个分支:微分学和积分学。 微分学
从“微积分”角度--话谈“芝诺悖论-阿基里斯与龟”
阿基里斯(又名阿喀琉斯)是古希腊神话中善跑的英雄。在他和乌龟的竞赛中,他速度为乌龟十倍,乌龟在前面100米跑,他在后面追,但他不可能追上乌龟。因为在竞赛中,追者首先必须到达被追者的出发点,当阿喀琉斯追到100米时,乌龟已经又向前爬了10米,于是,一个新的起点产生了;阿喀琉斯必须继续追,而当他追到乌龟爬的这10米时,乌龟又已经向前爬了1米,阿喀琉斯只能再追向那个1米。就这样,乌龟会制造出无穷个起点,
中国数学老师在 P 站上教微积分,年入 170 万?!…网友:看不懂,但我悟了!
这是「进击的Coder」的第 174 篇热点新闻 来源:北美留学生日报 | 英国那些事儿(hereinuk) “ 阅读本文大概需要 6 分钟。 ” 哪里是教微积分最好的地方?对来自中国台湾省的数学老师张旭来说, 不是个人网站、不是油管、不是在线辅导课,也不是线下补课班, 而是,P 站。 在这个全球知名的 se 情网站上,赵旭老师穿着朴素的卫衣,戴着粗黑框眼镜,讲了 226 堂微积分课, 时
AI算法工程师课程学习-数学基础-高数1-微积分
机器学习数学基础学习路线:1.高中数学-->大学2.微积分-->3.线性代数-->4.概率论-->5.优化理论。 为尽快进入到AI算法课程的学习,现在高数的学习要求: 1.看得懂,知道是什么,能听得懂,能理解讲的是什么;2.会查资料,例如通过市面上相关的AI工具来计算(省时省力),我也是第一次学AI算法工程师,我将数学基础部分的学习都记录下来,希望对走同样路的小伙伴们有些帮助。 1.微积
漫步微积分二十一——不定积分和换元法
如果 y=F(x) y=F(x)是导数已知的函数,例如 ddxF(x)=2x(1) \begin{equation}\frac{d}{dx}F(x)=2x\tag1\end{equation}我们能够知道函数 F(x) F(x)?不需要多想我们就能写出符合要求的函数,即 F(x)=x2 F(x)=x^2。更进一步,添加一个常数不会改变导数结果,所以下面的所有函数
漫步微积分十六——最大最小值问题
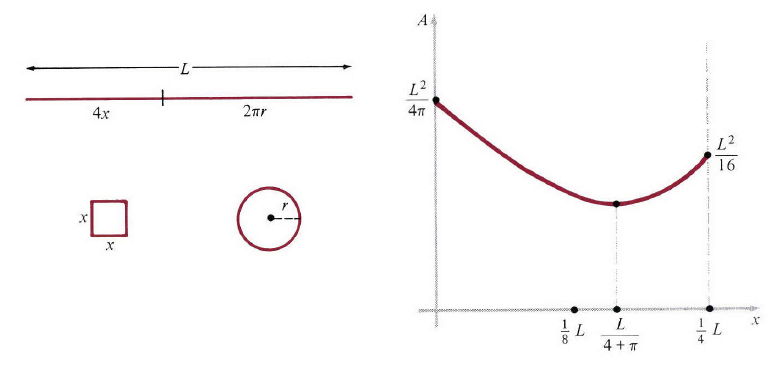
微积分最引人注目的应用就是寻找函数的最大或最小值或者需要用到最大和最小值。 日常生活充满了这样的问题,数学家和其他人觉得它们很有趣也非常重要。一个商人旨在使利润最大化和成本最小化。工程师设计的新汽车希望其效率最大化。航空公司飞行员希望减少飞行时间和燃料消耗。在科学中,我们经常发现自然以某种方式在最大化或最小化某一量。例如,一缕光线穿过透镜,总是沿着时间最短的那条路径。挂链最终的形状其重力势能最小
漫步微积分九——乘法和除法法则
上篇文章中,我们学习了如何对和函数,差函数和常数乘函数进行求导。现在考虑 products uvquotions uv. products\ uv\quad quotions\ \frac{u}{v}. 其中 u,v u,v可以看作对 x x可导的函数。因为和的导数时导数的和,自然而然我们猜想,乘积的导数可能等于导数的乘积。然而,通过一个简单的例子我们就看出这个猜想不正确。
漫步微积分八——多项式求导
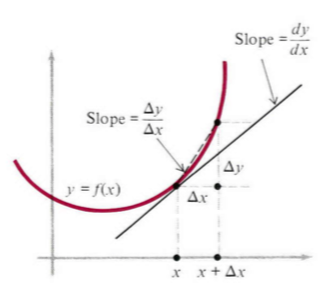
微分学有其自身的独特性和重要性,已被应用到物理、生物和社会科学中。它能够快速渗入到应用中,并得到问题的核心。然而,从整体效率的角度看,它的具体内容推迟一下,我们先花一点时间学习如何快速而准确的求导。 我们已经知道,对函数求导的过程称作微分。这个过程直接依赖于导数的极限定义, f ′ ( x ) = lim Δ x → 0 f ( x + Δ x ) − f ( x ) Δ x , f&#x
漫步微积分四——导数的定义
从几何上考虑,我们利用上一篇博文中的(8),并丢掉下标 x0 x_0,就得到导数的基本定义:给定任意函数 f(x) f(x),导数 f′(x) f'(x)是新的函数,在点 x x处的值定义为 f′(x)=limΔx→0f(x+Δx)−f(x)Δx(1)\begin{equation}f'(x)=\lim_{\Delta x\to 0}\frac{f(x+\Delta x)-f(x)}{\Del
漫步微积分三——如何计算切线的斜率
各种想法都有自己的一席之地,但是时间会剔除许多细节。 P=(x0,y0) P=(x_0,y_0)是抛物线 y=x2 y=x^2上的任意一个定点,如图1所示。作为基本思想的第一个图例,给定抛物线上一点 P P,计算切线的斜率。首先,我们选择曲线上的一个临近点Q=(x1,y1)Q=(x_1,y_1)。接下来,我们画出由这两点确定的割线 PQ PQ,割线的斜率明显是: msec=slope o
漫步微积分三十二——两条曲线间的面积
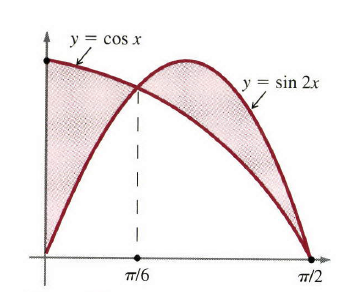
假设我们给出了两条曲线 y=f(x),yg(x) y=f(x),yg(x),如图1所示,在 x=a,b x=a,b处有交点并且在区间 [a,b] [a,b]内第一条曲线位于第二条的上方,为了求出曲线之间的面积,很自然地想法是使用如图所示垂直的细条。在 x x处的高度为低点的曲线与高点之间的距离f(x)−g(x)f(x)-g(x),其底是 dx dx。因此,面积的单元是 dA=[f(x)−
漫步微积分二十八——极限思想下的面积计算
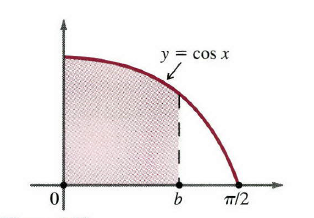
上篇文章中讨论的概念给出了计算面积的实际过程。现在我们利用一些实例来测试这个过程是如何工作的。 例1:考虑区间 [0,b] [0,b]上的函数 y=f(x)=x y=f(x)=x。图像(图1)下面的区域是高和底都为 b b的矩形,所以它的面积明显是b2/2b^2/2。然而,我们需要去证实我们极限过程给出相同的答案,更重要的是,理解立即过程如何给出答案。 图1 n n是
Python和MATLAB及C++资产价格看涨看跌对冲模型和微积分
🎯要点 🎯资产价格动态数学随机模型:🖊价格几何布朗运动过程积分 | 🖊布朗运动和几何布朗运动随时间概率密度 | 🖊几何布朗运动离散过程 | 🖊电动车历史股票价值及预期。🎯金融衍生品估值偏微分方程:🖊期权合约 | 🖊计算看涨期权期权面,显示对冲参数及预期价格 | 🖊计算看跌期权的期权面 | 🖊对冲看涨期权投资组合 | 🖊再平衡频率对投资组合方差的影响。🎯期权价格与隐含概率