漫步微积分三——如何计算切线的斜率

本文主要是介绍漫步微积分三——如何计算切线的斜率，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

各种想法都有自己的一席之地，但是时间会剔除许多细节。

$P＝(x_0,y_0)$是抛物线$y＝x^2$上的任意一个定点，如图1所示。作为基本思想的第一个图例，给定抛物线上一点$P$，计算切线的斜率。首先，我们选择曲线上的一个临近点$Q=(x_1,y_1)$。接下来，我们画出由这两点确定的割线$PQ$，割线的斜率明显是：

$$m_{sec}={\rm slope\ of} \ PQ=\frac{y_1-y_0}{x_1-x_0}\tag 1$$

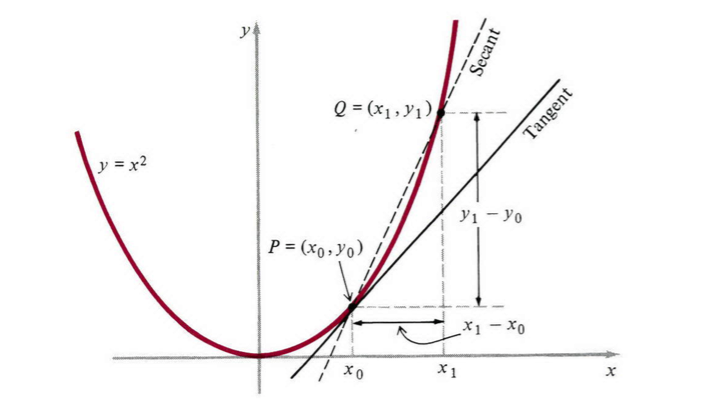图1

现在是关键的一步︰我们让$x_1$靠近$x_0$，以便点$Q$接近定点$P$，就像一串沿着线滑动的佛珠。这样的话，割线开始改变方向并明显接近$P$。而且，直观上来看，切线的斜率是割线斜率计算得到的极限值。用标准符号来表达就是:

$$m={\rm \lim_{Q\to P}}\ m_{sec}=\lim_{x_1\to x_0}\frac{y_1-y_0}{x_1-x_0}\tag 2$$ 缩略词“lim”且下方有“$x_1\to x_0$”读作“当$x1$趋向$x_0$，…的极限是”。

我们不能简单的设置$x_1=x_0$来计算极限值$m$，因为那样的话$y_1=y_0$并且给出了无意义的结果：

$$m=\frac{y_0-y_0}{x_0-x_0}=\frac{0}{0}$$ 我们必须将 $x_1$看做非常接近 $x_0$而有别于它。然而，当 $x_1$趋进 $x_0$时， $y_1-y_0$和 $x_1-x_0$变的非常小，他们商的极限值是多少并不清楚。

解决这个困难的办法是用曲线的方程。因为$P$和$Q$都落在曲线上，我们有$y_0＝x_0^2$和$y_1＝x_1^2$，所以（1）可以写成：

$$m_{sec}=\frac{y_1-y_0}{x_1-x_0}=\frac{x_1^2-x_0^2}{x_1-x_0}\tag 3$$ 分子变小的原因是它的一个因子包含分母。如果约掉这个公因子，得到： $$m_{sec}=\frac{y_1-y_0}{x_1-x_0}=\frac{x_1^2-x_0^2}{x_1-x_0}=\frac{(x_1-x_0)(x_1+x_0)}{x_1-x_0}=x_1+x_0$$ （2）式就变成： $$m=\lim_{x_1\to x_0}\frac{y_1-y_0}{x_1-x_0}=\lim_{x_1\to x_0}(x_1+x_0)$$ 现在明显的看到：当 $x_1$越来越接近 $x_0$时， $x_1+x_0$越来越接近于等式 $x_1+x_0=2x_0$。相应的： $$m=2x_0\tag 4$$ 是曲线 $y＝x^2$在点 $P(x_0,y_0)$处切线的斜率。

例1:点（1,1）和（-1/2,1/4）在抛物线$y＝x^2$（图2）上。根据（4），这些点切线的斜率是$m=2$，$m=-1$。用直线的点斜方程，两条切线明显有两个方程：

$$\frac{y-1}{x-1}=2\quad \frac{y-\frac{1}{4}}{x+\frac{1}{2}}=-1$$ 同样的， $$\frac{y-x_0^2}{x-x_0}=2x_0$$ 是点 $（x_0,x_0^2）$处的切线方程。

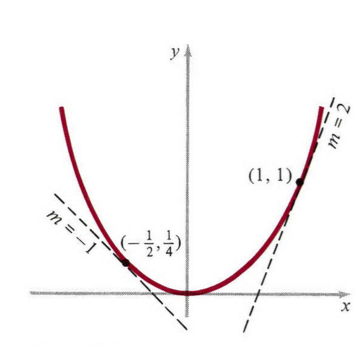
图2

现在我们介绍一个被广泛使用的符号，读作delta。

刚刚描述的过程从独立变量$x$的变化量开始。这种变化量的标准符号是$\Delta x$，所以

$$\Delta x=x_1-x_0\tag 5$$ 是 $x$从第一个值到第二个值的变化量。我们也可以将第二个值看成是第一个值加上变化量得到的： $$x_1=x_0+\Delta x\tag 6$$ $x$不是一个数$\Delta$和一个数 $x$的乘积，而是一个数，叫做$x$的增量。增量 $x$可以为正也可以为负。因此，如果$x_0=1，x_1=3$，那么 $x=3-1=2$；如果 $x_0=1，x_1=-2$，那么 $x=-2-1=-3$。

字母$\Delta$是希腊字母$d$；当它写在一个变量前面时，它表示该变量两个值之差。这个简单的符号是极为方便的，几乎扩展到数学和科学的每个部分。我们用它来重写上述计算过程。

将（5）或（6）带入（3）的：

$$m_{sec}=\frac{x_1^2-x_0^2}{x_1-x_0}=\frac{(x_0+\Delta x)^2-x_0^2}{\Delta x}\tag 7$$ 这一次没有分解分子，我们增加了它的第一项，化简得：

$$\begin{split}(x_0+\Delta x)^2-x_0^2 &=x_0^2+2x_0\Delta x+(\Delta x)^2-x_0^2\\ &=2x_0\Delta x+(\Delta x)^2\\ &=\Delta x(2x_0+\Delta x) \end{split}$$ 所以（7）变为： $$m_{sec}=2x_0+\Delta x$$ 如果我们将它带入（2），利用 $x_1\to x_0$等价于 $\Delta x\to 0$，我们发现： $$m=\lim_{\Delta x\to 0}(2x_0+\Delta x)=2x_0$$ 跟之前的结果一样。再次看到指定的极限过程发生了什么：随着 $x$越来越趋近于$0$， $2x_0+\Delta x$越来越趋近于 $2x_0$。

第二种方法（即使用delta符号）取决于扩大$(x_0+x)^2$，而第一种取决于分解表达式$x_1^2-x_0^2$。这种特定情况下，两种计算明显比其他方法容易。然而，第二种比第一种容易，为此我们采用增量作为我们的标准过程。

我们只进行了抛物线$y=x^2$的计算，理论上，任何函数$y=f(x)$（图3）都可以用此计算进行描述。我们首先计算通过两个点$P$和$Q$（对应于$x_0$和$x_0+x$）割线的斜率：

$$m_{sec}=\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$$ 然后计算 $x$趋进0时$m_{sec}$的极限，得到一个数 $m$，几何上它是曲线上点$P$割线的斜率： $$m=\lim_{\Delta x\to 0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$$ 这个极限值经常用 $f'(x_0)$表示，来强调它依赖于点 $x_0$和函数 $f(x)$。因此，根据定义我们有： $$f'(x_0)=\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x} \tag 8$$ 上面给出的计算结果也可以表示为：如果 $f(x)=x^2$，则 $f'(x_0)=2x_0$。

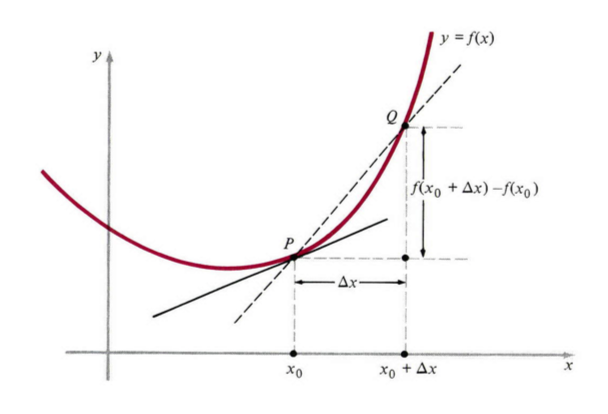
图3

例2:计算$f'(x_0)$ 其中$\quad f(x)=2x_2-3x$

解：（8）中的分子是：

$$\begin{align} f(x_0+\Delta x)-f(x_0)&=[2(x_0+\Delta x)^2-3(x_0+\Delta x)]-[2x_0^2-3x_0]\\ &=2x_0^2+4x_0\Delta x+2(\Delta x)^2-3x_0-3\Delta x-2x_0^2+3x_0\\ &=4x_0\Delta x+2(\Delta x)^2-3\Delta x\\ &=\Delta x(4x_0+2\Delta x-3) \end{align}$$ 因此（8）变为： $$\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}=\Delta x(4x_0+2\Delta x-3)$$ $$f'(x_0)=\lim_{\Delta x\to 0}\Delta x(4x_0+2\Delta x-3)=4x_0-3$$ 我们根据假设得到 (8)，即曲线有单一明确的切线。这的确是个假设，因为一些曲线并没有这种切线(图4)。然而，当切线存在时，它显然需要割线 $PQ$靠近极限位置，无论 $Q$是从右还是从左。这两种方法区别在于$x$靠近0时是只通过正值还是只通过负值。当极限存在时，两个方向靠近得到的极限值相同，这是（8）含义的一部分。

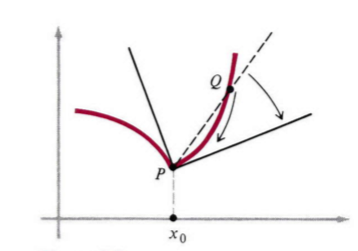
图4

这篇关于漫步微积分三——如何计算切线的斜率的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---