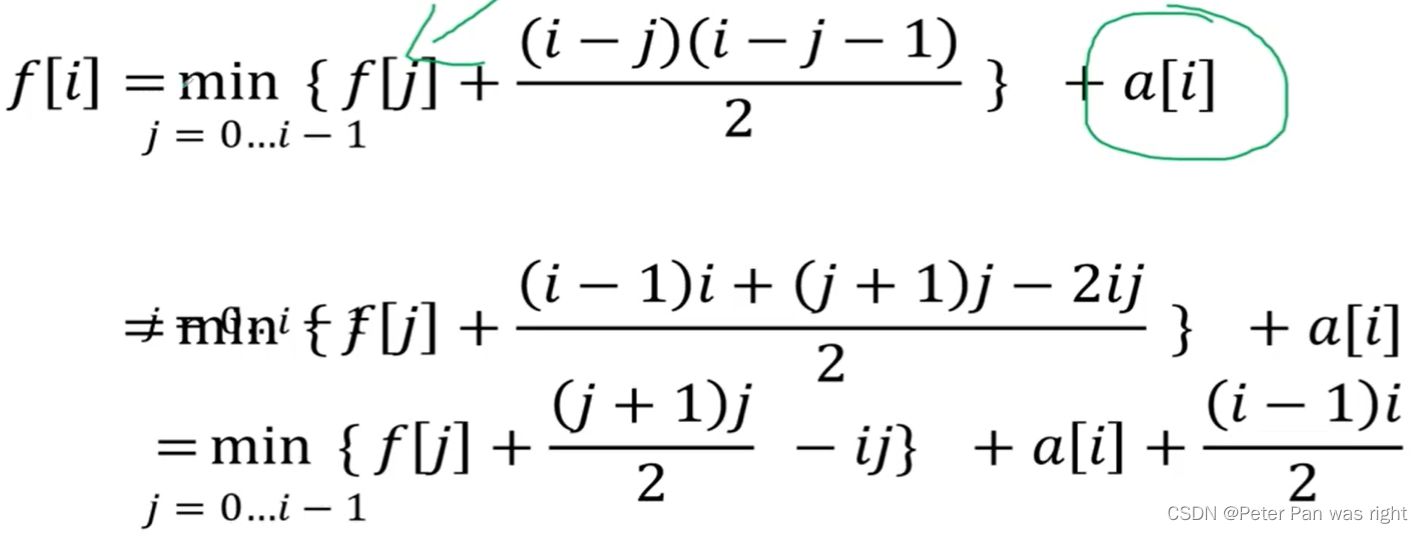斜率专题

计算数组的斜率，偏移，R2

模拟Excel中的R2的计算。 public bool fnCheckRear_R2(List<double[]> lRear, int iMinRear, int iMaxRear, ref double dR2) { bool bResult = true; int n = 0; dou

论斜率优化dp

论斜率优化dp 1问题2暴力算法-线性dp3斜率优化线性dp4后记 1问题如下图看到这题，题面很复杂其实可以转化为如下问题有 n n n个任务，排成一个有序序列，我们要解决这些任务总费用是每一个任务的完成时间乘以费用系数求和每个任务之前需要有一个机器启动时间 s s s 也就是说，一开始的时间为 0 0 0，做每个任务之前要先费 s s s的时间启动机器，做每个

斜率优化dp结论

斜率优化dp 一切的前提为：k<j<i，假设从j转移到i比从k转移到i更优(即靠后的j优)，去按照题目推导不等式，如果得到g(k,j)<f(i)，因为想在决策i的时候f(i)其实为常量,我们设为C=f(i)，则将前述不等式表述一般化：定理：对于下标k<j，如果g(k,j)<C，则靠后的j更优；否则，g(k,j)>C，靠前的k更优。结论：如果g(i,j)<C,最后求最优解时维护下凸包。证明：设由

【线性相关 vs 双变量回归】数据点在斜率周围的聚集程度与斜率本身并不是一回事。

相关性分析（具体来说，皮尔逊成对相关性）和回归分析（具体来说，双变量最小二乘 (OLS) 回归）具有许多共同的特征：两者都定期应用于两个连续变量（我们称之为 X 和 Y）。通常向学生介绍这两种图表时使用的是同一类型的图表：散点图。二者从根本上讲都是关于 X 中的偏差（即相对于平均值的单个值）与 Y 中的偏差之间的关系。两者都假设 X 和 Y 之间存在线性关系。两者都可以用于经典的假设检验，每个

[SCU 4516] Mingo's Game （斜率DP）

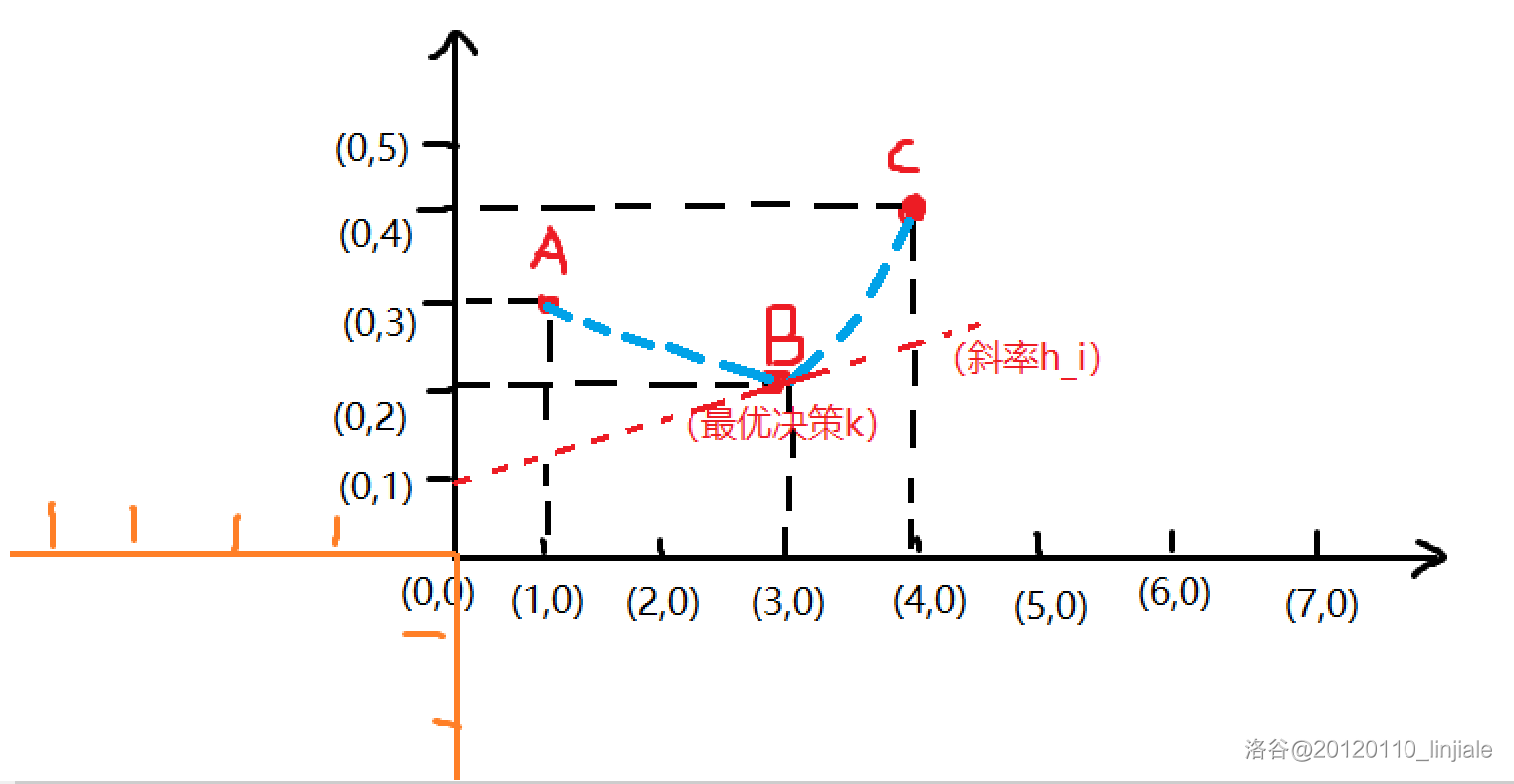
SCU - 4516 有 N个关卡，可以分为 K块，每个关卡都有个权值 ti t_i 每次选择最早没有通关的关卡块，设这个关卡包含了 [i,j] [i,j]的游戏选到最早没有通关的关卡是k, 选到 k的概率是 P=tk∑jx=ix P =\frac {t_k} {\sum_{x=i}^j x} 选到一个关卡一定能通关，花费一小时求合理分块的情况下，通关所有关卡块的期望时间最小

关于斜率大于1的中点画线的公式推导

首先还是假设直线L的一般公式为：Ax+By+C=0，并且斜率大于1，那么这个时候代表x变化慢，y变化快，那么这时我们应该让y每次递增1，x是否递增，需要判断，判断方法如下：首先假设直线的起点(x1,y1),终点为(x2,y2)，那么从起点开始，起点的下一个点的坐标应该是(x_next,y_next)，因为y每次递增1，所以y_next = y1+1,那么x_next应该取哪个点呢？设起点的

斜率优化详解

斜率优化 [HNOI2008] 玩具装箱状态转移方程： f i = m i n ( f i , f j + ( s u m i + i − s u m j − j − L ) 2 ) i > j f_i=min(f_i,f_j+(sum_i+i-sum_j-j-L)^2){i>j} fi=min(fi,fj+(sumi+i−sumj−j−L)2)i>j 设A为 s u m i

曲线斜率与法向量综合辨析

参考： http://wenku.baidu.com/link?url=AxjATkZdZg4NOER0_7dWz18OdacwtEWFcr5kZgmrBexxmJzS9M5D_fqlBsFIpBNlq1ZuZu6Qd6mg8fgXaayFA7O2IR4PXNseeYy9V_62bWW 用函数表达式与方程表达的变量之间关系是有一点点区别的。从一元看起。 y=f(x) y = f(x),

漫步微积分三——如何计算切线的斜率

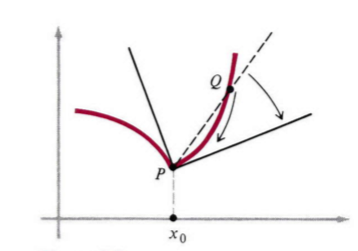
各种想法都有自己的一席之地，但是时间会剔除许多细节。 P＝(x0,y0) P＝(x_0,y_0)是抛物线 y＝x2 y＝x^2上的任意一个定点，如图1所示。作为基本思想的第一个图例，给定抛物线上一点 P P，计算切线的斜率。首先，我们选择曲线上的一个临近点Q=(x1,y1)Q=(x_1,y_1)。接下来，我们画出由这两点确定的割线 PQ PQ，割线的斜率明显是： msec=slope o

hdu-3669(斜率 dp)

题目链接这道题琢磨了好久，首先它要对 h进行降序排列对 w进行升序排列然后推出 dp 方程为 dp[i][j]=min(dp[k][j-1]+s[i].w*s[k+1].h) 推导斜率方程就是 k2 < k 使得 dp[k][j-1]+s[i].w*s[k+1].h < dp[k2][j-1]+s[i].w*s[k2+1].h; 移项得 dp[k][j-1]-dp[k2][j-1

BZOJ1010: [HNOI2008]玩具装箱toy（斜率优化dp）

Description 　　P教授要去看奥运，但是他舍不下他的玩具，于是他决定把所有的玩具运到北京。他使用自己的压缩器进行压缩，其可以将任意物品变成一堆，再放到一种特殊的一维容器中。P教授有编号为1…N的N件玩具，第i件玩具经过压缩后变成一维长度为Ci.为了方便整理，P教授要求在一个一维容器中的玩具编号是连续的。同时如果一个一维容器中有多个玩具，那么两件玩具之间要加入一个单位长度的填充物，形

Peter算法小课堂—动态规划斜率优化

大家来到这一堂课，就说明大家已经学过函数了直线方程：y=kx+b 大家可以算一算。其实，在数学上，这玩意要分类讨论那么，这唯一的交点就是我们要背出来的直线最值这像一个分段函数其实，只有部分直线能提供最小值，另外的，就可以省略当然，最大值也一样。看一下太戈编程第2627题题目在平面直角坐标系里，横坐标为x，纵坐标为y。有n条直线，第i

TLV277x和TLV277xA系列2.7V高斜率、轨到轨输出操作放大器

这份文件是关于TLV277x和TLV277xA系列2.7V高斜率率、轨到轨输出操作放大器的数据手册，由德州仪器（Texas Instruments）发布。这些放大器具有关闭模式，适用于便携式应用和汽车高可靠性应用。以下是文件的核心内容概要：产品特性：产品特性详细描述如下： 1. **高斜率率 (Slew Rate)**:- 10.5 V/µs 典型值，表示放大器输出电压变化的速率，这对于

HDU 2829 [Lawrence] DP斜率优化

解题思路首先肯定是考虑如何快速求出一段铁路的价值。\[ \sum_{i=1}^k \sum_{j=1, j\neq i}^kA[i]A[j]=(\sum_{i=1}^kA[i])^2-\sum_{i=1}^kA[i]^2 \] 那么我们要维护如下两个东西，就可以在$O(1)$内求出一段铁路的价值了。 for( LL i = 1; i <= N; ++i ) Sum[ i ] = Sum[

HDU 3669 [Cross the Wall] DP斜率优化

问题分析首先，如果一个人的$w$和$h$均小于另一个人，那么这个人显然可以被省略。如果我们将剩下的人按$w[i]$递增排序，那么$h[i]$就是递减。之后我们考虑DP。我们设$f[i][j]$为到第$i$个人，打了$j$个洞的花费。于是我们可以得到如下DP过程： for( LL i = 1; i <= N; ++i ) F[ i ][ 1 ] = w[ i ]

HDU 3480 Division DP斜率优化

解题思路第一步显然是将原数组排序嘛……然后分成一些不相交的子集，这样显然最小。重点是怎么分。首先，我们写出一个最暴力的$DP$：我们令$F[ i ][ j ] $ 为到第$i$位，分成$j$组的代价，我们可以写出如下 $ DP$ for( LL i = 1; i <= N; ++i ) F[ i ][ 1 ] = sqr( A[ i ] - A[ 1 ] );for( LL

HDU 3507 [Print Article]DP斜率优化

题目大意给定一个长度为$n(n \leqslant 500000)$的数列，将其分割为连续的若干份，使得 $ \sum ((\sum_{i=j}^kC_i) +M) $ 最小。其中$C_i$为序列中的项的值，$M$为常数。$ j,k $ 表示在原序列中连续的某一段的起始位置和结束位置。解题思路考虑到$n$的范围巨大，肯定不能用$O(n^2)$的暴力DP，而贪心又显然有问

BZOJ 1096 [ZJOI2007]仓库建设动态规划+斜率优化

Description 　　L公司有N个工厂，由高到底分布在一座山上。如图所示，工厂1在山顶，工厂N在山脚。由于这座山处于高原内陆地区（干燥少雨），L公司一般把产品直接堆放在露天，以节省费用。突然有一天，L公司的总裁L先生接到气象部门的电话，被告知三天之后将有一场暴雨，于是L先生决定紧急在某些工厂建立一些仓库以免产品被淋坏。由于地形的不同，在不同工厂建立仓库的费用可能是不同的。第i个工厂

bzoj4700 适者 CDQ分治+斜率优化毒瘤题

题目链接：传送门对于每个敌方的人形兵器，记录一个 B B B，表示多少次能够打死这个人形兵器。易知 B i = ⌈ D i A T K ⌉ B_i=\lceil\frac{D_i}{ATK}\rceil Bi=⌈ATKDi⌉。首先考虑没有秒杀的情况：显然应该按照某个顺序打死所有人形兵器（不可能打人形兵器A打到一半突然开始打B），所以考虑什么时候交换人形兵器 i , i + 1 i,

LOJ #2483 [CEOI2017]Building Bridges CDQ分治+斜率优化

题目链接：传送门洛咕传送门令 s u m w sumw sumw表示 w w w的前缀和。显然的 d p dp dp方程： d p [ i ] = m i n ( d p [ j ] + ( h [ i ] − h [ j ] ) 2 + s u m w [ i − 1 ] − s u m w [ j ] ) dp[i]=min(dp[j]+(h[i]-h[j])^2+sumw[i-1]-

bzoj2726 洛谷P2365 [SDOI2012]任务安排 cdq分治+斜率优化

题目链接： bzoj2726 洛谷2365 洛咕上好像 O ( n 2 ) O(n^2) O(n2)能过……还没有负数的情况…… 如果没有负数，就直接大莉上斜率优化就珂以了qwq 转移方程是 d p [ i ] = d p [ j ] + s u m T [ i ] ∗ ( c [ i ] − c [ j ] ) + S ∗ ( c [ n ] − c [ j ] ) dp[i]=dp[j]+s

斜率优化dp 笔记

任务安排1 有 N 个任务排成一个序列在一台机器上等待执行，它们的顺序不得改变。机器会把这 N 个任务分成若干批，每一批包含连续的若干个任务。从时刻 00 开始，任务被分批加工，执行第 i 个任务所需的时间是 Ti。另外，在每批任务开始前，机器需要 S 的启动时间，故执行一批任务所需的时间是启动时间 S 加上每个任务所需时间之和。一个任务执行后，将在机器中稍作等待，直至该批任务全

力扣面试150 直线上最多的点数数学直线斜率欧几里得求最大公约数

Problem: 149. 直线上最多的点数思路 👨‍🏫 参考题解 💖 枚举直线 + 枚举统计时间复杂度: O ( n 3 ) O(n^3) O(n3) 空间复杂度: O ( 1 ) O(1) O(1) class Solution {public int maxPoints(int[][] points){int n = points.length;int

判断一组数据的变化趋势：斜率法和cox_stuart趋势检验

斜率法 '''1.做最小二乘拟合，把序列拟合成一条直线;2.根据直线的斜率k可以得知序列的主要走势：例如：(1)k > 0.1763 上升 (2) k < -0.1763 下降 (3)其他3.然后计算序列各点到直线的距离（和方差一样）设定一个阈值L，统计超过L的点数目，点数目越多说明序列震荡越厉害'''import numpy as npimport mathdef t

[JSOI2011] 柠檬（斜率优化DP，优化技巧）

题面描述题面简要题意：给出一个长度为 n n n 的整数序列 s i s_i si。可以将序列任意划分成若干非空连续段。对于每一段，可以选择一个整数 s 0 s_0 s0，若该段 s 0 s_0 s0 的数量为 t t t，则该段的价值为 s 0 × t 2 s_0 \times t^2 s0×t2。请求出每一段价值之和的最大值。 1

【bzoj1096】【ZJOI2007】【仓库建设】【斜率优化dp】

Description L公司有N个工厂，由高到底分布在一座山上。如图所示，工厂1在山顶，工厂N在山脚。由于这座山处于高原内陆地区（干燥少雨），L公司一般把产品直接堆放在露天，以节省费用。突然有一天，L公司的总裁L先生接到气象部门的电话，被告知三天之后将有一场暴雨，于是L先生决定紧急在某些工厂建立一些仓库以免产品被淋坏。由于地形的不同，在不同工厂建立仓库的费用可能是不同的。第i个工厂目前已有成