本文主要是介绍Peter算法小课堂—动态规划斜率优化,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
大家来到这一堂课,就说明大家已经学过函数了
直线方程:y=kx+b

大家可以算一算。
其实,在数学上,这玩意要分类讨论

那么,这唯一的交点就是我们要背出来的
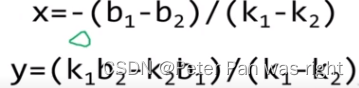
直线最值

这像一个分段函数

其实,只有部分直线能提供最小值,另外的,就可以省略
当然,最大值也一样。
看一下太戈编程第2627题
题目
在平面直角坐标系里,横坐标为x,纵坐标为y。有n条直线,第i条直线的形式为:y=b[i]+k[i]*x。其中整数b[i]为截距,整数k[i]为斜率。已知k[i]随着i的增加而减小。另外有m个从小到大排布的横坐标,第i个为x[i]。请求出在每个横坐标位置上各个直线的纵坐标最小值是多少?(纯数学)
暴力
struct Line{ll b,k;} lines[N];
int main(){ll n,m;cin>>n>>m;for(ll i=1;i<=n;i++) cin>>lines[i].b;for(ll i=1;i<=n;i++) cin>>lines[i].k;for(ll i=1;i<=m;i++) cin>>x[i];for(ll i=1;i<=m;i++){ans[i]=INF;for(ll j=1;j<=n;j++){ans[i]=min(ans[i],lines[j].b+lines[j].k*x[i]);}}for(int i=1;i<=m;i++) cout<<ans[i]<<" ";return 0;
}时间复杂度不太行
优化
根据前面的分析,

但是,这好像只能做到常数级别的优化

注意:斜率递减
2号和0号的节点在2号和1号节点左侧,那么说明,1号线是废线,可以省略。
做之前,要做准备工作
struct Line{ll b,k;} lines[N];
ld X(ll u,ll v){return -(ld)(lines[u].b-lines[v].b)/(lines[u].k-lines[v].k);
}然后,我们维护一个队列,里面是可能参与最小值的直线编号
ll l=1,r=1;
for(ll i=1;i<=n;++i){while(r-l>=2&&X(i,q[r-1])<X(q[r-1],q[r-2])) r--;q[r++]=i;
}筛完了,剩下一个上凸轮廓。那么,一条直线只会提供一部分最小,之后的我们称之为“过气的直线”
假设现在有两条直线l,l+1,程序运行到x[i]。当x[i]在交点右侧时,l+1提供最小;当x[i]在交点左侧时,l+1不能提供最小。
for(ll i=1;i<=m;++i){while(r-l>=2&&X(q[l],q[l+1])<x[i]) ++l;int j=q[l];ans[i]=lines[j].b+lines[j].k*x[i];
}书籍叠放1
题目
你有n本书,编号1到n,需要分几堆叠放在桌面上。每本书的正面都是一个长方形,共四条边,左右两侧边长对应长方形的长度,上下两侧边长对应长方形的宽度。第i本书的长度为h[i],宽度为w[i]。你可以选择任意几本书分出任意的堆数。但是,叠放的时候要注意,每本书两两之间都保持上下左右四条边平行,不能旋转。每组叠放好的书都会在桌面上占据一定的面积。例如我们将3本书叠放在一堆里:第一本长度为1宽度为4,第二本长度为2宽度为3,第三本长度为3宽度为2,这三本占据的面积为长度为3宽度为4的长方形面积,也就是3*4=12。
目前,已知你的书籍满足一种特殊顺序:你发现随着编号i增加,书的长度h[i]增加,宽度w[i]减少。请问,经过合理叠放后,总体占据的面积最小是多少?
这是一道dp题,可以用朴素
朴素
cin>>n;
for(ll i=1;i<=n;i++) cin>>bk[i].h>bk[i].w;
for(ll i=1;i<=n;++i){f[i]=bk[1].w*bk[i]*h;for(ll j=1;j<i;++j)f[i]=min(f[i],f[j]+bk[j+1].w*bk[i].h);
}优化

这个看起来像直线最值吗

解释完毕
索道选址II
题目描述
lester的老家有一个著名的旅游景点:大牛山。据说爬完就能成为C++大牛,所以游客不断。从山脚到山顶共有n个景点,排成一条直线。山顶为景点n,并且只有这一条登山路线orz。由于山太高,当地政府决定架设若干条索道站点。索道站点山上某个景点,并且到山顶(景点n)是必须有索道站点的。在景点i修建索道站点的花费为Ai。对于没有索道直达的景点,游客会乘坐高于该景点且最近的一个索道站点,然后从该站点向下走到目的地。步行游客会产生一定的不满意度,值等于索道站点与目的地编号之差。你可以认为想去每个景点的游客人数是相同的,例如索道站点在景点3,6,则去景点4需要先到景点6,然后向下走到景点4,不满意度为6-4=2。lester既不想花太多钱,又不愿意积累太多的不满意度。注意:游客出发的位置可以理解为在0号,而不是1号。他希望求一种折衷方案,使得花费与不满意度总和最小。
f[i]表示用前i个选址覆盖前i个景点最小代价,且上一段为j。则不满意度为
也就是j+1加到i-1。
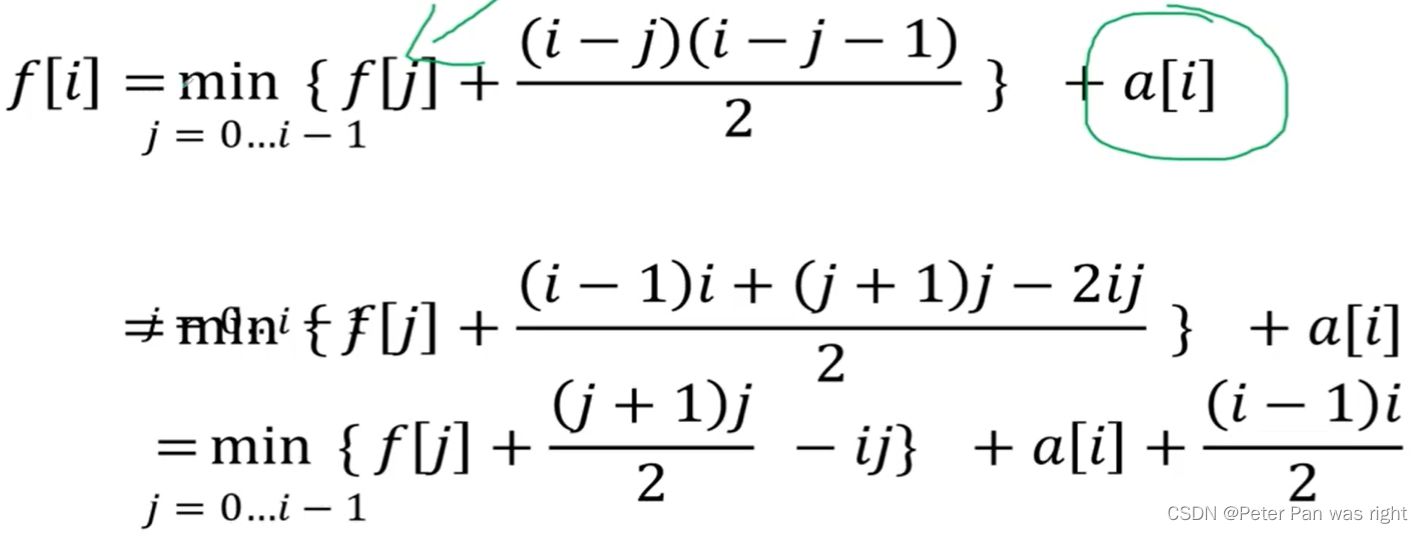
最后,我们以-j为斜率,f[j]+1/2*(j+1)*j为截距画直线
这篇关于Peter算法小课堂—动态规划斜率优化的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








