规划专题
动态规划---打家劫舍
题目: 你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。 给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。 思路: 动态规划五部曲: 1.确定dp数组及含义 dp数组是一维数组,dp[i]代表
软考系统规划与管理师考试证书含金量高吗?
2024年软考系统规划与管理师考试报名时间节点: 报名时间:2024年上半年软考将于3月中旬陆续开始报名 考试时间:上半年5月25日到28日,下半年11月9日到12日 分数线:所有科目成绩均须达到45分以上(包括45分)方可通过考试 成绩查询:可在“中国计算机技术职业资格网”上查询软考成绩 出成绩时间:预计在11月左右 证书领取时间:一般在考试成绩公布后3~4个月,各地领取时间有所不同
poj 2976 分数规划二分贪心(部分对总体的贡献度) poj 3111
poj 2976: 题意: 在n场考试中,每场考试共有b题,答对的题目有a题。 允许去掉k场考试,求能达到的最高正确率是多少。 解析: 假设已知准确率为x,则每场考试对于准确率的贡献值为: a - b * x,将贡献值大的排序排在前面舍弃掉后k个。 然后二分x就行了。 代码: #include <iostream>#include <cstdio>#incl
代码随想录冲冲冲 Day39 动态规划Part7
198. 打家劫舍 dp数组的意义是在第i位的时候偷的最大钱数是多少 如果nums的size为0 总价值当然就是0 如果nums的size为1 总价值是nums[0] 遍历顺序就是从小到大遍历 之后是递推公式 对于dp[i]的最大价值来说有两种可能 1.偷第i个 那么最大价值就是dp[i-2]+nums[i] 2.不偷第i个 那么价值就是dp[i-1] 之后取这两个的最大值就是d
数学建模笔记—— 非线性规划
数学建模笔记—— 非线性规划 非线性规划1. 模型原理1.1 非线性规划的标准型1.2 非线性规划求解的Matlab函数 2. 典型例题3. matlab代码求解3.1 例1 一个简单示例3.2 例2 选址问题1. 第一问 线性规划2. 第二问 非线性规划 非线性规划 非线性规划是一种求解目标函数或约束条件中有一个或几个非线性函数的最优化问题的方法。运筹学的一个重要分支。2
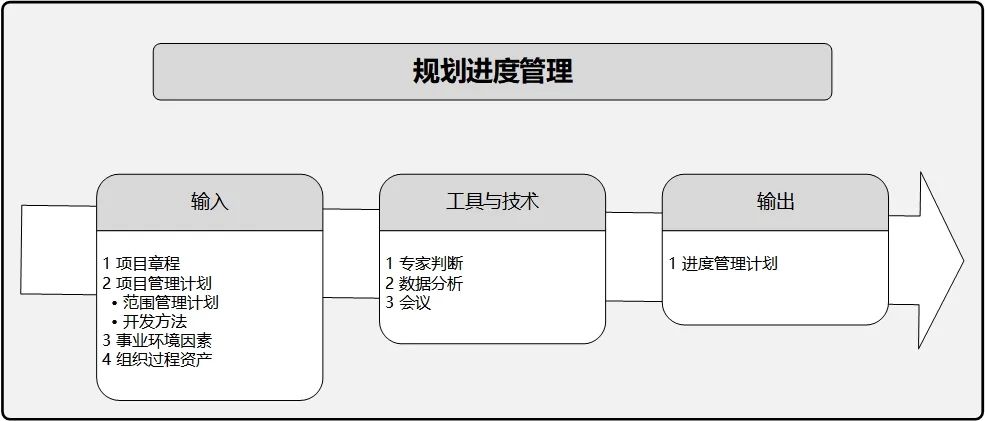
PMBOK® 第六版 规划进度管理
目录 读后感—PMBOK第六版 目录 规划进度管理主要关注为整个项目期间的进度管理提供指南和方向。以下是两个案例,展示了进度管理中的复杂性和潜在的冲突: 案例一:近期,一个长期合作的客户因政策要求,急需我们为多家医院升级一个小功能。在这个过程中出现了三个主要问题: 在双方确认接口协议后,客户私自修改接口并未通知我们,直到催进度时才发现这个问题关于UI设计的部分,后台开发人员未将其传递给
LeetCode:64. 最大正方形 动态规划 时间复杂度O(nm)
64. 最大正方形 题目链接 题目描述 给定一个由 0 和 1 组成的二维矩阵,找出只包含 1 的最大正方形,并返回其面积。 示例1: 输入: 1 0 1 0 01 0 1 1 11 1 1 1 11 0 0 1 0输出: 4 示例2: 输入: 0 1 1 0 01 1 1 1 11 1 1 1 11 1 1 1 1输出: 9 解题思路 这道题的思路是使用动态规划
LeetCode:3177. 求出最长好子序列 II 哈希表+动态规划实现n*k时间复杂度
3177. 求出最长好子序列 II 题目链接 题目描述 给你一个整数数组 nums 和一个非负整数k 。如果一个整数序列 seq 满足在下标范围 [0, seq.length - 2] 中 最多只有 k 个下标i满足 seq[i] != seq[i + 1] ,那么我们称这个整数序列为好序列。请你返回 nums中好子序列的最长长度。 实例1: 输入:nums = [1,2,1,1,3],
实现的动态规划问题华为笔试题C++实现
秋招刷力扣题,我觉得我对动态规划不是熟练,在此处做总结 动态规划(Dynamic Programming,DP)算法通常用于求解某种具有最优性质的问题。在这类问题中,可能会有许多可行解,每一个解都对应一个值,我们希望找到具有最优值的解。我觉得最大的问题就是对问题的分解,分解后的问题与分解前的问题具有相同的决策机制,将决策机制进行抽象,最终可以得到对应的解; 动态规划中开始介绍的爬楼梯等问题,答
BUYING FEED(贪心+树状动态规划)
BUYING FEED 时间限制: 3000 ms | 内存限制: 65535 KB 难度:4 描述 Farmer John needs to travel to town to pick up K (1 <= K <= 100)pounds of feed. Driving D miles with K pounds of feed in his truck costs D
【UVA】1626-Brackets sequence(动态规划)
一道算是比较难理解的动规。 状态转移分2个: (用d[i][j]表示在i~j内最少需要添加几个括号,保持平衡) 1.如果s[i]和s[j]是一对括号,那么d[i][j] = d[i + 1][j - 1] 2.否则的话 d[i][j] = min(d[i][k],[k + 1][j]); 边界是d[i + 1][i] = 0; d[i][i] = 1; 13993644 162
【UVA】11584-Partitioning by Palindromes(动态规划)
动态规划。 如果 j + 1 ~ i是回文,那么 dp[i] = min=(dp[j] + 1); 判断j + 1~ i是不是回文可以进行预处理,方法是枚举中心,之后向两边伸张,(需要枚举2次,一次是偶数回文,一次是奇数回文) 13993253 11584 Partitioning by Palindromes Accepted C++ 0.132 2014-08-05 08:2
【UVA】11400-Lighting System Design(动态规划)
这道题感觉状态式不是很好推。。。 WA了好几次是因为排序的时候出问题了。 这道题出在线性结构里了,先说一下最长上升子序列吧。 dp[i]代表了以array[i]结尾的时候,最长子序列长度。 推导的时候,以起点递增的顺序进行推导。 #include<cstdio>#include<cstring>#include<iostream>#include<algorithm>#i
【uva】116-Unidirectional TSP(动态规划,路径问题)
一道很基础的动态规划,不过需要考虑路径(而且是最小字典序)。 转移方程很好写: d[i][j] = min(dp[i + 1][ j] ,dp[i + 1][j - 1] ,dp[i + 1][ j - 1]) + mat[j[i]; dp[i][j]代表走到第i列第行的时候距离最后一行的最短距离; 13991881 116 Unidirectional TSP Accepted C
437 - The Tower of Babylon(动态规划)
这题感觉比较水了,只不过建立模型的时候需要想一下,给n个长方体,我们不妨给它长宽高固定的3个长方体。 之后根据长宽的大小排序。 dp[i]代表第i个长方体当顶面的时候的高度,所以初始的时候dp[i] = cub[i[.h, dp[i] = dp[j] + cub[i[.h(当j的长宽均严格小于i的时候成立) 13989891 437 The Tower of Babylon Acce
【UVA】10003-Cutting Sticks(动态规划、矩阵链乘)
一道动态规划题,不过似乎可以用回溯水过去,回溯的话效率很烂的。 13988658 10003 Cutting Sticks Accepted C++ 1.882 2014-08-04 09:26:49 AC代码: #include<cstdio>#include<cstring>#include<iostream>#include<algorithm>#include
国际象棋问题(动态规划)
问题描述:国际象棋中的车可以水平的或竖直的移动,一个车要从一个棋盘的左上角(0,0)移到(n,m)这个坐标,有多少种最短路径? 设走到(i,j)的方法为dp(i,j),那么根据递推可以得到dp(i,j) = dp(i,j - 1) + dp(i - 1, j),边界条件下,dp(i,0) = 1, dp(0,j) = 1; #include<cstdio>#include<cstring
【UVA】10739 - String to Palindrome(动态规划)
比较水的动态规划 dp[i][j] 将原串 i ~ j 之内的字符转化为回文字符所需要的最小操作次数 其中删除操作和添加操作本质上是一样的。 三个状态转移方程: dp[i][j] = min(dp[i][j] ,dp[i + 1][j]); dp[i][j] = min(dp[i][j] ,dp[i + 1][j - 1]); dp[i][j] = min(dp[i][j] ,dp[
第二天旅游线路规划和预览
第二天:从克拉玛依市乌尔禾区到五彩滩,晚上住宿贾登峪; 规划结果见下图: 1、行程安排 根据上面的耗时情况,规划一天的行程安排如下: 1)早上7:30起床,吃完早饭,8:30出发; 2)从克拉玛依市乌尔禾区到五彩滩风景区,路程229公里,车程3小时,中午12:00左右到达五彩滩景区; 3)中午吃饭1小时; 3)五彩滩游玩时间约3小时,在五彩滩游玩到16:00; 4)乘车前往阿勒泰地区布尔津县
动态规划---单词拆分
题目: 给你一个字符串 s 和一个字符串列表 wordDict 作为字典。如果可以利用字典中出现的一个或多个单词拼接出 s 则返回 true。 注意:不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。 思路:本题属于完全背包问题,字符串s的长度为背包容量,字符串列表wordDict中的每一个元素相当于物品。 动态规划五部曲: 1.确定dp数组及含义 dp数组为元素类型是布
MATLAB中的矩阵在目标规划中的应用_以linprog为例
目标规划是一种数学规划方法,它允许在多个目标之间进行权衡,以找到最优解。 在MATLAB中,可以使用优化工具箱中的函数来求解目标规划问题。例如,`linprog` 函数可以用于求解线性规划问题,而 `fmincon` 函数可以用于求解有约束的非线性规划问题。对于多目标规划,可以使用 `fgoalattain` 函数来求解,该函数允许设置目标函数希望达到的目标值和权重。 在数学方程模型建立完成之
力扣 | 递归 | 区间上的动态规划 | 486. 预测赢家
文章目录 一、递归二、区间动态规划 LeetCode:486. 预测赢家 一、递归 注意到本题数据范围为 1 < = n < = 20 1<=n<=20 1<=n<=20,因此可以使用递归枚举选择方式,时间复杂度为 2 20 = 1024 ∗ 1024 = 1048576 = 1.05 × 1 0 6 2^{20} = 1024*1024=1048576=1.05 × 10^
中小型局域网组网规划与实施
一、绪论 1.1 背景 本课题以中小型企业网络搭建为背景,实现网络规划与设计和模拟。该企业网有四个部门,人力部、研发部、市场部和财务部,不同部门分别划分VLAN,不同VLAN之间分配不同的IP地址段。内外网之间要互通。 1.2 发展趋势 市场经济的快速发展和计算机网络的普及使得网络与人们的日常生活越来越密切。在我们日常生活中,网络随处可见,常见的就有移动网络,有线网络,无线网络,视
算法图解(8~10贪心,动态规划,K最近邻算法)
贪心算法 在每一步都选择局部最优解,从而期望最终得到全局最优解。 贪心算法并不总能保证全局最优解,因此需要满足以下两个条件: 贪心选择性质:可以通过局部最优选择构造出全局最优解。最优子结构:问题的最优解包含其子问题的最优解。 实例:给定面额的硬币,用最少硬币凑出指定金额 int minCoins(vector<int>& coins, int amount) {int count = 0
leetcode:3176 求出最长好子序列 使用动态规划
3176. 求出最长好子序列 题目链接https://leetcode.cn/problems/find-the-maximum-length-of-a-good-subsequence-i/ 题目描述 给你一个整数数组 nums 和一个非负整数k 。如果一个整数序列 seq 满足在下标范围 [0, seq.length - 2] 中 最多只有 k 个下标 i 满足 seq[i] != se