动态专题
MySQL中动态生成SQL语句去掉所有字段的空格的操作方法
《MySQL中动态生成SQL语句去掉所有字段的空格的操作方法》在数据库管理过程中,我们常常会遇到需要对表中字段进行清洗和整理的情况,本文将详细介绍如何在MySQL中动态生成SQL语句来去掉所有字段的空... 目录在mysql中动态生成SQL语句去掉所有字段的空格准备工作原理分析动态生成SQL语句在MySQL
Java调用C++动态库超详细步骤讲解(附源码)
《Java调用C++动态库超详细步骤讲解(附源码)》C语言因其高效和接近硬件的特性,时常会被用在性能要求较高或者需要直接操作硬件的场合,:本文主要介绍Java调用C++动态库的相关资料,文中通过代... 目录一、直接调用C++库第一步:动态库生成(vs2017+qt5.12.10)第二步:Java调用C++
C#如何动态创建Label,及动态label事件
《C#如何动态创建Label,及动态label事件》:本文主要介绍C#如何动态创建Label,及动态label事件,具有很好的参考价值,希望对大家有所帮助,如有错误或未考虑完全的地方,望不吝赐教... 目录C#如何动态创建Label,及动态label事件第一点:switch中的生成我们的label事件接着,
SpringCloud动态配置注解@RefreshScope与@Component的深度解析
《SpringCloud动态配置注解@RefreshScope与@Component的深度解析》在现代微服务架构中,动态配置管理是一个关键需求,本文将为大家介绍SpringCloud中相关的注解@Re... 目录引言1. @RefreshScope 的作用与原理1.1 什么是 @RefreshScope1.
MyBatis 动态 SQL 优化之标签的实战与技巧(常见用法)
《MyBatis动态SQL优化之标签的实战与技巧(常见用法)》本文通过详细的示例和实际应用场景,介绍了如何有效利用这些标签来优化MyBatis配置,提升开发效率,确保SQL的高效执行和安全性,感... 目录动态SQL详解一、动态SQL的核心概念1.1 什么是动态SQL?1.2 动态SQL的优点1.3 动态S
mybatis-plus 实现查询表名动态修改的示例代码
《mybatis-plus实现查询表名动态修改的示例代码》通过MyBatis-Plus实现表名的动态替换,根据配置或入参选择不同的表,本文主要介绍了mybatis-plus实现查询表名动态修改的示... 目录实现数据库初始化依赖包配置读取类设置 myBATis-plus 插件测试通过 mybatis-plu
基于Canvas的Html5多时区动态时钟实战代码
《基于Canvas的Html5多时区动态时钟实战代码》:本文主要介绍了如何使用Canvas在HTML5上实现一个多时区动态时钟的web展示,通过Canvas的API,可以绘制出6个不同城市的时钟,并且这些时钟可以动态转动,每个时钟上都会标注出对应的24小时制时间,详细内容请阅读本文,希望能对你有所帮助...
Vue中动态权限到按钮的完整实现方案详解
《Vue中动态权限到按钮的完整实现方案详解》这篇文章主要为大家详细介绍了Vue如何在现有方案的基础上加入对路由的增、删、改、查权限控制,感兴趣的小伙伴可以跟随小编一起学习一下... 目录一、数据库设计扩展1.1 修改路由表(routes)1.2 修改角色与路由权限表(role_routes)二、后端接口设计
前端 CSS 动态设置样式::class、:style 等技巧(推荐)
《前端CSS动态设置样式::class、:style等技巧(推荐)》:本文主要介绍了Vue.js中动态绑定类名和内联样式的两种方法:对象语法和数组语法,通过对象语法,可以根据条件动态切换类名或样式;通过数组语法,可以同时绑定多个类名或样式,此外,还可以结合计算属性来生成复杂的类名或样式对象,详细内容请阅读本文,希望能对你有所帮助...
Nginx实现动态封禁IP的步骤指南
《Nginx实现动态封禁IP的步骤指南》在日常的生产环境中,网站可能会遭遇恶意请求、DDoS攻击或其他有害的访问行为,为了应对这些情况,动态封禁IP是一项十分重要的安全策略,本篇博客将介绍如何通过NG... 目录1、简述2、实现方式3、使用 fail2ban 动态封禁3.1 安装 fail2ban3.2 配
Vue3中的动态组件详解
《Vue3中的动态组件详解》本文介绍了Vue3中的动态组件,通过`component:is=动态组件名或组件对象/component`来实现根据条件动态渲染不同的组件,此外,还提到了使用`markRa... 目录vue3动态组件动态组件的基本使用第一种写法第二种写法性能优化解决方法总结Vue3动态组件动态
Android 悬浮窗开发示例((动态权限请求 | 前台服务和通知 | 悬浮窗创建 )
《Android悬浮窗开发示例((动态权限请求|前台服务和通知|悬浮窗创建)》本文介绍了Android悬浮窗的实现效果,包括动态权限请求、前台服务和通知的使用,悬浮窗权限需要动态申请并引导... 目录一、悬浮窗 动态权限请求1、动态请求权限2、悬浮窗权限说明3、检查动态权限4、申请动态权限5、权限设置完毕后
Java使用POI-TL和JFreeChart动态生成Word报告
《Java使用POI-TL和JFreeChart动态生成Word报告》本文介绍了使用POI-TL和JFreeChart生成包含动态数据和图表的Word报告的方法,并分享了实际开发中的踩坑经验,通过代码... 目录前言一、需求背景二、方案分析三、 POI-TL + JFreeChart 实现3.1 Maven
Java导出Excel动态表头的示例详解
《Java导出Excel动态表头的示例详解》这篇文章主要为大家详细介绍了Java导出Excel动态表头的相关知识,文中的示例代码简洁易懂,具有一定的借鉴价值,有需要的小伙伴可以了解下... 目录前言一、效果展示二、代码实现1.固定头实体类2.动态头实现3.导出动态头前言本文只记录大致思路以及做法,代码不进
vue基于ElementUI动态设置表格高度的3种方法
《vue基于ElementUI动态设置表格高度的3种方法》ElementUI+vue动态设置表格高度的几种方法,抛砖引玉,还有其它方法动态设置表格高度,大家可以开动脑筋... 方法一、css + js的形式这个方法需要在表格外层设置一个div,原理是将表格的高度设置成外层div的高度,所以外层的div需要
SpringBoot实现动态插拔的AOP的完整案例
《SpringBoot实现动态插拔的AOP的完整案例》在现代软件开发中,面向切面编程(AOP)是一种非常重要的技术,能够有效实现日志记录、安全控制、性能监控等横切关注点的分离,在传统的AOP实现中,切... 目录引言一、AOP 概述1.1 什么是 AOP1.2 AOP 的典型应用场景1.3 为什么需要动态插
VUE动态绑定class类的三种常用方式及适用场景详解
《VUE动态绑定class类的三种常用方式及适用场景详解》文章介绍了在实际开发中动态绑定class的三种常见情况及其解决方案,包括根据不同的返回值渲染不同的class样式、给模块添加基础样式以及根据设... 目录前言1.动态选择class样式(对象添加:情景一)2.动态添加一个class样式(字符串添加:情
SpringCloud配置动态更新原理解析
《SpringCloud配置动态更新原理解析》在微服务架构的浩瀚星海中,服务配置的动态更新如同魔法一般,能够让应用在不重启的情况下,实时响应配置的变更,SpringCloud作为微服务架构中的佼佼者,... 目录一、SpringBoot、Cloud配置的读取二、SpringCloud配置动态刷新三、更新@R
如何用Python绘制简易动态圣诞树
《如何用Python绘制简易动态圣诞树》这篇文章主要给大家介绍了关于如何用Python绘制简易动态圣诞树,文中讲解了如何通过编写代码来实现特定的效果,包括代码的编写技巧和效果的展示,需要的朋友可以参考... 目录代码:效果:总结 代码:import randomimport timefrom math
Java中JSON字符串反序列化(动态泛型)
《Java中JSON字符串反序列化(动态泛型)》文章讨论了在定时任务中使用反射调用目标对象时处理动态参数的问题,通过将方法参数存储为JSON字符串并进行反序列化,可以实现动态调用,然而,这种方式容易导... 需求:定时任务扫描,反射调用目标对象,但是,方法的传参不是固定的。方案一:将方法参数存成jsON字
.NET利用C#字节流动态操作Excel文件
《.NET利用C#字节流动态操作Excel文件》在.NET开发中,通过字节流动态操作Excel文件提供了一种高效且灵活的方式处理数据,本文将演示如何在.NET平台使用C#通过字节流创建,读取,编辑及保... 目录用C#创建并保存Excel工作簿为字节流用C#通过字节流直接读取Excel文件数据用C#通过字节
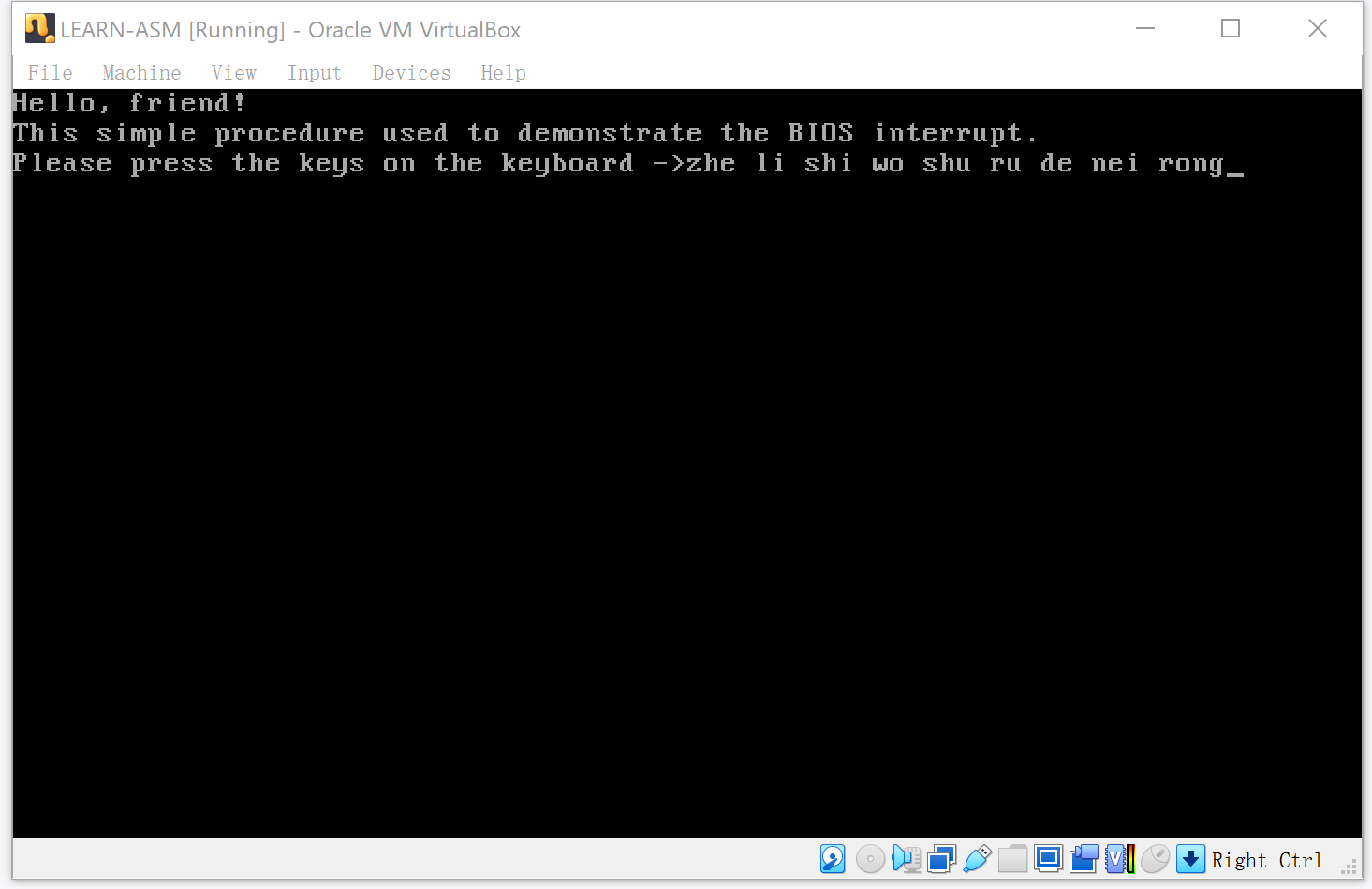
第10章 中断和动态时钟显示
第10章 中断和动态时钟显示 从本章开始,按照书籍的划分,第10章开始就进入保护模式(Protected Mode)部分了,感觉从这里开始难度突然就增加了。 书中介绍了为什么有中断(Interrupt)的设计,中断的几种方式:外部硬件中断、内部中断和软中断。通过中断做了一个会走的时钟和屏幕上输入字符的程序。 我自己理解中断的一些作用: 为了更好的利用处理器的性能。协同快速和慢速设备一起工作
动态规划---打家劫舍
题目: 你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。 给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。 思路: 动态规划五部曲: 1.确定dp数组及含义 dp数组是一维数组,dp[i]代表
代码随想录冲冲冲 Day39 动态规划Part7
198. 打家劫舍 dp数组的意义是在第i位的时候偷的最大钱数是多少 如果nums的size为0 总价值当然就是0 如果nums的size为1 总价值是nums[0] 遍历顺序就是从小到大遍历 之后是递推公式 对于dp[i]的最大价值来说有两种可能 1.偷第i个 那么最大价值就是dp[i-2]+nums[i] 2.不偷第i个 那么价值就是dp[i-1] 之后取这两个的最大值就是d
LeetCode:64. 最大正方形 动态规划 时间复杂度O(nm)
64. 最大正方形 题目链接 题目描述 给定一个由 0 和 1 组成的二维矩阵,找出只包含 1 的最大正方形,并返回其面积。 示例1: 输入: 1 0 1 0 01 0 1 1 11 1 1 1 11 0 0 1 0输出: 4 示例2: 输入: 0 1 1 0 01 1 1 1 11 1 1 1 11 1 1 1 1输出: 9 解题思路 这道题的思路是使用动态规划
vue2实践:el-table实现由用户自己控制行数的动态表格
需求 项目中需要提供一个动态表单,如图: 当我点击添加时,便添加一行;点击右边的删除时,便删除这一行。 至少要有一行数据,但是没有上限。 思路 这种每一行的数据固定,但是不定行数的,很容易想到使用el-table来实现,它可以循环读取:data所绑定的数组,来生成行数据,不同的是: 1、table里面的每一个cell,需要放置一个input来支持用户编辑。 2、最后一列放置两个b