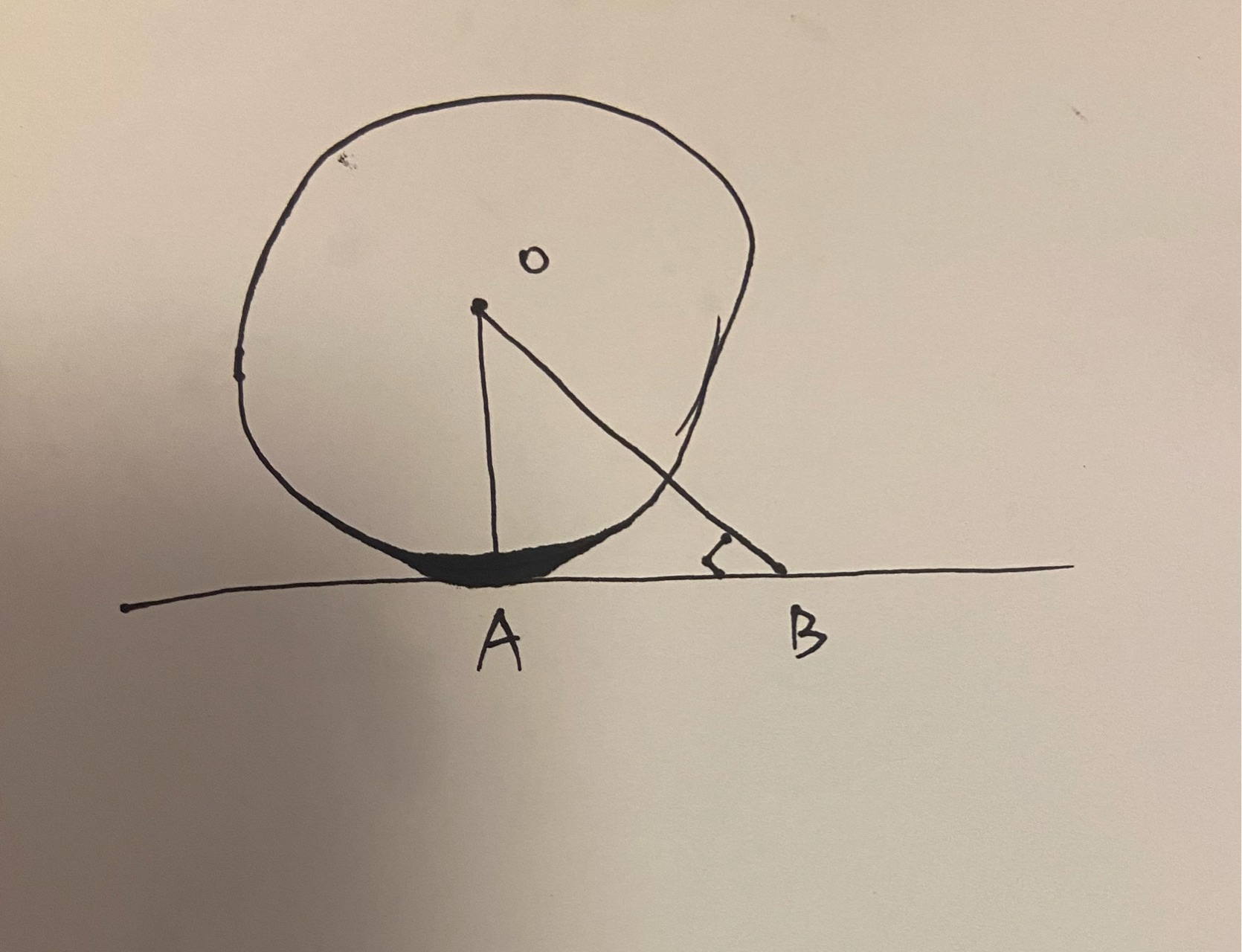切线专题

从“法线贴图的意义”到“切线空间公式的推导与验证”

目录目标1. 法线贴图1.1 “法线”的意义1.2 “法线贴图”的意义 2. 切线空间2.1 法线贴图中数据的含义2.2 “切线空间”的定义 3. 切线空间计算公式3.1 构造几何关系等式3.2 切线空间计算公式 4. 代码5. 验证——与其他美术软件计算的结果进行比较总结目标本篇的重点是讨论法线贴图的意义讨论切线空间的意义推导切线空间的计算公式根据公式编写代码将其计算

$数学基础：切线和变化率$

数学基础：切线和变化率

我们将看看微积分研究中两个相当重要的问题。现在关注这些问题有两个原因。第一个问题：切线我们要研究的第一个问题是切线问题。在讨论这个问题之前，最好定义一条切线。函数的切线f(x)在点上x=1，是一条刚好在相关点接触函数图形的线，并且与该点的图形“平行”（以某种方式）。请看下面的图表。 from manim import * class TangentLineScene01(Scene

寻找切线

1687 : 寻找切线描述给定平面上N个点P1=(X1, Y1), P2=(X2, Y2), … PN=(XN, YN)。请你从中找到两个不同的点Pi和Pj满足：其他所有点都在Pi和Pj连线的同一侧(可以在连线上)。如果有多组答案满足条件，你可以输出任意一组。输入第一行包含一个整数N。以下N行每行包含两个整数Xi和Yi。对于50%的数据，1 ≤ N ≤

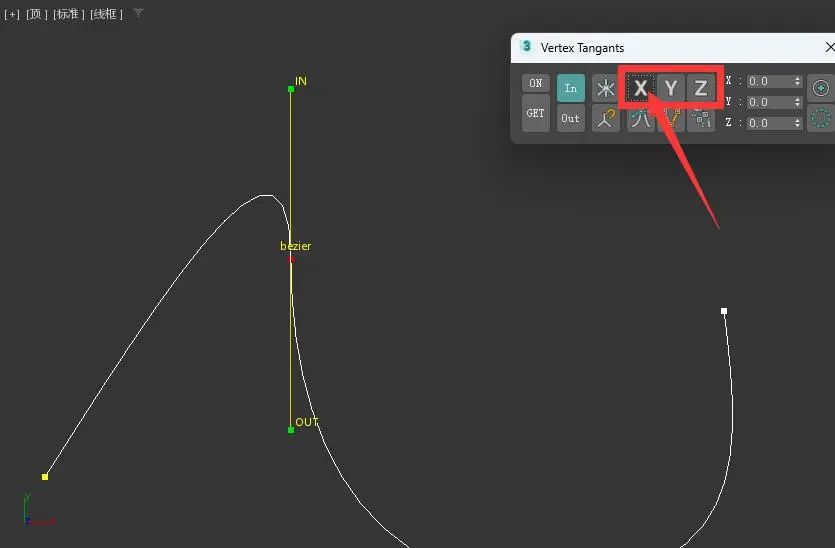
沐风老师3DMAX顶点切线控制插件VertexTangants安装使用方法

3DMAX顶点切线控制插件VertexTangants安装使用方法 3DMAX顶点切线控制插件VertexTangants，用于轻松控制图形顶点切线的工具。【主要功能】 -脚本具有获取选定顶点的自动检测功能，您可以随时使用“获取按钮”获取选定顶点。 -有一个用于激活撤消的ON按钮（如果未激活，则不会记录撤消），因为更改切线位置在3d

Maya: 菜单编辑曲线投影切线

编辑曲线 >投影切线可以改变曲线端点处的切线方向，使其与两条相交曲线或与一条曲面的切线方向保持一致。

[OpenGL] opengl切线空间

目录一引入二 TBN矩阵三代码实现 3.1手工计算切线和副切线 3.2 像素着色器 3.3 切线空间的两种使用方法 3.4 渲染效果四复杂的物体本章节源码点击此处继上篇法线贴图来熟悉切线空间是再好不过的。对于法线贴图来说,我们知道它就是一个2D的颜色纹理,根据rgb来映射法线对应的xyz,从而达到在同一个平面上有多个不同方向法线的效果，这样就能根据

漫步微积分三——如何计算切线的斜率

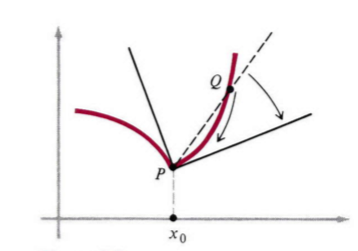
各种想法都有自己的一席之地，但是时间会剔除许多细节。 P＝(x0,y0) P＝(x_0,y_0)是抛物线 y＝x2 y＝x^2上的任意一个定点，如图1所示。作为基本思想的第一个图例，给定抛物线上一点 P P，计算切线的斜率。首先，我们选择曲线上的一个临近点Q=(x1,y1)Q=(x_1,y_1)。接下来，我们画出由这两点确定的割线 PQ PQ，割线的斜率明显是： msec=slope o

Threejs用切线实现模型沿着轨道行驶

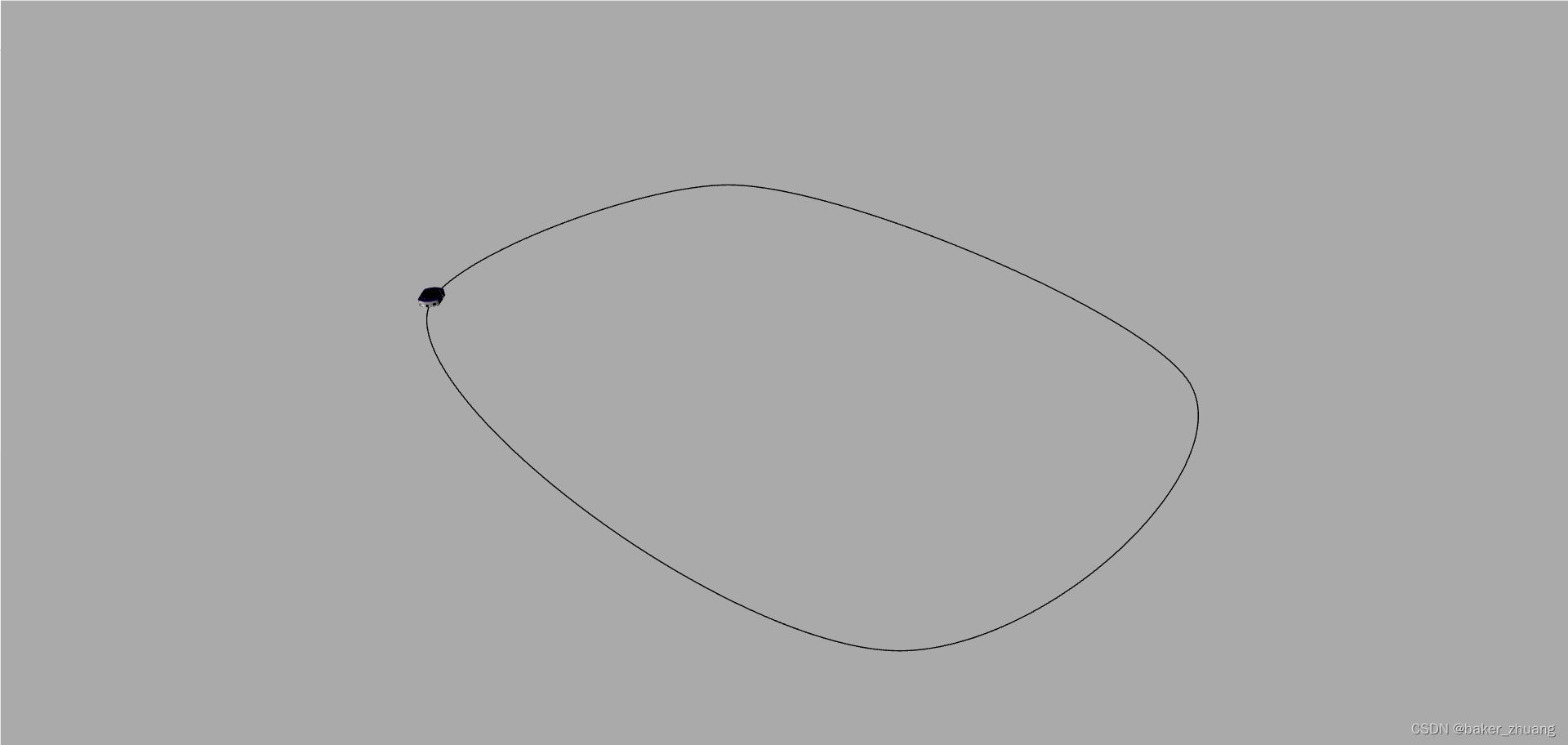
这次讲一个经常遇到的使用场景，让模型沿着轨迹运动，这个场景需要解决两个问题，第一是让模型沿着轨迹运动，第二是在沿着轨迹运动的同时，要保持模型的头部也时刻保持前方，而不是单纯的只是更新模型位置。还是先创建一个场景，添加相机，灯光，渲染器等，然后需要创建一个轨迹，这里用CatmullRomCurve3创建一个3维曲线，这个的好处是等会可以将此曲线拆解成多个同等份的点

导数和梯度，切线和法向量

转自：http://www.cnblogs.com/jerrylead/archive/2011/03/09/1978280.html 作者讲得很清楚记得在高中做数学题时，经常要求曲线的切线。见到形如之类的函数，不管三七二十一直接求导得到，这就是切线的斜率，然后就得到了处的切线。上大学又学习了曲面切线和法向量的求法，求偏导是法向量，然后套公式求出切线。一个经典例子如

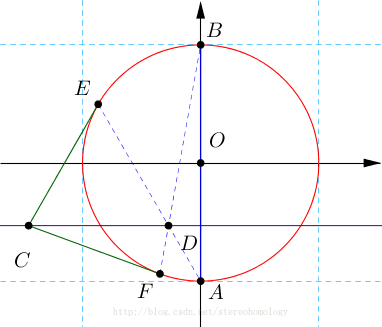
[matlab]过一点与椭圆的切线

最近用到二次曲线切点的知识，在丘维声老师的《解析几何》一书上找到一些公式，在计算机视觉中书上也有相关的介绍。配极映射：若p是曲线C上一点，则 l=Cp确定平面上一条直线。若p是曲线C外一点，则过点p的两条切线 l与m 所构成的退化二次曲线的矩阵表示为 T=[p]x inv(c) [p]x = l'm+m'l 配极对应：给定一条二次曲线C，对平面上

平面解析几何----切线交点和焦点的连线平分焦点和弦的张角

射影几何----过双曲线上一点P的切线交双曲线于AB两点则PA=PB

过双曲线上一点P的切线交双曲线于AB两点则PA=PB

证明：切线垂直于半径

证明：切线垂直于过切点的半径。下面是网上最简单的证明方法。证明：利用反证法。如下图所示，直线AB和圆O切于点A，假设OA 不垂直于 AB，而 O B ⊥ A B OB \perp AB OB⊥AB，则 ∠ O B A = 90 ° \angle OBA = 90 \degree ∠OBA=90°，根据勾股定理可得斜边最长，即边OA>边OB ，但是实际上直线和圆的交点只有一个交点A，

参数方程求导（常与切线方程法线方程连考）

方法一般形带值参数方程求切线方程，法线方程

让微积分穿梭于工作与学习之间（17）：圆弧直线在端点处的切线及其在趋于直线时的极限

对CAD圆弧直线不了解的朋友可以先阅读以下博文： https://blog.csdn.net/iloveas2014/article/details/103837857 https://blog.csdn.net/iloveas2014/article/details/103848611 在上篇的末尾，我提到了线条端点处的切线在寻找封闭图形中的重要性，但没给出任何解释，为此我转发一篇博文。

ghpython_起点、终点、起点切线绘制圆弧

今天继续聊rhinopython101里的案例，根据起点、终点、起点切线绘制圆弧，其实这种绘制圆弧的方式，在现在的ghpython里的rhinoscriptsyntax模块已经有了这种方法，这里，咱们主要是学习编程的思路、内在逻辑和敲代码的肌肉训练。 1.构建由起点指向中点的向量，并将其单位化； 2.将起点的切线向量也进行单位化； 3.将以上两个单元向量求和，并将求和后的向量单位化； 4.将相加

一道切线和圆有关的几何证明题及解析解答

原题已知，如图， AB 是 ⊙O 的直径， CE 、 CF 是 ⊙O 的两条切线， D 是 AE 和 BF 的交点。求证： AB⊥CD 画出来动态调整图观察，结论没有问题。只是纯几何的证明太难。证明解析的方法是现成的，像是中学可以理解的。只是过程很繁琐，所以，证明一下。不失一般性（这个说法很酷），假设问题中的圆是单位

专题：平面、空间直线参数方程下的切线斜率问题

本文研究平面、空间直线在参数方程形式下，切线斜率（即导数）如何表示的问题。如上图所示。设 y = f ( x ) ， x = φ ( t ) ， y = ψ ( t ) 当 t = t 0 时， x = x 0 ， y = y 0 ，即点 A 坐标为 ( x 0 , y 0 ) 点 A 处的导数 f ′ ( x 0 ) = lim ⁡ Δ x → 0 Δ y Δ x = lim ⁡ Δ t