让微积分穿梭于工作与学习之间（17）：圆弧直线在端点处的切线及其在趋于直线时的极限

对CAD圆弧直线不了解的朋友可以先阅读以下博文：

https://blog.csdn.net/iloveas2014/article/details/103837857

https://blog.csdn.net/iloveas2014/article/details/103848611

在上篇的末尾，我提到了线条端点处的切线在寻找封闭图形中的重要性，但没给出任何解释，为此我转发一篇博文。

https://blog.csdn.net/keng_s/article/details/67102867

大家在阅读的过程中可以看到其中的一步是要对线条进行角度排序。对于直线线段来说，角度取两点的连线即可，而曲线则不能再取连线了。大家看下面的图。

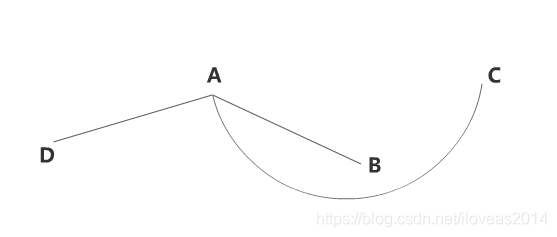
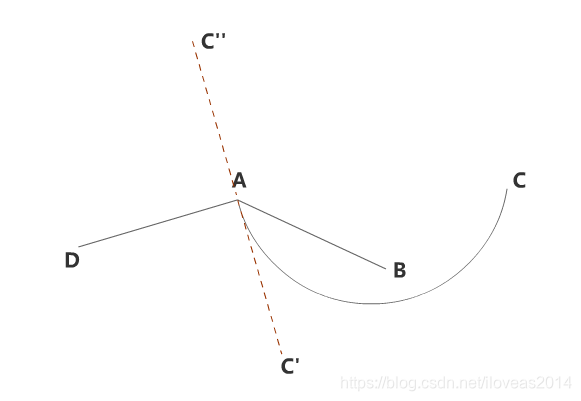
我们想要把AB，弧AC，AD三条线在A端点处按顺时针排序，正确的结果是AB，AC，AD，但若用连线AC来作为排序依据的话，那么顺序就变成AC，AB，AD了。

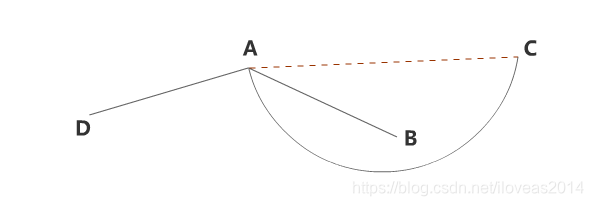
所以要改用弧AC在A点处的切线AC'来计算角度，如下图所示。

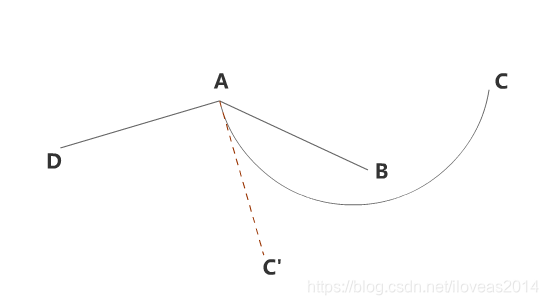
下面我们来尝试计算圆弧直线在端点上的切线斜率，显然当圆弧的凸度趋于0时，圆弧变为直线，切线跟连线的方向一致，如下面的动图所示。

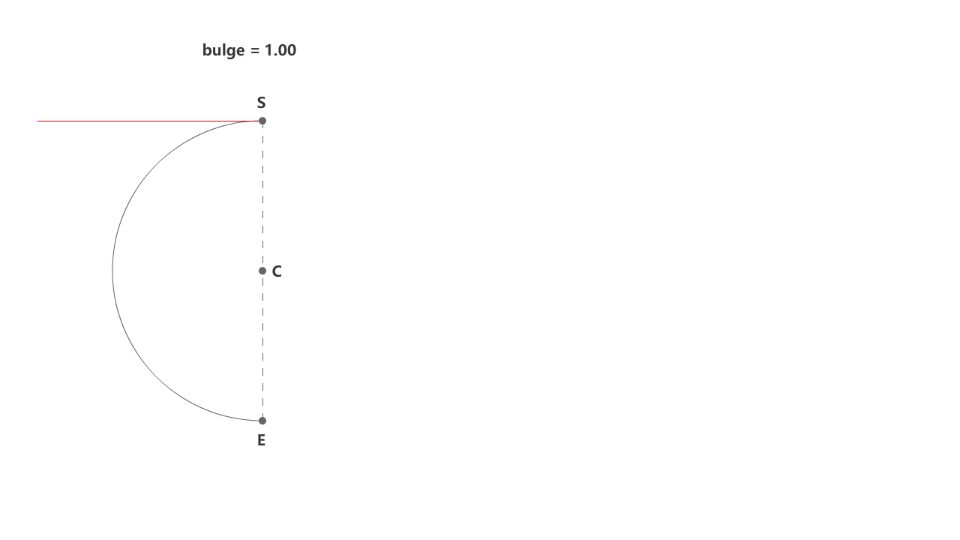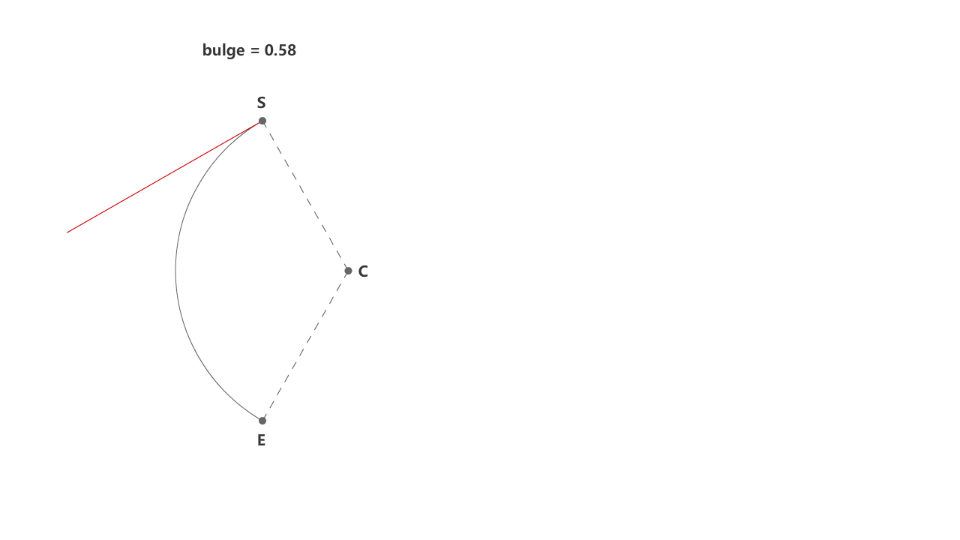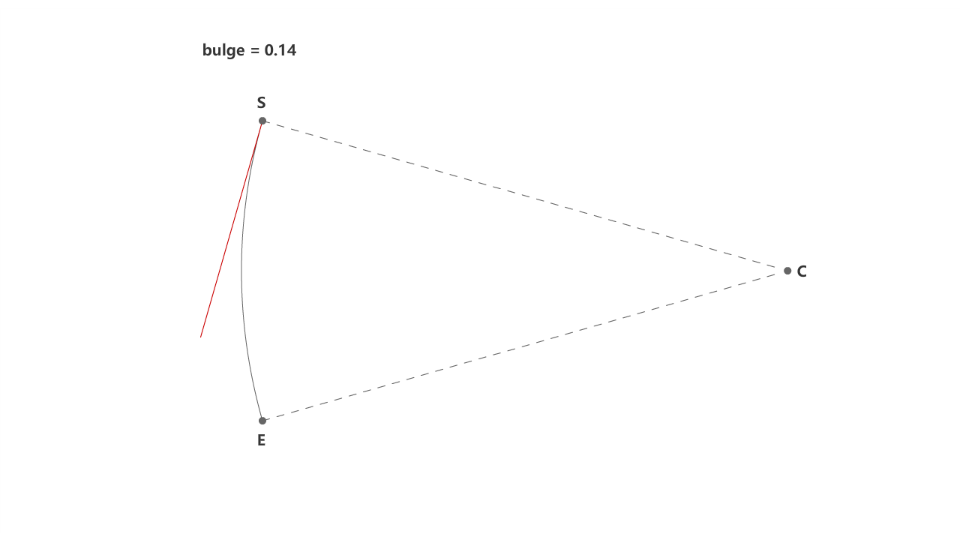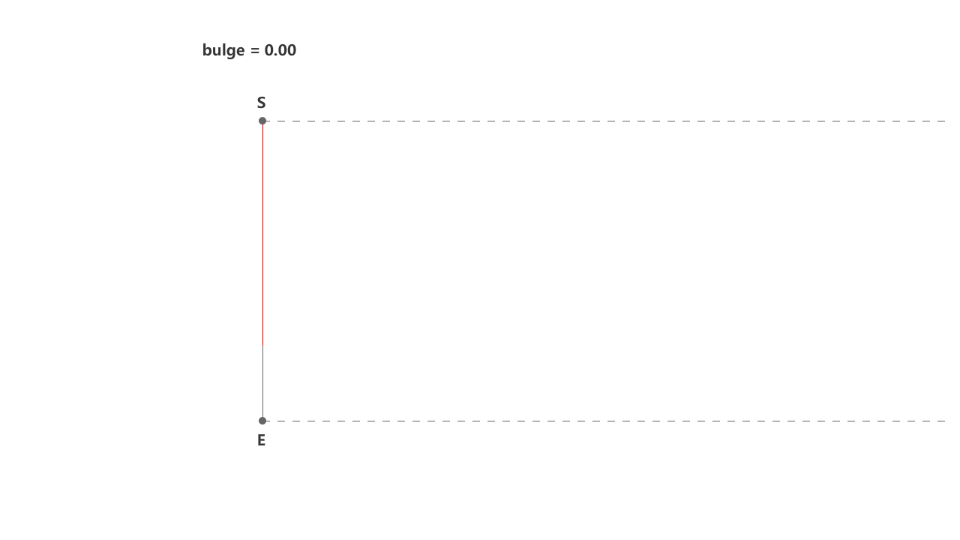
求切线斜率，相信大家都会想到用求导的方法，不过圆弧是多值函数，所以计算的方法也特殊一些。

总的来说，要计算这种曲线的切线及其趋于直线时的极限，我想到的方法有3种：

1 利用圆弧切线的几何性质——跟切点上的半径垂直进行计算，然后计算bulge趋于0时的极限

2 对圆弧直线的一般方程进行隐函数的求导

3 把圆弧直线的一般方程看作二元函数，然后求出其偏导数，再根据以下公式求得y对x的导数

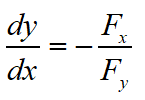
方法2和方法3其实都是隐函数的求导，只是3更为简便，同时也更难理解，毕竟涉及了二元函数。

此处我们使用方法2。感兴趣的朋友可以自行用方法1或者方法3来推导，也可以留言跟我讨论。

我们把二元二次方程的一般式搬过来，在最普通的情况下进行求导。然后，圆和直线都不包含xy项，可以省略

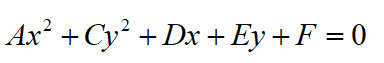
两侧对x进行求导，得到

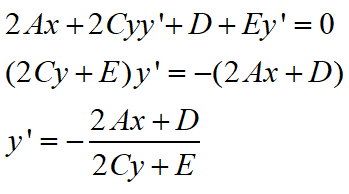
然后我们把圆弧曲线中对应的系数代进去

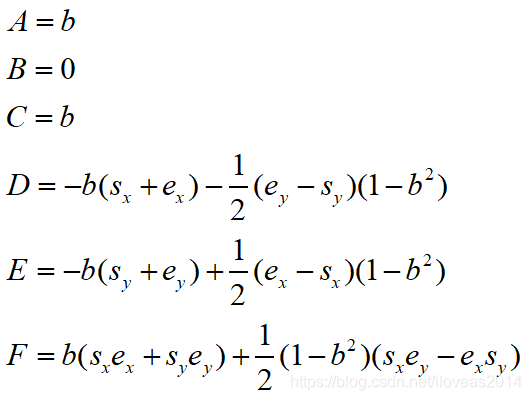
至此，圆弧直线在线上任一点(x,y)的切线斜率就算出来了。

然而这个式子还是蛮复杂的，但是我们用得最多的一般都是起点和终点，那么我们分别把(sx，sy)和(ex，ey)代进去算一下。

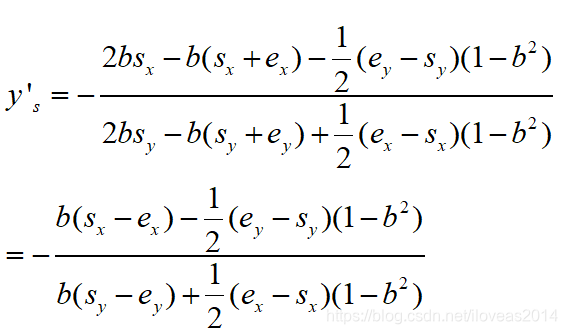
看着还是蛮复杂，但是起点和终点都是常量，因此在编程的时候我们可以把起点和终点的差值用一个向量(Δx,Δy)存起来从而让代码更清晰。那么这里的公式也能简写为

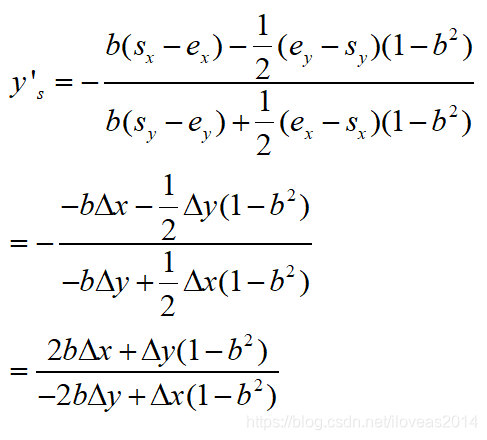
这样就简洁多了，类似地，终点的导数结果为

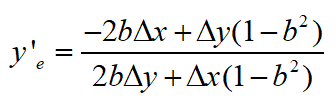
y's，y'e这两个导数值的意义是圆弧在S和E处的切线斜率，如下图的红线和蓝线所示。

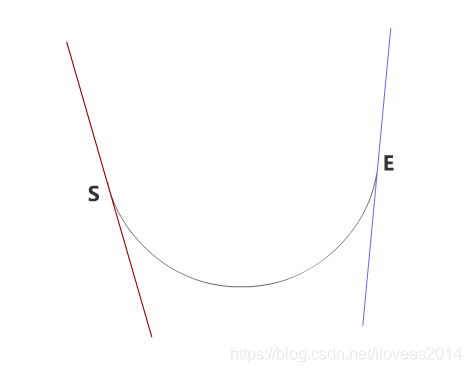
然后我们算一下它们在b趋于0的时候等于多少。

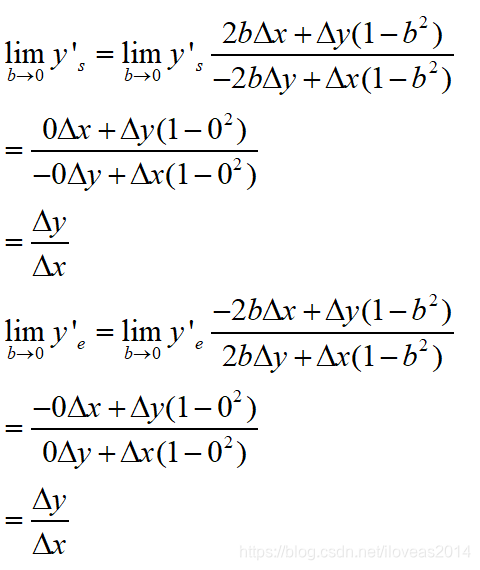
它们在凸度趋于0的时候都等于起点和终点连线的斜率，跟我们的期望完全一致。

然而问题并没到此结束，因为算出来的切线没有方向，而进行角度排序的时候我们需要给出的是指定方向的切线向量，如下图所示，我们要的是AC'和水平线的夹角而非AC''

切线斜率并没有给出它们的方向，所以在项目里我用的是方法1，从而更好地对x和y的方向分别进行把控。

那么此处我就不在推导的情况下给出切线向量的结果，其实只是把导数结果拆出来，并且根据不同情况对xy给出不同的符号

起点的切线向量为

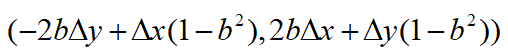
终点的切线向量为

跟导数的分子分母对照下，可以发现，起点刚好是把分子分母拆开，而终点则是把分子分母拆开后再分别取反。所以说这地方其实还是存在着很微妙的规律，就留给读者们慢慢品味了。

下篇我会给大家讲解圆弧直线的等分公式及其在趋于直线时的极限，敬请期待！