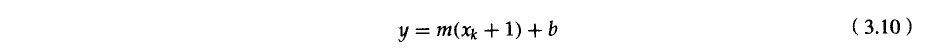直线专题
POJ1269 判断2条直线的位置关系
题目大意:给两个点能够确定一条直线,题目给出两条直线(由4个点确定),要求判断出这两条直线的关系:平行,同线,相交。如果相交还要求出交点坐标。 解题思路: 先判断两条直线p1p2, q1q2是否共线, 如果不是,再判断 直线 是否平行, 如果还不是, 则两直线相交。 判断共线: p1p2q1 共线 且 p1p2q2 共线 ,共线用叉乘为 0 来判断, 判断 平行: p1p
求空间直线与平面的交点
若直线不与平面平行,将存在交点。如下图所示,已知直线L过点m(m1,m2,m3),且方向向量为VL(v1,v2,v3),平面P过点n(n1,n2,n3),且法线方向向量为VP(vp1,vp2,vp3),求得直线与平面的交点O的坐标(x,y,z): 将直线方程写成参数方程形式,即有: x = m1+ v1 * t y = m2+ v2 * t
n条直线最多能划分出多少个平面?
N条直线,两两相交,其交点各不不同,则产生的交点数目为N个数中取2个数的组合; 同时,也只有这种情况下(两两相交,也交点不同),分割的平面数最多, 数目为: 2 + (N-1)(N+2)/2. 这里求最少平面数没有意义,因为最少平面数就是N+1, 即N条直线两两平行的时候,分割的平面最少。 举例: 1条直线分割平面数最多为2; a1 = 2 2条直线分割平面数最多为4;
OpenCV绘图函数(12)绘制直线函数 line()的使用
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C++11 算法描述 line 函数在图像中绘制从 pt1 到 pt2 两点之间的线段。这条线会被图像边界裁剪。对于没有抗锯齿效果且坐标为整数的线,会使用 8-连接或者 4-连接的 Bresenham 算法。粗线条的绘制会采用圆角处理。抗锯齿线条则通过高斯滤波来绘制
Codeforces Round #329 (Div. 2) B. Anton and Lines ([好题] 计算直线在区间是否有交点)
题目链接 题意:给出n个条直线,然后在指定的区间(x1,x2)是否有直线的交点存在。 解法:一:闭区间,首先把区间略微调小。 二:计算直线在x1,x2上的交点y坐标,以及直线的id,然后按照y值,id值排序,最后判断第x1,x2左右两边的第i个点是不是同一直线的,如果不是,就存在交点。 #include<bits/stdc++.h>using namespace std;const i
Unity坐标系计算3D中两直线的最短距离及最近点的几何原理
方法1: 已知空间中两直线AB, CD,判断它们是否相交 问题的关键是求出这两条直线之间的最短距离,以及在这个距离上最接近两线的点坐标,判断该点是否在直线AB和直线CD上。 首先将直线方程化为对称式,分别得到两直线方向向量AB=(x1,y1,z1), CD=(x2,y2,z2),再将两向量AB, CD叉乘得到其公垂向量N=(x,y,z),在AB, CD两直线上分别选取点E
这神器好棒!阅读体验直线飙升~
这是蜗牛互联网的第 89 期原创。 作者 | 白色蜗牛 来源 | 蜗牛互联网(ID: woniu_internet) 转载请联系授权(微信ID: 919201148) 前言 我们在网上阅读的时候,经常会看到一些有价值的观点或者是有用的知识,希望可以摘录下来,甚至把我们自己当时的思考也记录下来,以便未来需要的时候回头再看。 有的朋友可能会记到一个小本本上,有的朋友可能会写到线上的笔记软件里。但
【Opencv】Hough变换找直线和圆
目录 题目 解决方法 完整代码 Hough参数详解 总结 参考 题目 用霍夫变换找出图像中的直线和圆(用彩色直线和圆标记在原图上)。要求有代码,有注释,有过程、有结果 解决方法 # -*- coding: UTF-8 -*-import cv2import numpy as np# 1.加载图片,转为二值图img = cv2.imread('image.j
BNU 7536 HDU 3425 Coverage (圆与直线相交 )TeamContest - 4—B【解题报告】
【题目链接】click here~~ 【题目大意】求多个圆与线段相交的部分占整个线段的百分比。 【解题思路】 此题首先要判断圆心不一定全在给定的线段上,可以在任意的位置,(理解错了题,原先以为圆心在线段上,读题要仔细!) 因此我们可以联立圆的方程和线段的方程首先判断线段与圆有没有交点 求出方程组解得: 二次项系数为 a = cos(cx1,cx0) +cos(cy1,cy0);//二次项的
LN2054Y42AMR 具有热调节功能的独立直线锂离子电池充电器
一般说明 LN2054是一款为单节锂离子电池设计的完整恒流/恒压线性充电器。其ThinSOT封装和外部元件数量少,使LN2054最适合便携式应用。此外,LN2054专门设计用于在 USB 电源规格内工作。 由于内部 MOSFET架构,不需要外部感测电阻,也不需要阻塞二极管。热反馈调节电荷电流,以限制高功率运行或高环境温度下的管芯温度。电荷电压固定在4.2V,电荷电流
MATLAB 快速计算点到二维直线的距离并可视化(79)
计算点到二维直线距离,主要是还提供了具体的可视化方法 MATLAB 快速计算点到二维直线的距离并可视化(79) 一、算法介绍二、算法实现1.代码2.效果 一、算法介绍 问题:给定一条直线的方程 (Ax + By + C = 0) 和一个点 ((x_0, y_0)),点到直线的距离 (d) 方法:运行此脚本后,您将在 MATLAB 中看到一条红色的直线(倾斜 45
POJ 1269 Intersecting Lines(判断直线相交)
题目地址:POJ 1269 直接套模板就可以了。。。实在不想自己写模板了。。。写的又臭又长。。。。不过这题需要注意的是要先判断是否有直线垂直X轴的情况。 代码如下: #include <iostream>#include <cstdio>#include <string>#include <cstring>#include <stdlib.h>#include <math.h>
判断两条直线的位置关系
最近在看任意两个多边形的交并比。 开始自己想办法,花了两天时间,进展比较缓慢。情况越想越多,越来越不可控。于是只有求助与度娘了。虽然还是有些问题,但问题还是慢慢的有些好转,其中一点心青大神的博客中提到的想法和源码,给了我很大启示。 求两条直线的位置关系中, 大神是用的向量的想法,思路很新颖,但是我有点一知半解,c++转的python代码运行也有点问题, 于是我老老实实的在网上补习了一下直线的位置关
直线一级倒立摆微分建模
建模内容如下: https://mp.weixin.qq.com/s?__biz=Mzg5OTIyNDEzMg==&mid=2247483673&idx=1&sn=c4e8024ebffd87611b757f7fd570f3c4&chksm=c057c632f7204f2442d0aab652847e342447fa604f04d74faafb798f022fb30e
OpenGL:中点直线算法
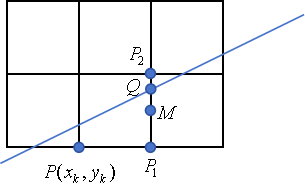
理论部分 中点直线算法是通过在像素中确定与理想直线最靠近的像素来进行扫描转换的。 在上图中,假设直线的斜率 0 ≤ m ≤ 1 0\le m \le 1 0≤m≤1。假设当前最近的像素已经确认为 P ( x k , y k ) P(x_k, y_k) P(xk,yk),由于 x x x位最大的位移方向,因此直线在 x x x方向上每次增加一个像素单位,而在 y y y方向上是否
二维坐标中在一条直线上最大点数
import java.util.HashMap;class Point {int x;int y;Point() { x = 0; y = 0; }Point(int a, int b) { x = a; y = b; }}public class Solution {//解法一:存在问题public int maxPoints(Point[] points) {if(points==nu
HALCON-从入门到入门-霍夫识别直线
1.废话 霍夫变换是一种特征检测,被广泛应用在图像分析、计算机视觉以及数位影像处理。霍夫变换是用来辨别找出物件中的特征,例如:线条。他的算法流程大致如下,给定一个物件、要辨别的形状的种类,算法会在参数空间中执行投票来决定物体的形状,而这是由累加空间里的局部最大值来决定。 现在广泛使用的霍夫变换是由RichardDuda和PeterHart在公元1972年发明,并称之为广义霍夫变换,广义霍夫
永磁同步直线电机(PMLSM)控制与仿真4-永磁同步直线电机数学三环闭环控制仿真
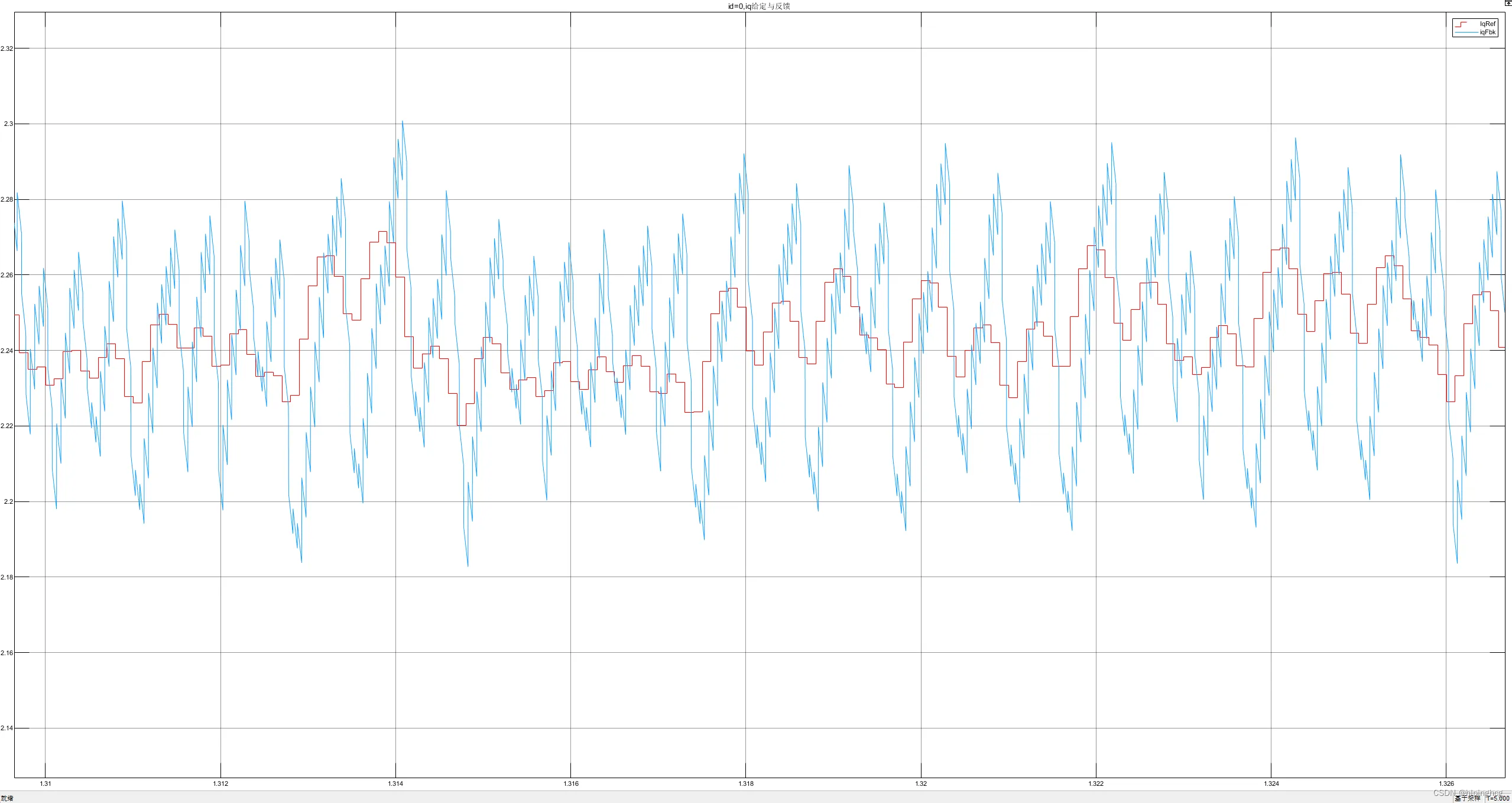
文章目录 1、参数设置及脚本2、相电流波形3、位置波形4、速度波形5、控制电流波形6、永磁同步直线电机在实际控制中如何控制参考 写在前面:原本为一篇文章写完了永磁同步直线电机数学模型介绍,永磁同步直线电机数学模型搭建,以及永磁同步直线电机三环参数整定及三环仿真模型搭建,但因为篇幅较长,所以分开写。 永磁同步直线电机数学模型 永磁同步直线电机数学模型搭建 永磁同步直线电机数学三环控制
Bresenham绘制直线学习笔记
今天学习计算机图形学第三版,使用Bresenham绘制直线,有一些公式推导的不是很细致,自己推导了一番,记录一下,方便自己日后学习。 疑惑点: 参考图: 推导过程: 又因为: P0 = 2 * DeltaY * x0 - 2 * DeltaX * y0 + 2 * DeltaY + DeltaX*(2b - 1) 因为: 所以 2 * b * DeltaX =
永磁同步直线电机(PMLSM)控制与仿真3-永磁同步直线电机数学三环控制整定
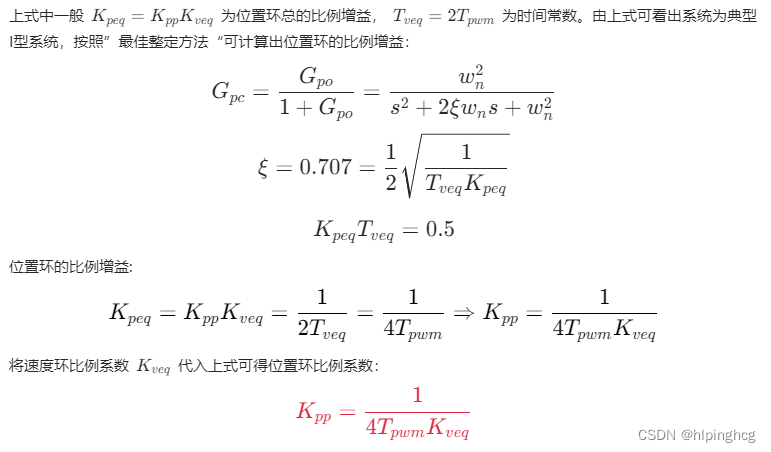
文章目录 1、电流环参数整定2、速度环参数整定3、位置环参数整定 写在前面:原本为一篇文章写完了永磁同步直线电机数学模型介绍,永磁同步直线电机数学模型搭建,以及永磁同步直线电机三环参数整定及三环仿真模型搭建,但因为篇幅较长,所以分开写。 永磁同步直线电机数学模型 永磁同步直线电机数学模型搭建 永磁同步直线电机数学三环控制整定 永磁同步直线电机数学三环闭环控制仿真 1、电流环参
永磁同步直线电机(PMLSM)控制与仿真2-永磁同步直线电机数学模型搭建
文章目录 1、公式总结2、电压方程模型3、运动方程4、推力方程5、转化关系 写在前面:原本为一篇文章写完了永磁同步直线电机数学模型介绍,永磁同步直线电机数学模型搭建,以及永磁同步直线电机三环参数整定及三环仿真模型搭建,但因为篇幅较长,所以分开写。 永磁同步直线电机数学模型 永磁同步直线电机数学模型搭建 永磁同步直线电机数学三环控制整定 永磁同步直线电机数学三环闭环控制仿真 直线电




![Codeforces Round #329 (Div. 2) B. Anton and Lines ([好题] 计算直线在区间是否有交点)](/front/images/it_default.jpg)