一道切线和圆有关的几何证明题及解析解答

原题

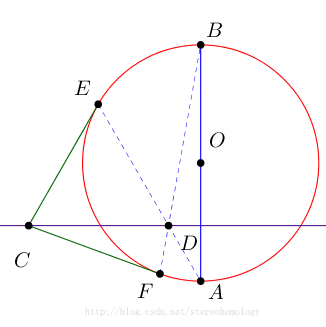
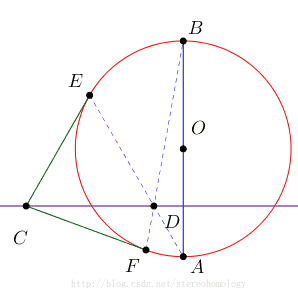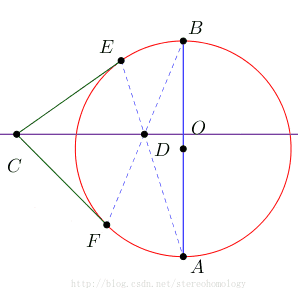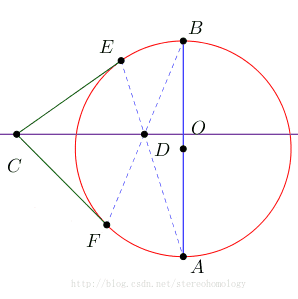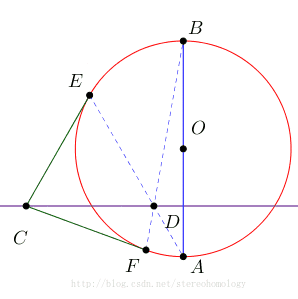
已知，如图， AB  是  ⊙O  的直径， CE 、 CF  是  ⊙O  的两条切线， D  是  AE  和  BF  的交点。

求证：  AB⊥CD

画出来动态调整图观察，结论没有问题。只是纯几何的证明太难。

证明

解析的方法是现成的，像是中学可以理解的。 只是过程很繁琐，所以，证明一下。

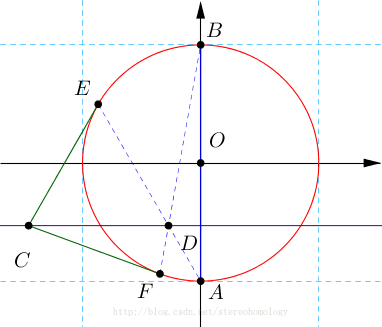
不失一般性（这个说法很酷），假设问题中的圆是单位圆、以圆心为原点建立平面直角坐标系，让直径  AB 在纵坐标轴上，从而，两个点的坐标：  A(0,−1),B(0,1) 。

假设单位圆 ⊙O  上两个切点的坐标  E(cosθ1,sinθ1),F(cosθ2,sinθ2) ， 则容易知道直线：

CE 的斜率  −cotθ1 ,  CF  的斜率  −cotθ2 。 两直线方程可以由点斜式改写为更一般的形式，联立如下：

联立可以求出  C  的纵坐标： 

进一步，通过两点式表示方法并转化，可以得到另外两条直线， AE  和  BF  的方程的一般形式，注意到  A 、 B  的坐标都很简单，方程也不复杂：

类似解出  D  点纵坐标，发现刚好等于  C  的纵坐标。

所以，  CD  跟所建立坐标系中的纵坐标轴垂直， 也就是跟  AB  垂直。解析方法，把几何里面的直线间垂直，转化成两个二元一次线性方程组之间有一个特定解(的解析形式)恒等。

求解和化简繁琐，关键是证明两者相等即可，线性方程组的解因此无须是最简形式。上面只能用于对答案了。

纯几何的证明如果能够利用射影几何的一些定理可行性会大大增加。有些超纲，但是在数学竞赛和自主招生考试中未尝不可。