证明题专题
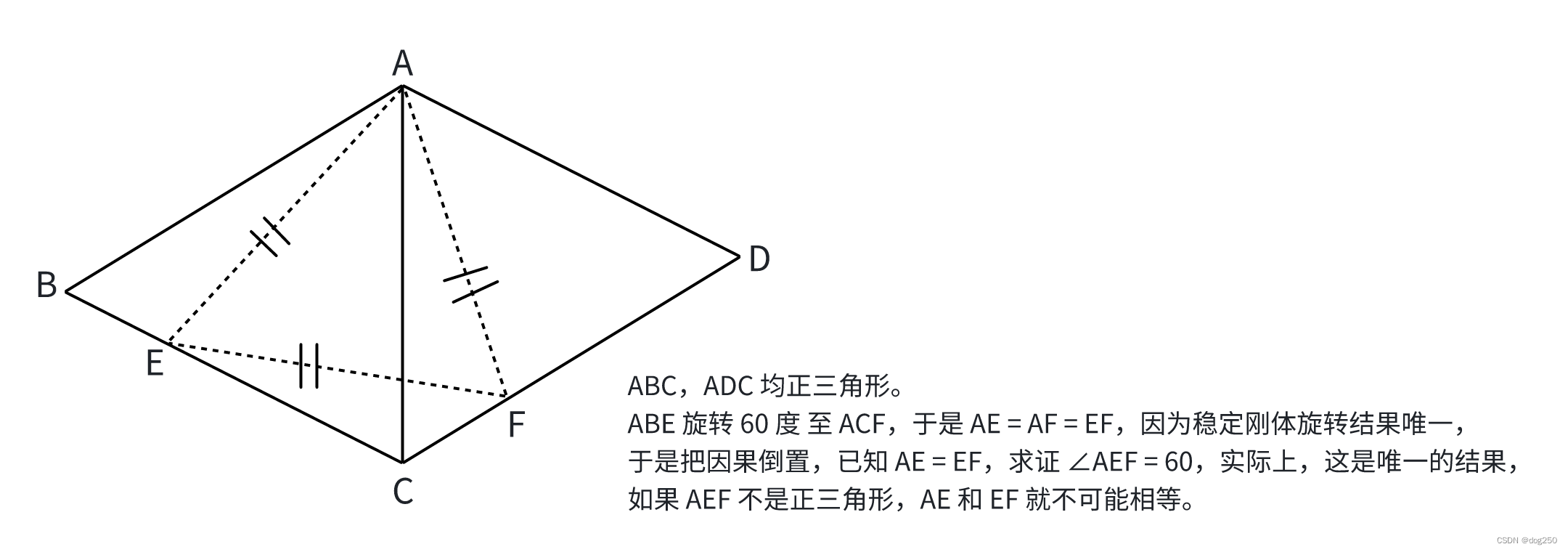
一道全等三角形证明题
接着上次那道题 一道初中一年级几何题解析,再来做一道初中一年级下半学期几何题目: 傍晚丢垃圾散步时看到小小的学生学习群里丢了这个题目,想到一个解法。实在构造不出契合题干阅读材料结论的三角形,索性先根据这结论做一个推论: 然后再根据这推论进一步证明: 大概就是这个意思。 这种传统解法我一向视作奇技淫巧而嗤之以鼻,这道题其实就是一个稳定刚体旋转,若要问 ∠BEF 等于多少,大多数
离散数学-代数系统证明题归类
什么是独异点? 运算° 在B上封闭,运算° 可结合,且存在幺元。 学会合理套用题目公式+结合律 零元? 群中不可能有零元 几个结论要熟记: 1.当群的阶为1时,它的唯一元素视作幺元e 2.若群的阶大于1时,且同时存在幺元和零元的话,幺元不等于零元 纯个人理解: 因为零元和什么相乘,依旧是零元。 而零元又不等于幺元。 我们知道,一个
最长线段(几何证明题)
最长线段(chord.pas/chord.in/chord.out) (LYOI信息学综合模拟20090321Problem 1) 问题描述 给定两个圆各自的圆心坐标和半径长。过其中一个交点作直线,该直线与圆的另外两个交点分别为A、B。线段AB最长是多少? 输入数据 第一行有三个用空格隔开的整数x1,y1,r1,依次表示第一个圆的圆心坐标和半径; 第二行有三个用空格隔开的整数x2,y2
求斐波那契前n项平方和 ——矩阵快速幂模板(几何构造证明题【附图】)
根据图示,我们可以知道:后面的大正方形的边长总是等于前面的小正方形组成的矩形的长;前面几个斐波那契数的平方之和(也就是前面几个小正方形的面积之和)在数值上等于最后出现的一个和下一个紧接着未出现的斐波那契数的乘积(也就是已经出现的小正方形组成的矩形的面积等于其中最大的一个小正方形的边长乘以下一个紧接着未出现的正方形的边长)。对应的公式化简后如下: #include <bits/stdc++.
一道切线和圆有关的几何证明题及解析解答
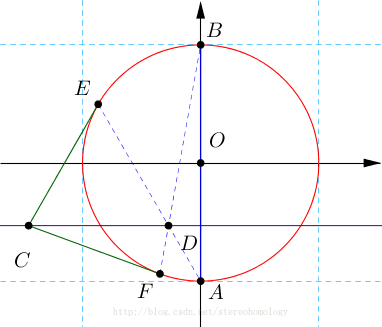
原题 已知,如图, AB 是 ⊙O 的直径, CE 、 CF 是 ⊙O 的两条切线, D 是 AE 和 BF 的交点。 求证: AB⊥CD 画出来动态调整图观察,结论没有问题。只是纯几何的证明太难。 证明 解析的方法是现成的,像是中学可以理解的。 只是过程很繁琐,所以,证明一下。 不失一般性(这个说法很酷),假设问题中的圆是单位