本文主要是介绍一道全等三角形证明题,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
接着上次那道题 一道初中一年级几何题解析,再来做一道初中一年级下半学期几何题目:
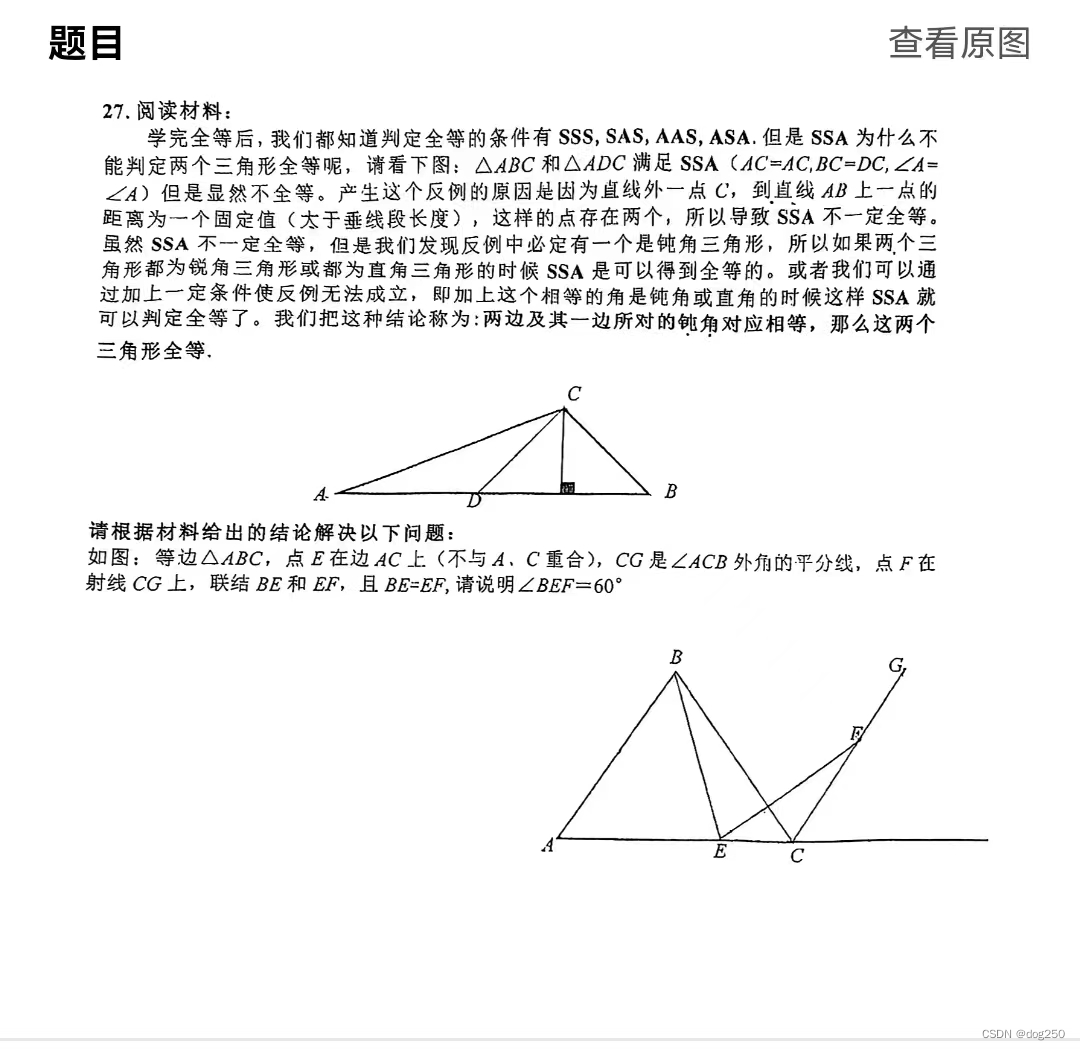
傍晚丢垃圾散步时看到小小的学生学习群里丢了这个题目,想到一个解法。实在构造不出契合题干阅读材料结论的三角形,索性先根据这结论做一个推论:
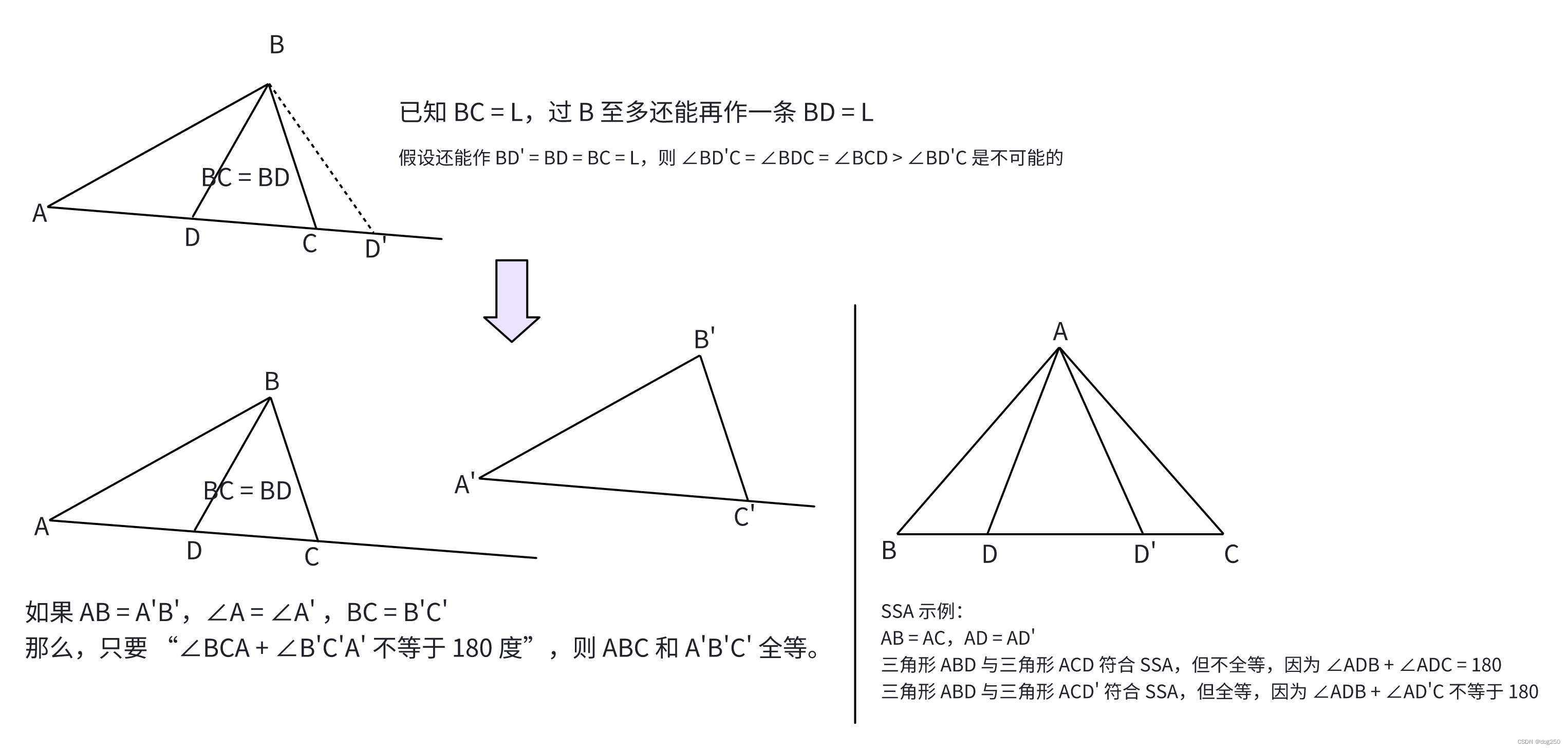
然后再根据这推论进一步证明:

大概就是这个意思。
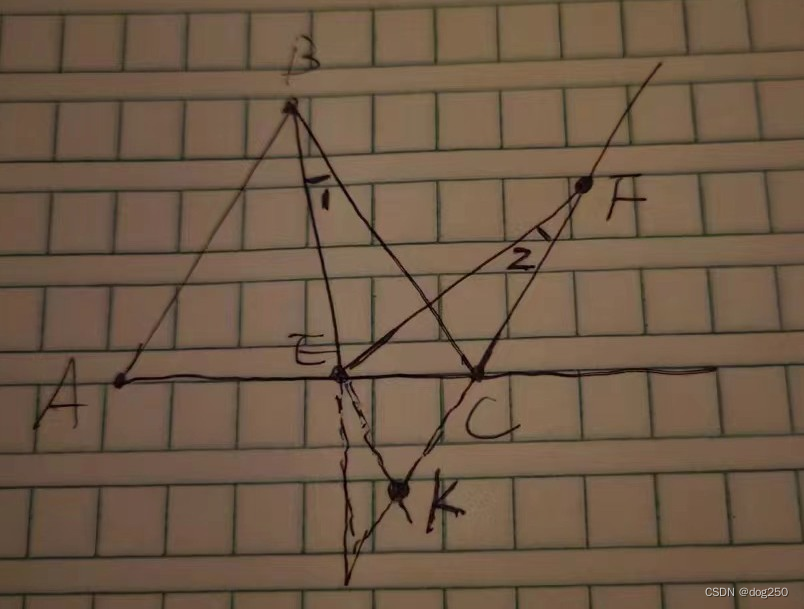
这种传统解法我一向视作奇技淫巧而嗤之以鼻,这道题其实就是一个稳定刚体旋转,若要问 ∠BEF 等于多少,大多数人都有能力毫无犹疑回答 60,但出题人非要将大家往奇技淫巧方面引导。
即便辅助线和传统解法完全一致,它还是一个旋转问题,而无关全等三角形:
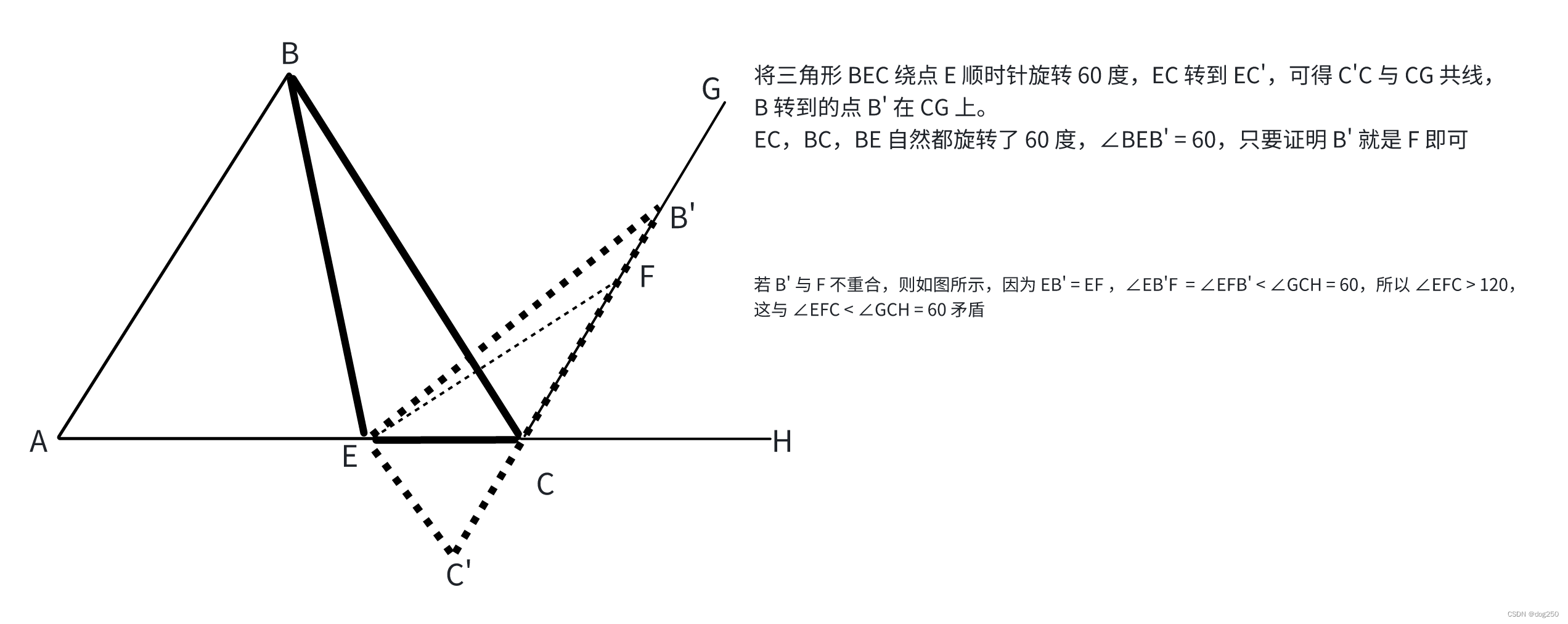
所谓证明,只要把结果逼到 “不得不如此”,就可结束了,但我们现在并不用这理念来实施教育,我们强调用学过的 “知识点” 去映射问题,这也难怪如果没有学过某个知识点,就很难推进问题的解决。
以本文展示的问题为例,若要用全等三角形的知识点,就要至少构造两个三角形,而上面那图里 CK = CE 就是颇具哇塞的奇技淫巧,但看下面这图,K 点其实什么也不是,它就是 C 点自然旋转而来的 C’,就一个普通旋转,一下子那些辅助线就全部暴露出来了,我将那些点命名为 C’,B’,看起来就不是奇技淫巧而是旋转操作了。
初中几何,所有涉及全等三角形的,都可以通过平移,旋转,对折加反证法搞定,这是基本,我们课本上那些顺口溜 SAS,ASA,AAS,HL 本质上也是通过上述基本操作证明的,然而大多数学生却忘了这些基本操作背后的逻辑,本末倒置去适配那些顺口溜。
关注量之间的关系,而不是关注如何取巧,仍以本文的题目说明,B,E,C,F 四点共圆,圆心的轨迹从 ABC 的中心移动到 BCG 的中心,这里设 CG = CB。
更直观的图示如下:
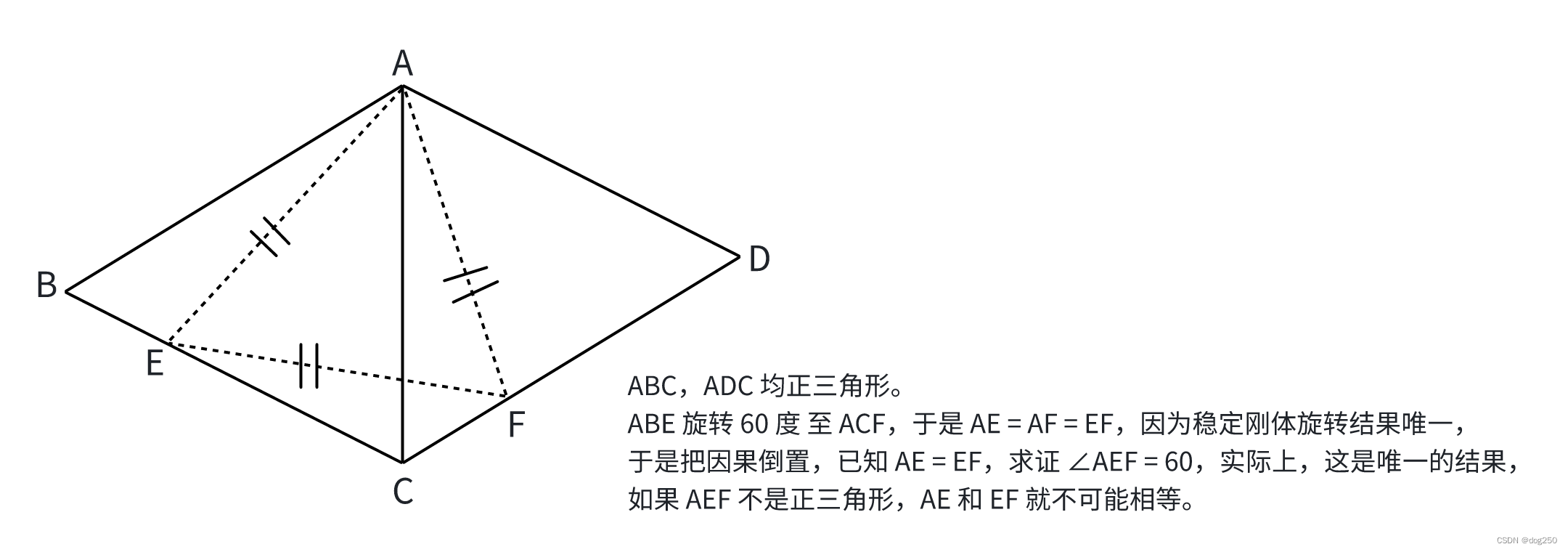
浙江温州皮鞋湿,下雨进水不会胖。
这篇关于一道全等三角形证明题的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!