最长线段（几何证明题）

本文主要是介绍最长线段（几何证明题），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

最长线段（chord.pas/chord.in/chord.out）

（LYOI信息学综合模拟20090321Problem 1）
问题描述
给定两个圆各自的圆心坐标和半径长。过其中一个交点作直线，该直线与圆的另外两个交点分别为A、B。线段AB最长是多少？
输入数据
第一行有三个用空格隔开的整数x1,y1,r1，依次表示第一个圆的圆心坐标和半径；
第二行有三个用空格隔开的整数x2,y2,r2，依次表示第二个圆的圆心坐标和半径；
输入数据保证两圆相交。
输出数据
输出AB的最大长度。你的输出需要保留6位小数。
输入样例
5 4 4
-3 2 5
输出样例
16.492423
数据规模
对于30%的数据，x1=y1；
对于50%的数据，r1=r2；
对于100%的数据，输入数据在integer范围内。
思路
这个题其实我是靠直觉做的，然后它的辅助证明类似于JSQ大佬的方法，我自己造了几组圆然后算了算，发现是当这条线段垂直于两交点连线时最短，然后利用一组相似三角形即可求出解的比值大概是2:1，所以就是圆心距的2倍。

正解思路是用几何证明证明出这个答案是对的。
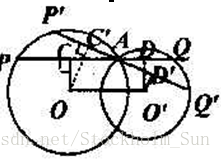
这里写图片描述
求证：经过相交两圆的一个交点的那些直线，被两圆所截得的线段中，平行于连心线的那一条线段最长。
分析：如图，PQ∥OO′，要证明PQ最长，只须证明PQ大于过A点的任意一条不平行于OO′的割线P′Q′，这是证明与圆的弦有关的问题，因此过O、O′分别作PQ、P′Q′的垂线，垂足分别为C、D；C′、D′。由垂径定理知AC= AP、AD= AQ，所以CD= PQ。同理C′D′= P′Q′，又OO′=CD，于是问题转化为证明OO′> C′D′，而OO′D′C′为直角梯形，显然有OO′> C′D′。从而问题可证。

然后放上比较简单的代码。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstdlib>
#include<cmath>
using namespace std;
double x1,x2,y,y2,r1,r2;
int main()
{freopen("chord.in","r",stdin);freopen("chord.out","w",stdout);scanf("%lf%lf%lf",&x1,&y,&r1);scanf("%lf%lf%lf",&x2,&y2,&r2);printf("%.6lf",2*sqrt((x1-x2)*(x1-x2)+(y-y2)*(y-y2)));return 0;
}
/*
5 4 4
-3 2 5
*/