漫步微积分十六——最大最小值问题

本文主要是介绍漫步微积分十六——最大最小值问题，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

微积分最引人注目的应用就是寻找函数的最大或最小值或者需要用到最大和最小值。

日常生活充满了这样的问题，数学家和其他人觉得它们很有趣也非常重要。一个商人旨在使利润最大化和成本最小化。工程师设计的新汽车希望其效率最大化。航空公司飞行员希望减少飞行时间和燃料消耗。在科学中，我们经常发现自然以某种方式在最大化或最小化某一量。例如，一缕光线穿过透镜，总是沿着时间最短的那条路径。挂链最终的形状其重力势能最小。

每当我们使用"最大最小”最多"至少”“最好的”等等这类字眼时，它是一个合理的猜测，某些最大或最小问题只限于某个范围内。如果这个问题可以用变量和函数来表示(并非所有情况都是如此)，那么微积分的方法将帮助我们理解并解决它。

这里许多例子和问题都是用几何的想法来解决，因为最大和最小值在几何中表示特别生动。

我们与一个相当简单有关数的实例开始。

例1：找出两个正数，他们的和为16，乘积尽可能大。

解：如果$x,y$是两个变量，他们的和为16

$$\begin{equation} x+y=16\tag1 \end{equation}$$
那么我们需要找的就是特定的 $x,y$，并最大化他们的乘积
$$\begin{equation} P=xy\tag2 \end{equation}$$
我们的难点在于 $P$依赖于两个变量，而我们的求导只对单个自变量函数有效。等式(1)可以解决这个难点。我们可以用$x$ 来表示 $y$，$y=16-x$，这样 $P$就能只用$x$表示
$$\begin{equation} P=x(16-x)=16x-x^2\tag3 \end{equation}$$
图1我们给出了(3)的大致图像。它的目的是对函数已知事实 $x=0,16,P=0;0<x<16,P>0$给出可视化，最高点根据条件 $dP/dx=0$得出，因为这个条件意味着切线是水平的。对(3)求导
$$\frac{dP}{dx}=16-2x$$
我们令导数等于零
$$\frac{d^2P}{dx^2}=-2$$

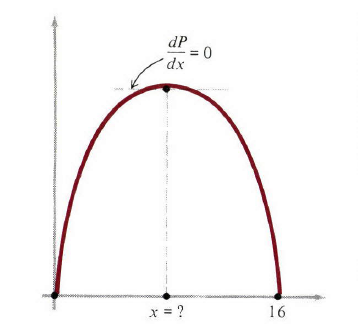
图1

回忆一下，负的二阶导意味着曲线是凸的，因为存在最大值。在给定的限定条件下，如果让 $P$尽可能小，那么将没有解，因为$x,y$必须是正数意味着 $x$必须属于开区间$0<x<16$，从图像中可以看出这部分不存在最小点。

例2：一个矩形花园的面积为450$ft^2$，现在打算围上篱笆防止兔子进入。如果一边已经有一堵墙，那么哪种尺寸可以让篱笆的长度最短？

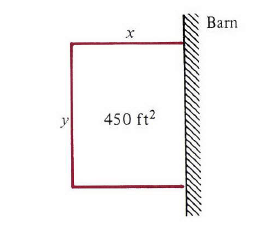
图2

解：我们先画一幅图(图2)，介绍一些符号，来方便我们处理问题。如果$L$表示篱笆的长度，我们需要最小化

$$\begin{equation} L=2x+y\tag4 \end{equation}$$
限制条件为

$$\begin{equation} xy=450\tag5 \end{equation}$$
利用(5)式， $L$可以单独用$x$表示
$$\begin{equation} L=2x+\frac{450}{x}\tag6 \end{equation}$$
快速的画个草图(图3)帮助我们可视化函数并看出它的性质，尤其是它存在最小值，没有最大值(我们只对正的 $x$感兴趣)。下一步就是对(6)求导
$$\frac{dL}{dx}=2-\frac{450}{x^2}$$
然后让它等于零
$$2-\frac{450}{x^2}=0,\quad x^2=225,\quad x=15.$$

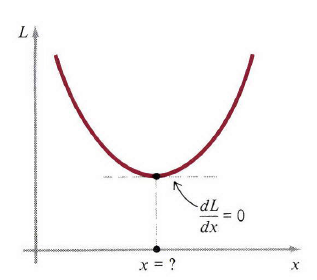
图3

(我们忽略了根$x=-15$)带入(5)，对应的$y$值为$y=30$，所以最短的花园尺寸为$15,30$，或者长是宽的两倍。

例3：找出使矩阵面积最大的尺寸，面积可以用半径为$a$的半圆来描述。

解：我们选取圆$x^2+y^2=a^2$的上半部分(图4左)，那么我们需要最大化

$$\begin{equation} A=2xy\tag7 \end{equation}$$
限制条件为
$$\begin{equation} x^2+y^2=a^2\tag8 \end{equation}$$
由(8)可得 $y=\sqrt{a^2-x^2}=(a^2-x^2)^{1/2}$，(7)就变为
$$\begin{equation} A=2x(a^2-x^2)^{1/2}\tag9 \end{equation}$$

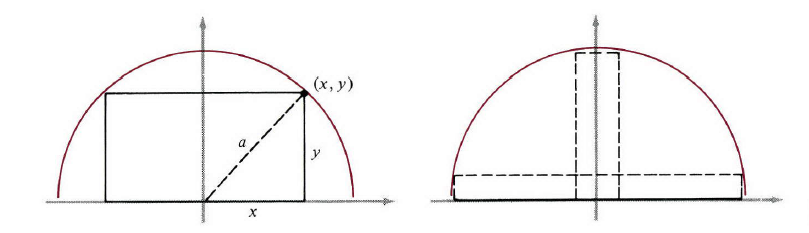
图4

很明显 $x$位于区间$0<x<a$内。图4右中，我们考虑极端的情况：当 $x$趋近0 时，矩形又高又窄，当$x$趋近 $a$时，矩阵又矮又宽，这两种情况下面积都很小，所以在这之间的某个地方存在最大面积。为了找出最大面积，我们从(9)中计算$dA/dx$，令它等于零得：
$$\begin{eqnarray*} &2x\cdot \frac{1}{2}(a^2-x^2)^{-1/2}\cdot (-2x)+2(a^2-x^2)^{1/2}=0,\quad \frac{x^2}{\sqrt{a^2-x^2}}=\sqrt{a^2-x^2}\\ &x^2=a^2-x^2,\quad 2x^2=a^2,\quad x=\frac{a}{\sqrt{2}}=\frac{1}{2}\sqrt{2}a. \end{eqnarray*}$$
因为 $y=\sqrt{a^2-x^2}$，对应的 $y$值为$\frac{1}{2}\sqrt{2}a$，所以最大矩形的尺寸为 $2x=\sqrt{2}a,y=\frac{1}{2}\sqrt{2}a$，这个矩形长是宽的两倍。

如果不考虑具体尺寸，只关心形状的话，还有一个更有效的方法。首先我们注意到(8) 式可以看做$x$ 的隐函数，所以对$x$进行隐式求导得

$$\begin{equation} 2x+2y\frac{dy}{dx}=0\quad or\quad \frac{dy}{dx}=-\frac{x}{y}\tag10 \end{equation}$$
下一步，(7)式求导并利用最大值时 $dA/dx=0$得
$$\begin{equation} 2x\frac{dy}{dx}+2y=0\quad or \quad x\frac{dy}{dx}+y=0.\tag11 \end{equation}$$
将(10)代入(11)得
$$x\left(-\frac{x}{y}\right)+y=0,\quad -x^2+y^2=0,\quad y^2=x^2\quad or\quad y=x.$$
最后的等式给出了最大面积对应的矩形形状。我们也可以说矩阵的高度和宽度之比为
$$\frac{y}{2x}=\frac{x}{2x}=\frac{1}{2}$$
例4：一根长为 $L$的线被切成两部分，一个折成正方形，另一个折成圆。如果要使两部分围成的面积和最大或最小，应该如何切呢？

解：用$x$表示正方形的边长， $r$表示圆的半径，如图5所示，那么面积和为

$$\begin{equation} A=x^2+\pi r^2\tag12 \end{equation}$$
其中 $x$和$r$的关系为
$$\begin{equation} 4x+2\pi r=L\tag13 \end{equation}$$

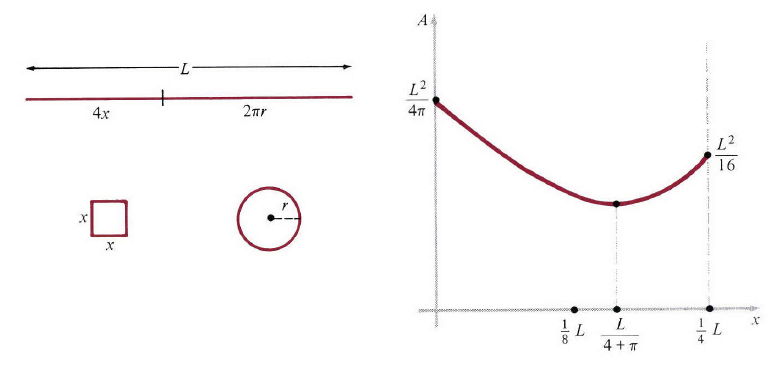
图5

根据(13)式，我们用 $x$表示$r$
$$r=\frac{1}{2\pi}(L-4x)$$
利用此式可以得到只用 $x$表示的$A$
$$\begin{align} A &=x^2+\pi\cdot \frac{1}{4\pi^2}(L-4x)^2\notag\\ &=x^2+\frac{1}{4\pi}(L-4x)^2 \end{align}$$
现在我们注意到，当 $x=0$时，线都用来做圆，当 $x=\frac{1}{4}L$时，都用来做正方形。为了解决问题，我们必须完全理解函数(14)在区间 $0\leq x\leq \frac{1}{4}L$上的行为。在 $x=0,x=\frac{1}{4}L$处的值为 $L^2/4\pi,L^2/16$，第一个更大(因为 $16>4\pi$)。图5表示了出来。因为(14)表明，图像是开口向上( $x^2$系数为正)的抛物线，接下来的工作就是求出最低点的位置。为此，我们对(14)求导
$$\begin{eqnarray*} \frac{dA}{dx} &=&2x+\frac{1}{4\pi}\cdot 2(L-4x)\cdot(-4)\\ &=&2x-\frac{2}{\pi}(L-4x) \end{eqnarray*}$$
令等式为零得
$$x-\frac{1}{\pi}(L-4x)=0,\quad \pi x=L-4x,\quad x=\frac{L}{4+\pi}$$

最高点位于左边的端点处，因此要最大化$A$，必须选择$x=0$,也就说都用来围成一个圆。如果我们坚持两样都需要，那么不存在最大值；因为无论我们用于正方形的长度多么小，我们总能够让它更来使得面积更大。

如果是最小化的话，解为$x=L/(4+\pi)$。因此，正方形的长度为$4x=4L/(4+\pi)$，圆的周长为

$$L-4x=L-\frac{4L}{4+\pi}=\frac{\pi L}{4+\pi}$$
我们还注意到，当圆的周长等于正方形的边长时可以得到最小面积
$$2r=\frac{1}{\pi}(L-4x)=\frac{1}{\pi}\cdot\frac{\pi L}{4+\pi}=\frac{L}{4+\pi}$$

例5：土豆削皮器以单价1.5美元(成本是70美分)出售，那么可以卖出500个。单价每降低一美分，销售量就增加25个。问单价为多少时总利润最高？

解：$x$表示价格降低了多少美分，那么每个产品的利润为$80-x$，销售量为$500+25x$。总利润为

$$P=(80-x)(500+25x)=40000+1500x-25x^2$$
我们令它的导数等于零的
$$\frac{dP}{dx}=1500-50x,\quad 1500-50x=0\quad 50x=1500,\quad x=30$$
最有利的销售价格为1.2美元。

这些例子表明，用于求解最大最小问题的数学方法相当简单。最难的部分如何用简单的形式来建模。这是分析、思考的问题，与计算不一样。我们强调这一点是为了说明，在科学中将微积分作为一种工具的话，那它不太可能有太大的价值，除非学会如何理解问题以及将问题翻译成合适的数学语言。

对于待解决的问题规则并不见得都有效，因为还需要想象力和智力，这是没法教的。然而，以下的一般性建议可能会有帮助。他们并不能保证成功，但没有他们就不太可能有所进展。

求最大最小值的策略

1理解问题$\quad$ 开始先认真的读问题，如果需要可以多读几遍，直到完全理解。然而现实却比较让人难过，那多学生在对问题还不清晰的情况下就看是考虑如何解决。所以花些时间理解问题，让你的努力不至于白费。

2如果涉及几何，那就认真画出图像$\quad$ 例如，如果一个问题是关于一般三角形的，那就不要画直角或等腰三角形误导自己。要认真画图，图像将是得到有效想法的来源，因此要认真对待。

3认真标注图像$\quad$ 确定你理解哪些量是不变的，哪些是变化的。如果方便的话，最好用首字母来表示变量，例如用$A$表示面积(area)，用$V$表示体积(volume)，用$h$表示高度(height)。知道图像中量之间的关系，尤其是涉及到直角和相似三角形。写下他们的等式，提前做好准备。

4如果$Q$是最大或最小化的量，用图像中的量进行表示，尝试用步骤3中的关系得到一个量表示的 Q <script type="math/tex" id="MathJax-Element-12779">Q</script>。在合适的区间内快速画出函数的大致图像，可以在图像上观察一些极端情况并用求导发现具体细节从而得到问题的解。

这篇关于漫步微积分十六——最大最小值问题的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---