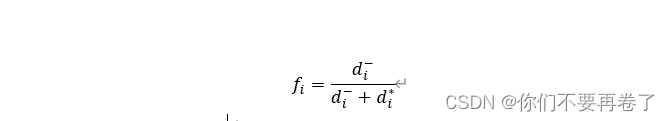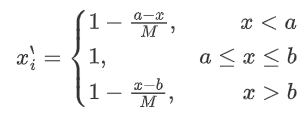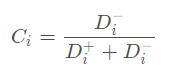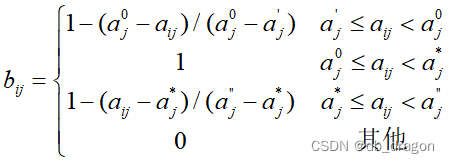topsis专题
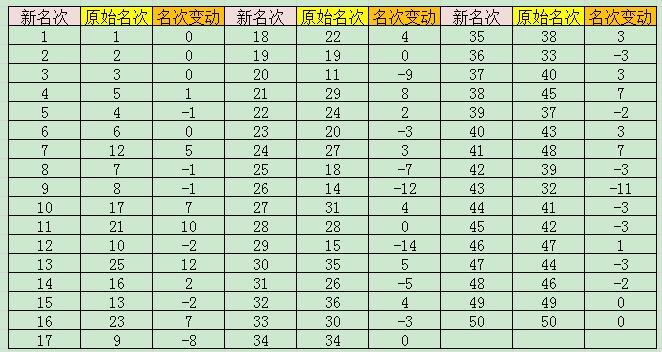
用基于信息熵的topsis方法实现学生成绩的综合排名
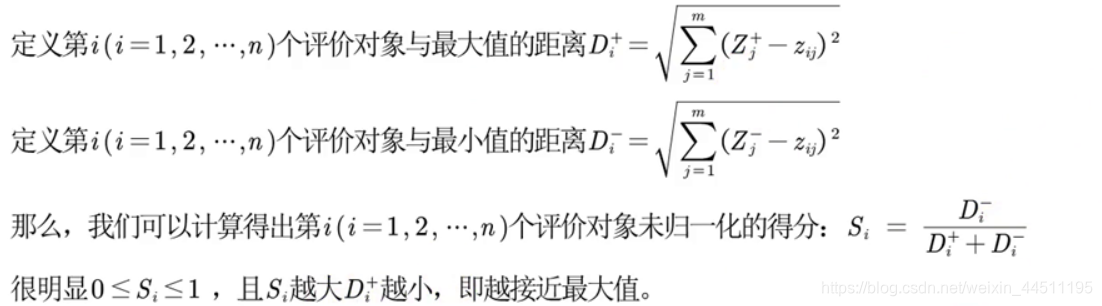
TOPSIS方法排序的基本思路是首先定义决策问题的正理想解(即最好的)和负理想解(即最坏的),然后把实际可行解(样本)和正理想解与负理想解作比较。通过计算实际可行解与正理想解和负理想解的加权欧氏距离,得出实际可行解与正理想解的接近程度,以此作为排序的依据。若某个可行解(样本)最靠近理想解,同时又最远离负理想解,则此解排序最靠前。 通常,当排序时有多个指标需要考虑时,常用“专家打分法”来确定各个指
利用TOPSIS算法进行生长素和施肥量对农作物各指标影响力的分析
文章目录 §1 摘要§2 问题的重述1. 背景介绍2. 问题的产生及进行数学建模的意义 §3 TOPSIS算法1. TOPSIS算法介绍2. TOPSIS算法使用步骤 §4 问题的分析1. 对问题一的分析及解答2. 对问题二的分析及解答3. 对问题三的分析及解答 §5 模型的改进1. 验证2.模型改进 附录问题一代码:问题二代码:问题三代码: §1 摘要 本文旨在分析生
【数学建模】TOPSIS法(优劣解距离法)
TOPSIS法(Technique for Order Preference by Similarity to Ideal Solution,优劣解距离法)是一种多准则决策分析方法,它基于这样一个概念:最理想的方案应该是距离理想解最近而距离负理想解最远的方案。以下是使用TOPSIS法的详细步骤: TOPSIS法的基本步骤 构建决策矩阵: 将所有方案在各个准则下的性能数据
数学建模学习(129):使用Python基于TOPSIS算法的多准则决策分析
案例代码都可做模板,但一定要理解原理和代码的逻辑。 文章目录 1. 引言2. TOPSIS算法原理与步骤2.1 MCDA背景与TOPSIS的适用性2.2 TOPSIS算法的详细步骤解析与数学公式 3. 案例背景与应用场景4. 数据说明与标准化处理4.1 数据4.2 数据标准化步骤与权重选择 5. 代码实现5.1 代码5.2 结果分析 1. 引言 在当今快速发展的信息时
topsis综合评价法
TOPSIS综合评价法(Technique for Order Preference by Similarity to Ideal Solution)是一种多目标决策分析中的有效方法,也被称为优劣解距离法。该方法基于评价对象与理想化目标的接近程度进行排序,从而评估现有对象的相对优劣。以下是TOPSIS综合评价法的详细介绍: 一、定义与简介 定义:TOPSIS综合评价法是一种根据有限个评价对象与理
【数学建模】优劣解距离法Topsis模型(含MATLAB代码)
TOPSIS法,全称 Technique for Order Preference by Similarity to an Ideal Solution,是由C.L.Hwang和K.Yoon于1981年首次提出的 。这是一种多目标决策分析中常用的有效方法,也被称作优劣解距离法 。 TOPSIS法的基本原理是通过检测评价对象与最优解、最劣解的距离来进行排序。如果一个方案距离理想最优解越近,距离最劣解
清风数学建模学习笔记(二)TOPSIS法练习题附代码
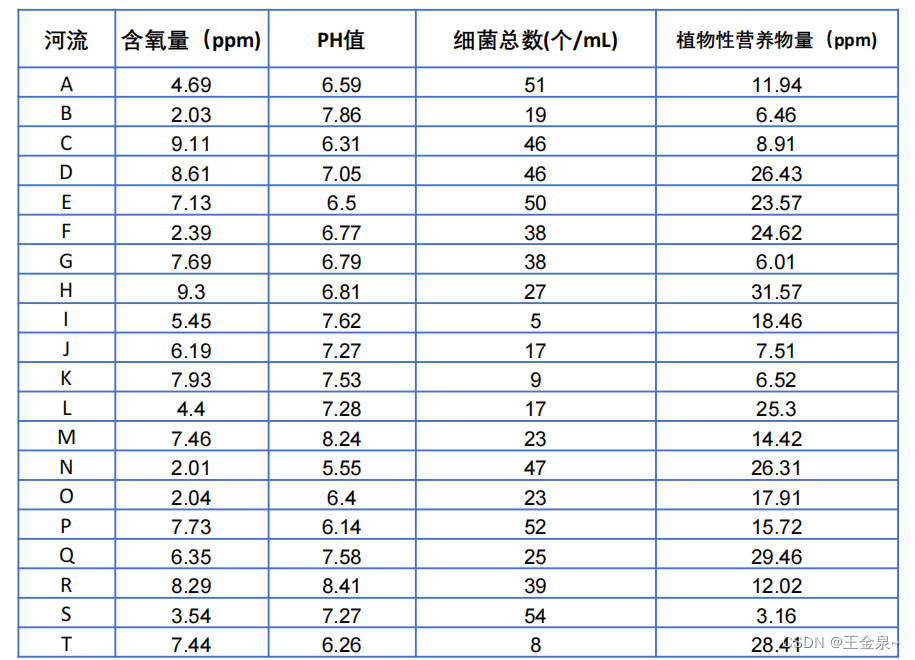
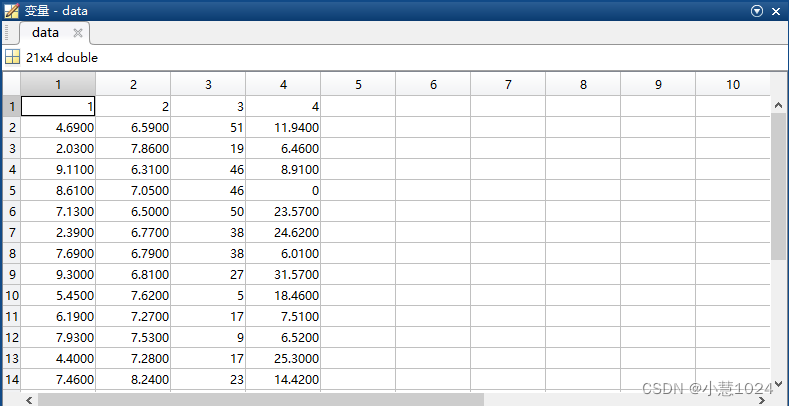
题目:评价下表中20条河流的水质情况。 注:含氧量越高越好;PH值越接近7越好;细菌总数越少越好;植物性营养物量介于10‐20之间最佳,超过20或低于10均不好。 首先TOPSIS方法步骤如下: 1.判断是否需要正向化 2.对正向化后的矩阵进行标准化 3.计算与最大值的距离和最小值的距离,并算出得分 一、判断是否需要正向化 由表格可知,
优劣解距离法(TOPSIS)
方法步骤 1.将原始矩阵正向化 最常见的四种指标: 原始矩阵正向化的本质其实是要将所有的指标类型统一转化为极大型指标。 极小型指标 -> 极大型指标 公式:max - x 如果所有元素均为正数,那么也可以使用1/x。 中间型指标 -> 极大型指标 中间型指标:指标值既不要太大,也不要太小,去某特定值最好(如水质量评估PH值) 公式: 区间型指标 -> 极大型指标 区间型指标: 指标值落在某个区
【评价类模型】Topsis法(优劣解距离法)
【评价类模型】Topsis法(优劣解距离法) 学习前言 Topsis法解决问题三步曲: 第一步:将原始矩阵正向化 最常见的四种指标: 极小型指标转换为极大型指标: 中间型指标转换为极大型指标: 区间型指标转换为极大型指标: 第二步:正向化后
TOPSIS 优劣解距离法 学习笔记
目录 一.TOPSIS方法(优劣解距离法) 二.步骤 1.指标正向化 (1)极小型指标的正向化 (2)中间型指标的正向化 (3)区间型指标的正向化 2.计算得分 三.拓展-增加权重 (1)判断矩阵 (2)熵权法 步骤: 局限: 一.TOPSIS方法(优劣解距离法) 逼近理想解排序法。 针对已有数据的评价类问题,将各个指标合理得分,方便最终比较得出最佳方案。
02【评价类】模型——TOPSIS法(理想解法、优劣解距离法)
02【评价类】模型——TOPSIS法(理想解法、优劣解距离法) 目录 02【评价类】模型——TOPSIS法(理想解法、优劣解距离法) 一、引述 二、TOPSIS法的应用 2.1 决策矩阵正向化处理 2.1.1 效益型指标(极大型指标) 2.1.2 成本型指标(极小型指标) 2.1.3 区间型指标 2.1.4 中间型指标 2.1.5 问题解决 2.2 正向化矩阵规
【数学建模】清风视频笔记2、TOPSIS法(优劣解距离法)
TOPSIS法(优劣解距离法) 例子 小明和同学第一学期高数成绩 姓名成绩排名修正后的排名评分小明89233/10=0.3小王60 10411/10=0.1小张74322/10=0.2清风99 90144/10=0.4 只要排名不变评分就不会变 最高成绩max:99 最低成绩min:60 姓名成绩未归一化的评分归一化评分小明89(89-60)/(99-60)=0.740.74/2.1
综合评价算法 | Matlab实现基于随机TOPSIS法的综合评价算法
文章目录 效果一览文章概述研究内容源码设计参考资料 效果一览 文章概述 综合评价算法 | Matlab实现基于随机TOPSIS法的综合评价算法 研究内容 随机TOPSIS 法是一种常用的组内综合评价方法,能充分利用原始数据的信息,其结果能精确地反映各评价方案之间的差距。基本过程为基于归一化后的原始数据矩阵,随机确定权重,采用余弦法找出有限方案中的最优方案
【建模算法】TOPSIS法(Python实现)
【建模算法】TOPSIS法(Python实现) Topsis法,全称为Technique for Order Preference by Similarity to an Ideal Solution,中文常翻译为“优劣解距离法”或“逼近理想解排序法”,该方法是一种通过比较样本值与理想值的距离实现综合评价的方法。能够根据现有的数据,对个体进行评价排序。TOPSIS算法是直接用来评价的,它也可以和
基于matlab的TOPSIS(优劣距离法)综合评价模型
C.L.Hwang 和 K.Yoon 于1981年首次提出 TOPSIS ,可翻译为逼近理想解排序法,国内常简称为优劣解距离法。 TOPSIS 法是一种常用的综合评价方法,能充分利用原始数据的 信息,其结果能精确地反映各评价方案之间的差距。 基本过程为先将原始数据矩阵统一指标类型(一般正向化处理) 得到正向化的矩阵,再对正向化的矩阵进行标准化处理以消除各指 标量纲的影响,并找到有限方案中的最
MATLAB优劣解距离法(topsis)综合评价+代码
优劣解距离法 TOPSIS是通过逼近理想解的程度来评估各个样本的优劣等级 收集与整理 假设有n个待评价样本,p项评价指标,形成原始指标数据矩阵: 预处理数据 使指标具有同趋势性。评价指标中有正向指标和负向指标之分,一般把负向指标转化为正向指标,转化的方法可采用倒数法(即1/X),多适用于绝对数指标;差值法(即1-X),多适用于相对数指标。转化后的数据矩阵仍记为X。数据无量纲化.。将原始
优劣解距离法(topsis)综合评价+代码
优劣解距离法 TOPSIS是通过逼近理想解的程度来评估各个样本的优劣等级 收集与整理 假设有n个待评价样本,p项评价指标,形成原始指标数据矩阵: 预处理数据 使指标具有同趋势性。评价指标中有正向指标和负向指标之分,一般把负向指标转化为正向指标,转化的方法可采用倒数法(即1/X),多适用于绝对数指标;差值法(即1-X),多适用于相对数指标。转化后的数据矩阵仍记为X。数据无量纲化.。将原始数据归一
用MATLAB实现topsis评价法
最近将topsis评价方法用matlab实现了,就此分享一下具体操作方法,以供大家参考纠正。 1 将topsis的评价流程及函数方程列出 1.1 对各评价对象的参数矩阵进行同向化处理。 一般选择正向化处理,下面列举一些网络上其他博主的公式,以供参考使用。 1.1.1 极大型指标正向化 极大型指标所指意思为,这个指标越大越好,例如(升学率,毕业率等) X:各极大型属性指标的参数;
一个简单实用的评价模型——TOPSIS理想解法
Hello!大家好,今天给大家介绍的是一个非常简单实用又好理解的评价模型——TOPSIS理想解法。本次案例的理论知识和数据均来自于《数学建模与数学实验》这本书,如果有想看该书的小伙伴,可在公众号中回复“《数学建模与数学实验》”(注意要打“《》”),即可获得该书的电子版,废话不多说,咱们直接进入正题。 TOPSIS理想解法 TOPSIS原理基本原理算法步骤 Python代码实现获得代码
数学建模学习(4):TOPSIS 综合评价模型及编程实战
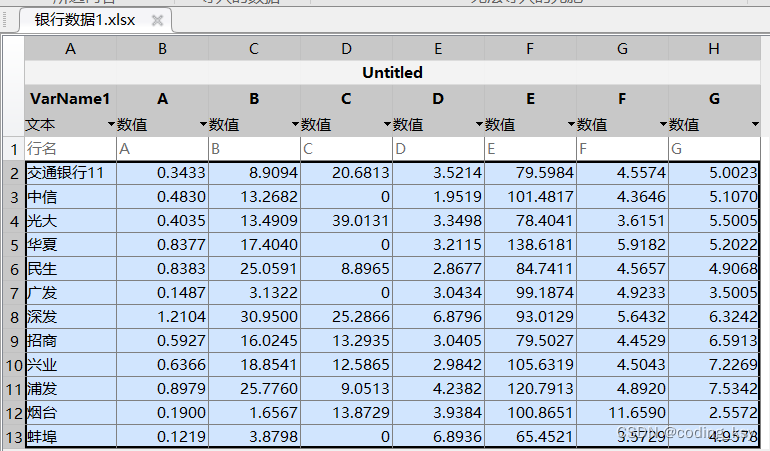
一、数据总览 需求:我们需要对各个银行进行评价,A-G为银行的各个指标,下面是银行的数据: 二、代码逐行实现 清空代码和变量的指令 clear;clc; 层次分析法 每一行代表一个对象的指标评分 p = [8,7,6,8;7,8,8,7];%每一行代表一个对象的指标评分 A为自己构造的输入判别矩阵 %A为自己构造的输入判别矩阵A=[1,3,1,1/3;
数学建模(二)、TOPSIS法(优劣解距离法)
TOPSIS 法(优劣解距离法) 1、什么是 TOPSIS 法(优劣解距离法)?2、解法步骤统一指标类型标准化处理(消除不同指标量纲的影响)通过标准化矩阵计算评分 1、什么是TOPSIS法(优劣解距离法)? TOPSIS 法是一种理想目标相似性的顺序选优技术,在多目标决策分析中是一种非常有效的方法。它通过归一化后的数据规范化矩阵,找出多个目标中最优目标和最劣目标 (分别用理想
TOPSIS优劣解距离法(自用)1
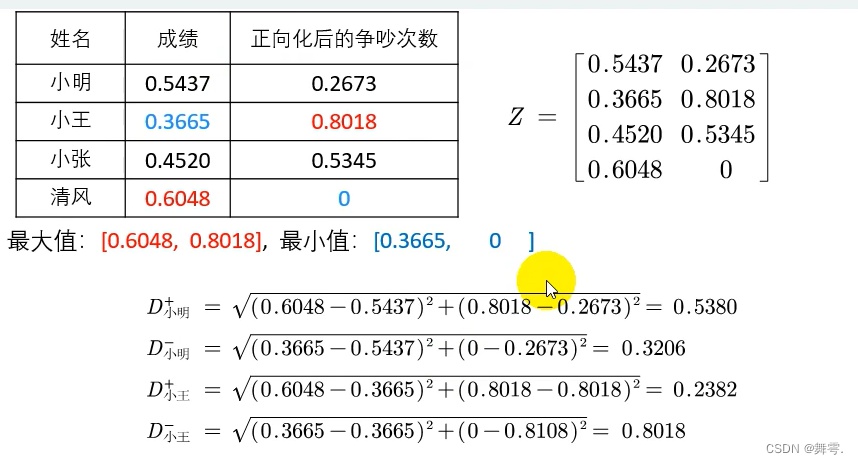
对于上一节,我们讲了AHP方法。但是层次分析法有一定的缺陷 引例 在这里我们看到,排名是越小越好。但是,我们是想打分,打分的话就是分数越大越好,所以我们为了合理地打分,就要对这个排名进行转化,怎么转化? 我们将原来的排名越小越好修正为越大越好。然后给出评分就是上图所示。 但是,我们的上面这个方法有不合理之处。比如,如果小王和清风考得是另一个成绩,但是他们的名次就还是没有发生改变,这时候,
评价模型:TOPSIS法(理想解法)
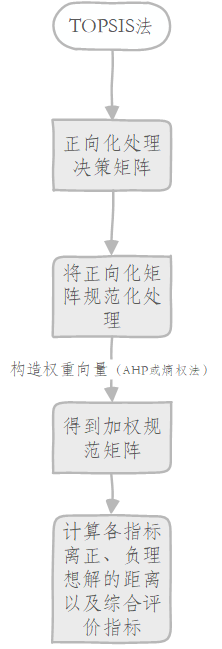
写在前面: 博主本人大学期间参加数学建模竞赛十多余次,获奖等级均在二等奖以上。为了让更多学生在数学建模这条路上少走弯路,故将数学建模常用数学模型算法汇聚于此专栏,希望能够对要参加数学建模比赛的同学们有所帮助。 目录 1.算法介绍 2.算法步骤 (1)用向量规范化的方法求得规范决策矩阵 (2)构造加权规范阵 (3)确定正理想解和负理想解 (4)计算各方案到正理想解与负理想解的距