【数学建模】清风视频笔记2、TOPSIS法（优劣解距离法）

本文主要是介绍【数学建模】清风视频笔记2、TOPSIS法（优劣解距离法），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

TOPSIS法（优劣解距离法）

例子

小明和同学第一学期高数成绩

姓名	成绩	排名	修正后的排名	评分
小明	89	2	3	3/10=0.3
小王	60 10	4	1	1/10=0.1
小张	74	3	2	2/10=0.2
清风	99 90	1	4	4/10=0.4

只要排名不变评分就不会变

最高成绩max：99

最低成绩min：60

姓名	成绩	未归一化的评分	归一化评分
小明	89	（89-60）/（99-60）=0.74	0.74/2.1=0.35
小王	60	（60-60）/（99-60）=0	0/2.1=0
小张	74	（74-60）/（99-60）=0.36	0.36/2.1=0.17
清风	99	（99-60）/（99-60）=1	1/2.1=0.48

$$\frac{x-min}{max-min}$$
原因：

1、比较对象一般远大于两个

2、比较的指标往往不只是一方面的

3、很多指标不存在理论上的最大值和最小值

姓名	成绩	争吵次数
小明	89	2
小王	60	0
小张	74	1
清风	99	3

成绩是越高越好，这样的指标称为极大型指标（效益型指标）

争吵是越少越好，这样的指标称为极小型指标（成本型指标）

**指标正向化：**把所有的指标转化为极大型。$max-x$

为了消去不同指标量纲的影响，需要对已经正向化的矩阵进行标准化处理
$$z_{ij}=\frac{x_{ij}}{\sqrt{{\sum }_{i=1}^n{x}_{ij}^2}}$$
当只有一个指标的时候可看作：
$$\frac{x与最小值的距离}{x与最大值的距离+x与最小值的距离}$$
如何计算得分

姓名	正向化后的成绩	正向化后的争吵次数
小明	0.5437	0.2673
小王	0.3665	0.8018
小张	0.4520	0.5345
清风	0.6048	0

$最大值:[0.6048,0.8018],最小值：[0.3665,0]$

$D_{小明}^{+}=\sqrt{(6048-0.5437{)}^2+(0.8018-0.2673{)}^2}=0.5380$

$D_{小明}^{-}=\sqrt{(0.3665-0.5437{)}^2+(0-0.2673{)}^2}=0.3206$

$D_{小王}^{+}=\sqrt{(0.6048-0.3665{)}^2+(0.8018-0.8018{)}^2}=0.2382$

$D_{小王}^{-}=\sqrt{(0.3665-0.3665{)}^2+(0.8018-0{)}^2}=0.8018$

总结

步骤：

1、将所有数据极大化

• 极小型：$max-x$
• 中间型： M = m a x { ∣ x i − x b e s t ∣ } , x i ‘ = 1 − ∣ x i − x b e s t ∣ M M=max\left\{|x_i-x_{best}|\right\},x_i^`=1-\frac{|x_{i}-x_{best}|}{M} M=max{∣xi​−xbest​∣},xi‘​=1−M∣xi​−xbest​∣​
• 区间型： M = m a x { a − m i n { x i } , m a x { x i } − b } M=max\left\{a-min\left\{x_i\right\},max\left\{x_i\right\}-b\right\} M=max{a−min{xi​},max{xi​}−b}

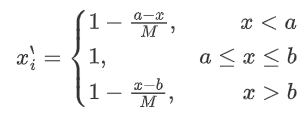
2、正向化矩阵标准化

3、计算得分并归一化

这篇关于【数学建模】清风视频笔记2、TOPSIS法（优劣解距离法）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---