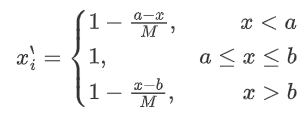清风专题
《他强由他强,清风拂山岗;他横由他横,明月照大江》之四
JVM垃圾回收 1.JVM中判断对象存活的方法 引用计数法 每个对象都有一个与之关联的引用计数器,每当有一个地方引用它时,计数器值就加1;当引用失效时,计数器值就减1。 优点:高效、简单 缺点:无法解决循环引用问题可达性分析算法 目前主流的商用程序语言(包括Java)主要采用的算法,它通过一系列的"GC Roots"作为起始点,从这些节点开始向下搜索,搜索所走过的路径称为引用链(Referen
《他强由他强,清风拂山岗;他横由他横,明月照大江》之三
常见的设计模式 1.策略模式 使用场景 通俗来说,策略模式就像是让你有一个策略的工具箱,在不同的情况下选择最合适的策略来解决问题。 使用场景通常包括以下一些: 多重条件判断语句: 当一个操作包含大量的条件判断语句,并且这些分支具有不同的行为时,可以使用策略模式来避免复杂的条件判断逻辑,让代码更加清晰、易于维护。 同一操作有多种实现: 当你有一个操作,它可以有多种不同的实现方式(算法),而且你希
雨云:不只是一阵清风,更是一场暴雨的力量
引言 在网络时代,服务器是任何在线业务的核心。无论你是运营一家小型博客还是承载着数百万用户的大型电商平台,都需要一个稳定、高效的服务器来支持你的业务。然而,在众多服务器提供商中,有一家备受推崇,那就是雨云。 为什么选择雨云? 1. 可靠性与稳定性 在选择服务器时,可靠性和稳定性是至关重要的因素。你不希望你的网站因为服务器故障而宕机,导致用户流失和业务损失。而雨云以其
【车机福音】清风DJ无广告免费听纯车机版 超高音质1.0.5 (手机版本也有了)
记得收藏点赞,小手动一动 清风DJ,是由知名品牌DJ网站清风DJ音乐网开发的一款强大多功能的DJ音乐播放器 每天发布最新酒吧夜店潮歌,同步全球醉新DJ歌曲。提供专业DJ精心制作的DJ音乐,车载DJ精品,高清音质在线试听,高音质mp3下载,全方位满足DJ工作者及音乐爱好者的需求。 音乐类型有超劲爆DJ串烧、酒吧慢摇、中文DJ舞曲、英文DJ舞曲、DJ慢歌连版、DJ时尚节奏、DJRemix、Mixes
【其他】清风眼中的《妙手仁心》
我是清风,一个以医生为正职,平时喜欢写点文字的男人。人家喜欢把我称为作家,可是我觉得我还配不上这个称呼。因为我所记录的只是一些身边的人和事,所抒发的也只是一些个人的情感,这与“作家”二字相去甚远。有人也许会问我,作为一个医生,而且是工作负荷最重的A&E的高级医生,平时工作压力已经很大了,为什么还会想到出来写一些东西?的确,A&E可以说是医院里随时候命的一个部门,而且我也是真真切切地热爱这个职业
清风数学建模学习笔记(二)TOPSIS法练习题附代码
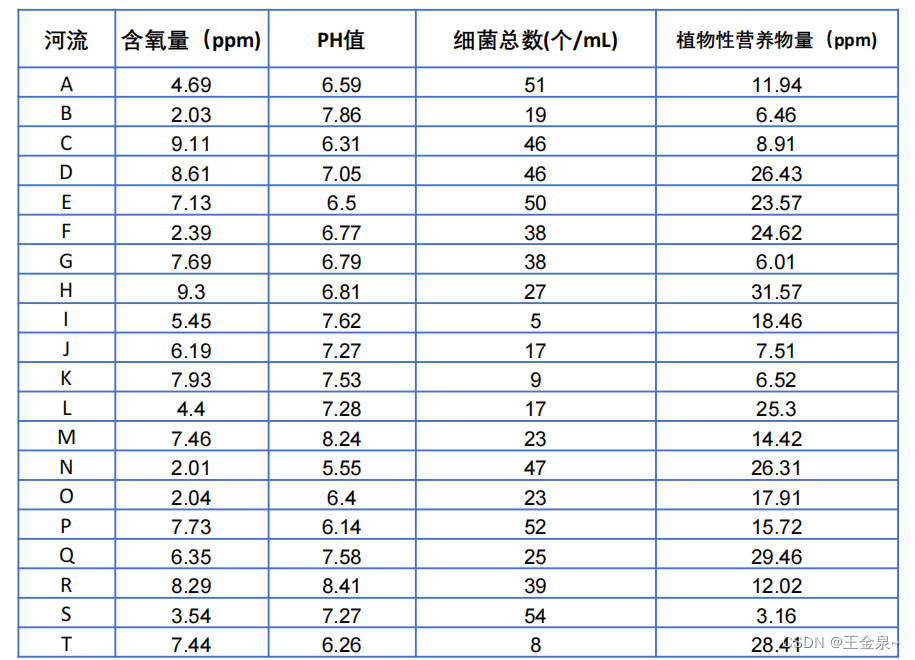
题目:评价下表中20条河流的水质情况。 注:含氧量越高越好;PH值越接近7越好;细菌总数越少越好;植物性营养物量介于10‐20之间最佳,超过20或低于10均不好。 首先TOPSIS方法步骤如下: 1.判断是否需要正向化 2.对正向化后的矩阵进行标准化 3.计算与最大值的距离和最小值的距离,并算出得分 一、判断是否需要正向化 由表格可知,
清风数学建模——模型学习层次分析法
目录 第一讲:层次分析法 step1:为了解决评价类问题,首先想到三个问题: step2:查询资料后选择了以下五个指标: step3:权重表格 step4:层次分析法思想——评价准则的权重计算 4.1 判断矩阵 4.2 一致性检验 4.3 判断矩阵求权重 step5:层次分析法思想——不同方案的权重计算 5.1 判断矩阵 5.2 一致性检验 5.3 判断矩阵求权重
清风带你学-H5+CSS3(六)使用less维护rem布局项目
M-web 掌握less的安装和编译 掌握less的基本语法 掌握在项目中使用less 掌握rem适配的原理 掌握rem+媒体查询适配 掌握rem+flexible适配 课程内容 less 什么是less 作为一门标记性语言,CSS 的语法相对简单,对使用者的要求较低,但同时也带来一些问题:CSS需要书写大量看似没有逻辑的代码,不方便维护及扩展,不利于复用,尤其对于非前端开
清风带你学-H5+CSS3(五)移动端滑动,手势,布局
M-web 了解touch事件的使用 独立完成jdM的轮播图 掌握区域滚动插件使用 了解手势事件的原理 安装less运行环境nodeJS touch事件 触摸事件 事件说明touchstart当手指触碰屏幕时候触发该事件touchmove当手指在屏幕上滑动时候触发该事件touchend当手指离开屏幕时触发该事件touchcancel当系统停止跟踪(被迫终止)触摸时候会触发。
清风数学建模笔记-时间序列分析
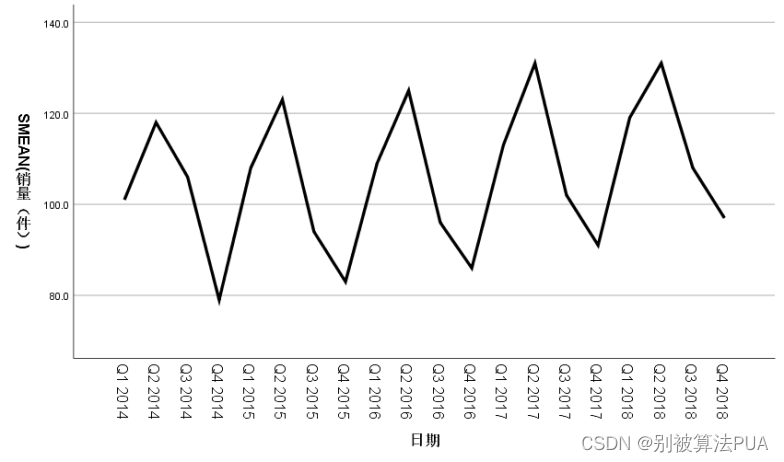
内容:时间预测分析 一.时间序列 1.时点时间序列 2.时期时间序列:可相加 二.时间趋势分解 1.季节趋势 拓展:百度指数: 2.循环变动趋势(和季节很像但是是以年为单位) 3.不规则变动趋势(像扰动项) 4.长期变动趋势 三.叠加模型和乘积模型 四.SPSS处理时间序列分解 1.处理时间序列中的缺失值: 2.定义时期和时间: 3.进行
清风数学建模-数学规划模型
内容:数学规划模型(cab aeqbeq lbub) 一.题型类型 1.线性规划linprog 2.非线性规划 fmincon 3.整数规划 intlinprog 4.(0-1规划)(特殊的线性整数规划)intlinprog 5.多目标规划 linprog 标准化加权 6.最小的最大值fminimax 二.实现步骤 1.看懂题目,列出式子(这时最难的,要多各种模型都了解) 2.
清风数学建模笔记-多分类-fisher线性判别分析
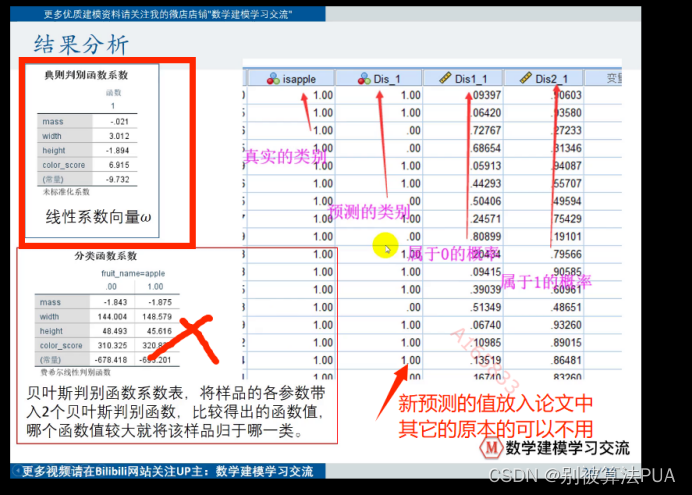
内容:Fisher线性判别分析 一.介绍: 1.给定的训练姐,设法投影到一维的直线上,使得同类样例的投影点尽可能接近和密集,异类投影点尽可能远离。 2.如何同类尽可能接近:方差越小 3.如何异类尽可能远离:计算距离大 二.SPSS进行线性判别分析 1.分析-分类-判别式 分析结果:
清风数学建模学习笔记--灰色关联分析
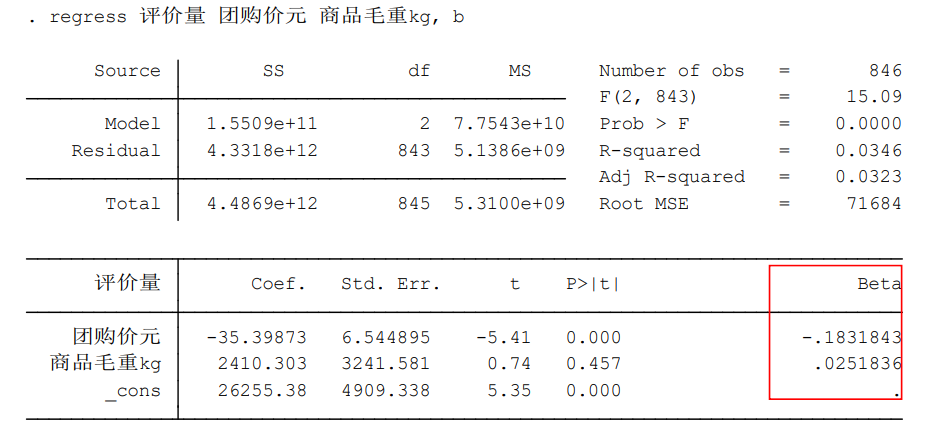
一:内容:灰色关联分析 介绍:可以分析多个因素之间,哪一个对y的影响大,哪一个对y的影响小。之前学过回归分析中的标准化回归也可以分析,岭回归,lasso回归等都可以分析,那为什么要使用灰色关联分析呢? 因为以下原因 1.要求有大数据,数据少就难以找出统计规律。 2.某些数据要求样本服从某个概率分布 3. 二.基本思想: 三.应用 1. 用于系统分析 画统计图 -确定
【数学建模】清风视频笔记3、插值算法
插值算法 “模拟产生”一些新的但又比较靠谱的值来满足需求,针对数据极少情况 一维插值问题 插值多项式: P ( x ) = a 0 + a 1 x + ⋯ + a n x n P(x)=a_0+a_1x+\dots+a_nx^n P(x)=a0+a1x+⋯+anxn 若 P ( x ) P(x) P(x)为分段多项式,就称分段插值 若 P ( x ) P(x) P(x)为三角函数,
【数学建模】清风视频笔记2、TOPSIS法(优劣解距离法)
TOPSIS法(优劣解距离法) 例子 小明和同学第一学期高数成绩 姓名成绩排名修正后的排名评分小明89233/10=0.3小王60 10411/10=0.1小张74322/10=0.2清风99 90144/10=0.4 只要排名不变评分就不会变 最高成绩max:99 最低成绩min:60 姓名成绩未归一化的评分归一化评分小明89(89-60)/(99-60)=0.740.74/2.1
【数学建模】清风视频笔记1、层次分析法
层次分析法 主要用于解决评价类问题. 例子: 小明最关心大学里的四个方面(学习氛围-0.4,就业前景-0.3,男女比例-0.2,校园景色-0.1)括号里面的数值表示小明认为的重要性程度(权重,其和为1). 小明的权重表格 指标权重华科武大学习氛围0.40.70.3就业前景0.30.50.5男女比例0.20.30.7校园景色0.10.250.75 最终华科:0.515;武大:0.485
清风数学建模课笔记-多元回归分析
回归分析 概念 回归分析:研究X和Y的相关性分析 相关性不是因果性 统计数据可以说明:游泳死亡人数越高,雪糕卖的越多。(两者呈显著正相关) 但是不能说 吃雪糕会增加游泳死亡风险 背后的原因应该是天气热 所以相关性不是因果性 在大部分情况下都不能直接说是因果性 Y是因变量 是我们研究的核心变量 -因为别人的改变而改变的变量 连续性指数变量 -GDP -线性回归 0-1型变量 -对错 定序变
【清风】程序流程图是程序的图纸,是程序的灵魂
我相信有不少刚入这一行的开发童鞋,在面对一个需求时,通常没有多加思考,撸起袖子就直接开干。看似大神级别的一顿操作猛如虎,一看代码惨不忍睹。究其根源,是因为缺少分析与设计,导致在开发过程中逻辑不清,头脑混乱,开发出的代码质量堪忧,BUG层出不穷。 万丈高楼平地起,这离不开工程师精心设计的图纸。写代码,也是这样一个道理。 我做了多年开发,每次写关键业务时我都会梳理清思路,画好流程图,由于工作效率提
【数学建模】清风国赛论文技巧
数学建模国赛论文技巧 代码降重表格格式:综合设计 公式上浮附录代码行内公式增加行间距正确转换下一页网页数据导入到excel表格图片数据转换为excel 特等附录物理示意图论文中插入数学公式绘制流程图和思维导图 代码降重 1.代码的每句话加注释 2.更改变量名称 3.模型优缺点需要自己总结,修改 4.汉字加入到公式中(数据加入到了图片) 5.增加空格,或者字符缩小字号,更改字
二、数学建模优劣分析法(TOPSIS法)【清风数学建模个人笔记】
目录 层次分析法的局限 TOPSIS法主要思想 引入 统一指标类型 标准化处理 如何计算得分 只有一个指标 多个指标 计算得分 TOPSIS法步骤 第一步:将原是矩阵正向化 极小型->极大型 中间型->极大型 区间型->极大型 第二步:正向化矩阵标准化 第三步:计算得分并归一化 带权重的TOPSIS法 Topsis代码详解 主函数 自定义函数Positi
主成分分析(清风建模学习笔记)
简介: 本讲将介绍主成分分析 (Principal Component Analysis,PCA) ,主成分分析是一种降维算法,它能将多个指标转换为少数几个主成分,这些主成分是原始变量的线性组合,且彼此之间互不相关,其能反映出原始数据的大部分信息。一般来说,当研究的问题涉及到多变量且变量之间存在很强的相关性时,我们可考虑使用主成分分析的方法来对数据进行简化。 数据降维的作用: