清风数学建模——模型学习层次分析法

目录

第一讲：层次分析法

step1：为了解决评价类问题，首先想到三个问题：

step2：查询资料后选择了以下五个指标：

step3：权重表格

step4：层次分析法思想——评价准则的权重计算

4.1 判断矩阵

4.2 一致性检验

 4.3 判断矩阵求权重

 step5：层次分析法思想——不同方案的权重计算

5.1 判断矩阵

5.2 一致性检验

5.3 判断矩阵求权重

 step6：计算各方案的得分

第二讲：层次分析法代码

step1：输入判断矩阵

step2：判断是否一致

1.一致性检验的步骤

2.求最大特征值

3.求矩阵的n

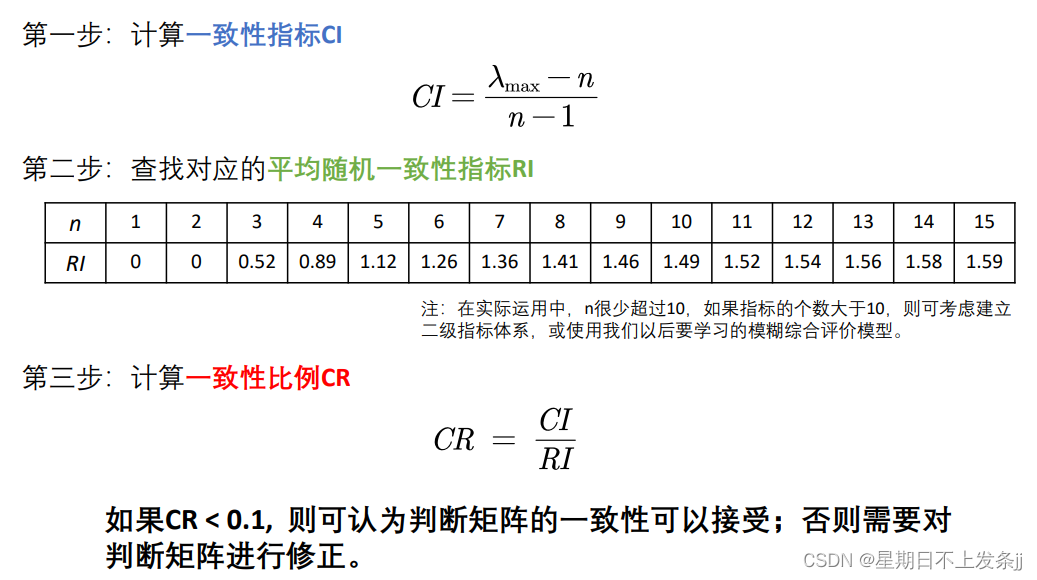
3.计算一致性指标CI

4.查找对应的平均随机一致性指标RI

5.计算一致性比例CR

step3：计算权重

1.算术平均法求权重

2.几何平均值法求权重

3.特征值法求权重

step4：把权重复制到excel表格中去

第三讲：层次分析法作业

---

非原创，看清风数学建模视频课做的笔记，建议去B站观看清风数学建模的课程或者购买正课~

第一讲：层次分析法

step1：为了解决评价类问题，首先想到三个问题：

1. 评价目标？——选择最佳旅游景点
2. 为了达到目标有几种可选择的方案？——有A、B、C三个旅游景点
3. 评价的准则或指标是什么？——需要我们查阅相关资料，优先选择知网、万方、百度学术、谷歌学术等平台搜索相关的文献

step2：查询资料后选择了以下五个指标：

• 景点景色
• 旅游花费
• 居住环境
• 饮食情况
• 交通便利程度

step3：权重表格

	指标权重	A	B	C
景色
花费
居住
饮食
交通

 一次性考虑这五个指标之间的关系，往往考虑不周。

两个两个指标进行比较，最终根据两两比较的结果来推算出权重。

step4：层次分析法思想——评价准则的权重计算

4.1 判断矩阵

标度	含义
1	同样重要
3	稍微重要
5	明显重要
7	强烈重要
9	极端重要
2，4，6，8	上述两相邻判断的中值
倒数	如果花费比景色标度为2，那么景色比花费标度为1/2

	景色	花费	居住	饮食	交通
景色	1	1/2	4	3	3
花费	2	1	7	5	5
居住	1/4	1/7	1	1/2	1/3
饮食	1/3	1/5	2	1	1
交通	1/3	1/5	3	1	1

表格中数值的含义：我认为花费比景色略微重要（介于同等重要1和稍微重要3之间）；我认为景色比居住要重要一点（介于稍微重要3和明显重要5之间）

总结: 上面这个表是一个5 x 5的方阵，我们记为A，对应的元素为aii这个方阵有如下特点
(1) aij表示的意义是，与指标j相比，i的重要程度
(2)当i=j时，两个指标相同，因此同等重要记为1，这就解释了主对角线元素为1。                        (3) aij > 0且满足aij x aji = 1 (我们称满足这一条件的矩阵为正互反矩阵)
实际上，上面这个矩阵就是层次分析法中的判断矩阵。

4.2 一致性检验

一致矩阵
若矩阵中每个元素aij > 0且满足aij*aji = 1 ，则我们称该矩阵为正互反矩阵。                                 在层次分析法中，我们构造的判断矩阵均是正互反矩阵；若正互反矩阵满足aij x ajk = aik， 则我们称其为一致矩阵。【注意，上述矩阵不是一致矩阵，需要进行一致性检验】
注意: 在使用判断矩阵求权重之前，必须对其进行一致性检验。

一致性检验的原理：（原理简略，具体步骤请去看清风数学建模的视频课）

 

 

这里有三种情况：1.判断矩阵是一致矩阵，也就是aij*ajk=aik，那么不需要进行一致性检验，可对该判断矩阵进行求权重；2.判断矩阵不是一致矩阵，但是经过检验认为该判断矩阵的一致性可以接受，则可对该判断矩阵进行求权重；3.判断矩阵不是一致矩阵，并且一致性也不能接受，那么需要对判断矩阵进行修正，比如“景色比居住重要一点”4改为“景色比居住强烈重要”7（打个比方，并不是评价准则的判断矩阵不一致）。

一致性检验的思想大概就是检验：A>B B>C能否推导出A>C

 4.3 判断矩阵求权重

• 算术平均法
• 几何平均法
• 特征值法

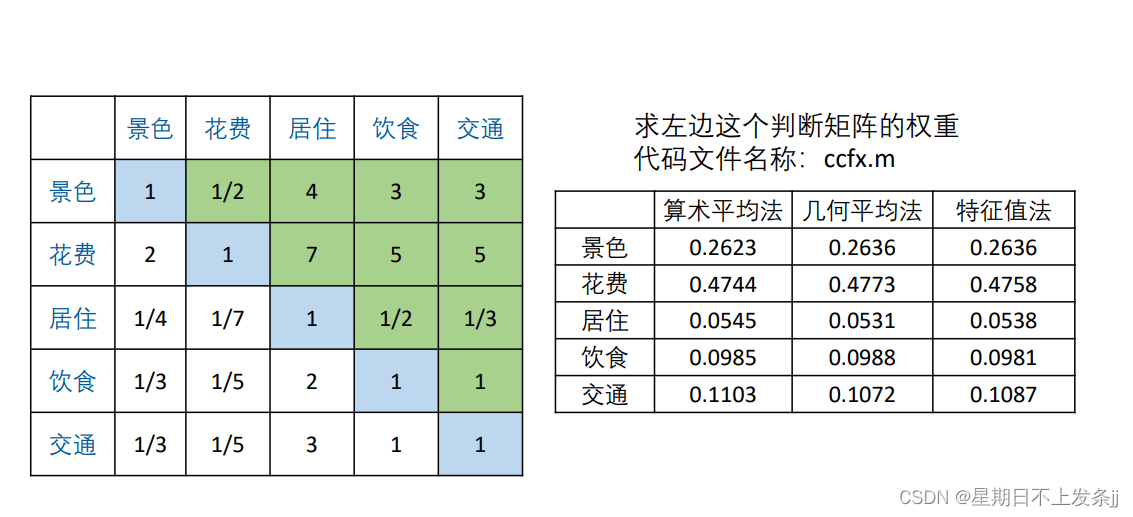
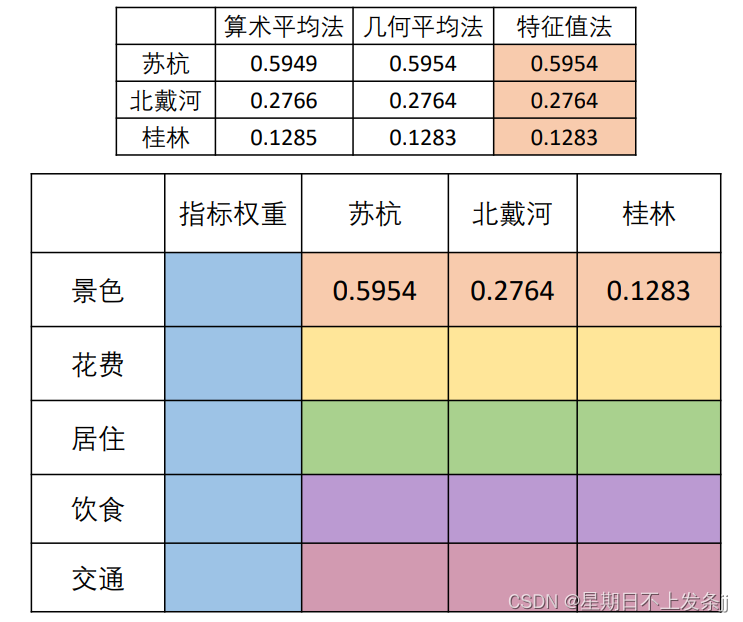
 利用特征值法求出来的权重

 step5：层次分析法思想——不同方案的权重计算

5.1 判断矩阵

 

 

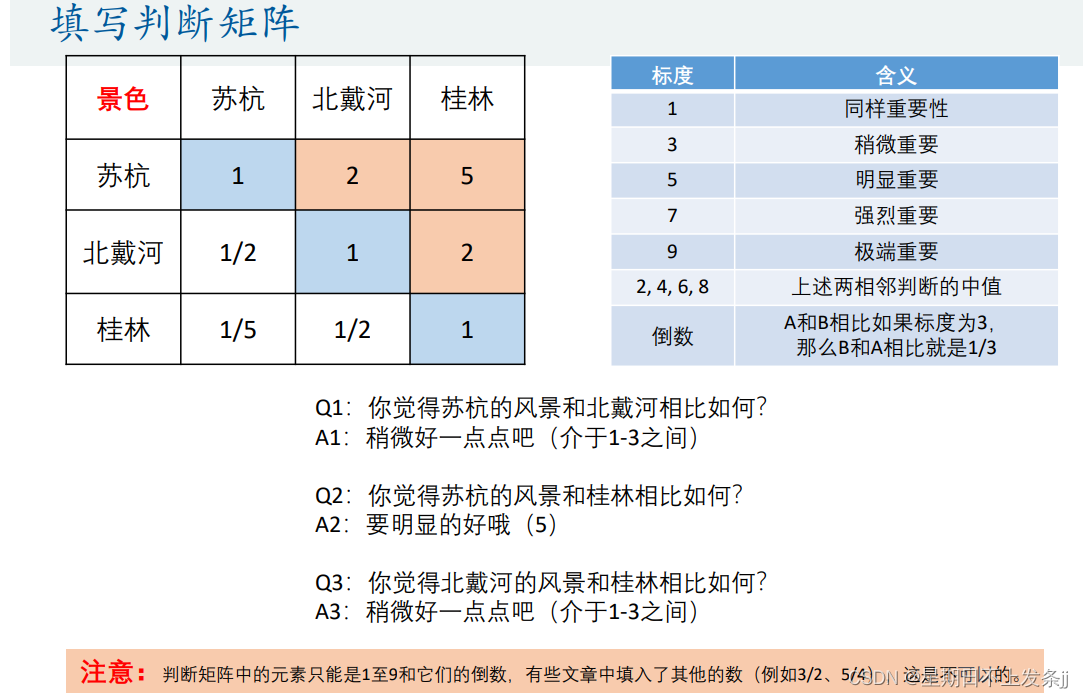
5.2 一致性检验

 

 

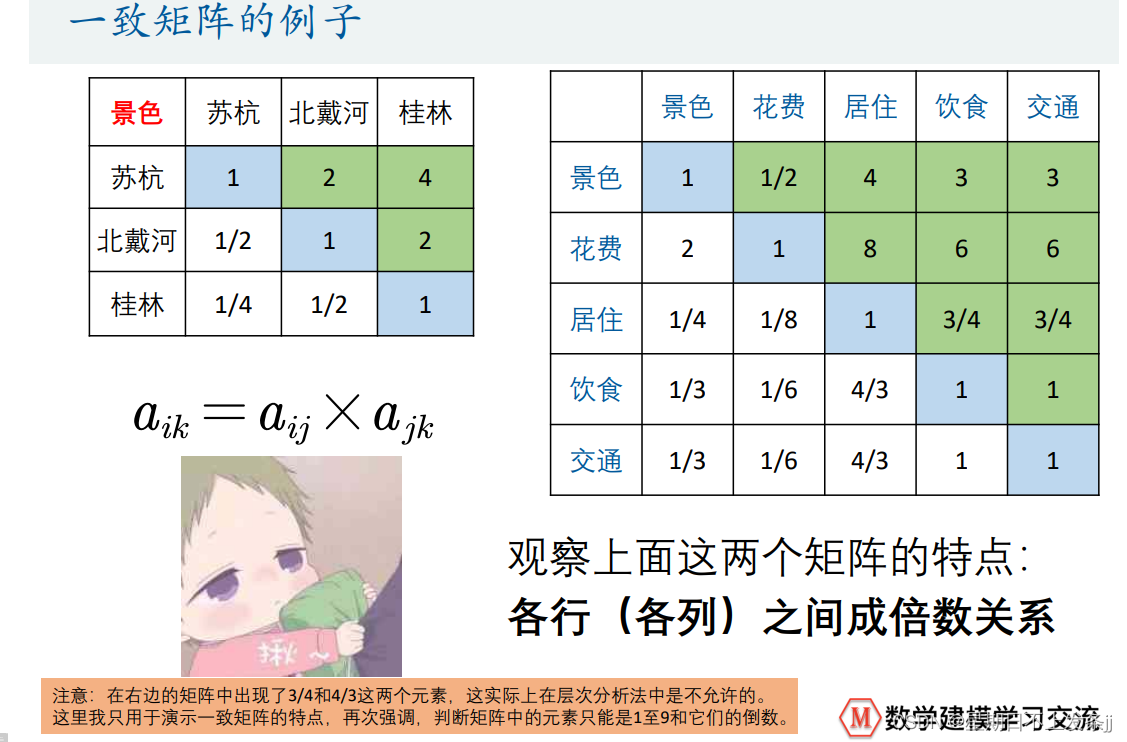
一致矩阵
若矩阵中每个元素aij > 0且满足aij*aji = 1 ，则我们称该矩阵为正互反矩阵。                                 在层次分析法中，我们构造的判断矩阵均是正互反矩阵；若正互反矩阵满足aij x ajk = aik， 则我们称其为一致矩阵。【注意，上述矩阵不是一致矩阵，需要进行一致性检验】
注意: 在使用判断矩阵求权重之前，必须对其进行一致性检验。

一致性检验的原理：（原理简略，具体步骤请去看清风数学建模的视频课）

 

 

这里有三种情况：1.判断矩阵是一致矩阵，也就是aij*ajk=aik，那么不需要进行一致性检验，可对该判断矩阵进行求权重；2.判断矩阵不是一致矩阵，但是经过检验认为该判断矩阵的一致性可以接受，则可对该判断矩阵进行求权重；3.判断矩阵不是一致矩阵，并且一致性也不能接受，那么需要对判断矩阵进行修正，比如“桂林景色跟苏杭景色一样”1改为“桂林景色比苏杭景色好”4。

5.3 判断矩阵求权重

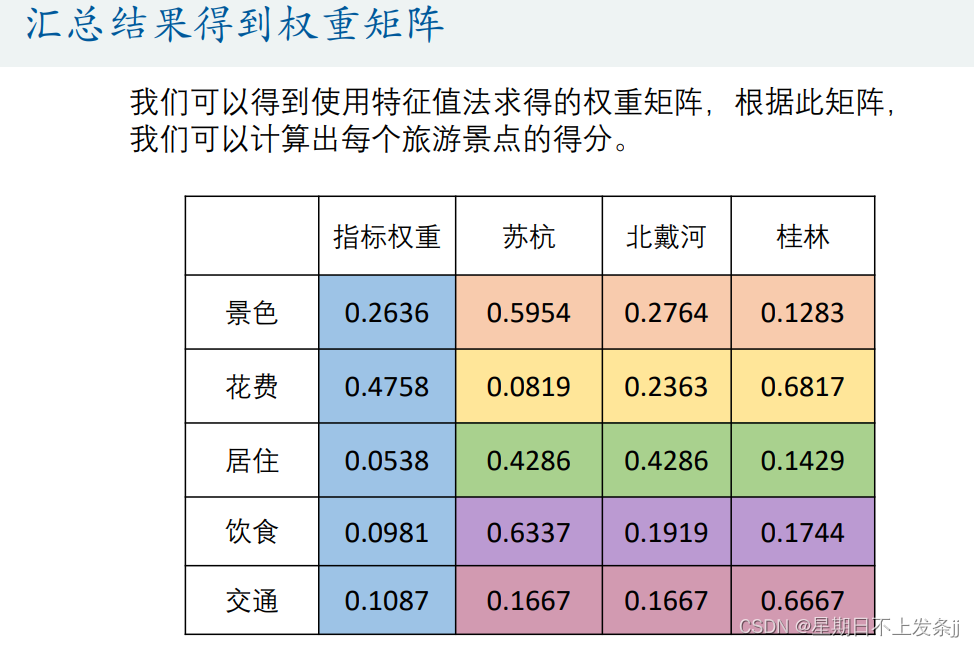
 step6：计算各方案的得分

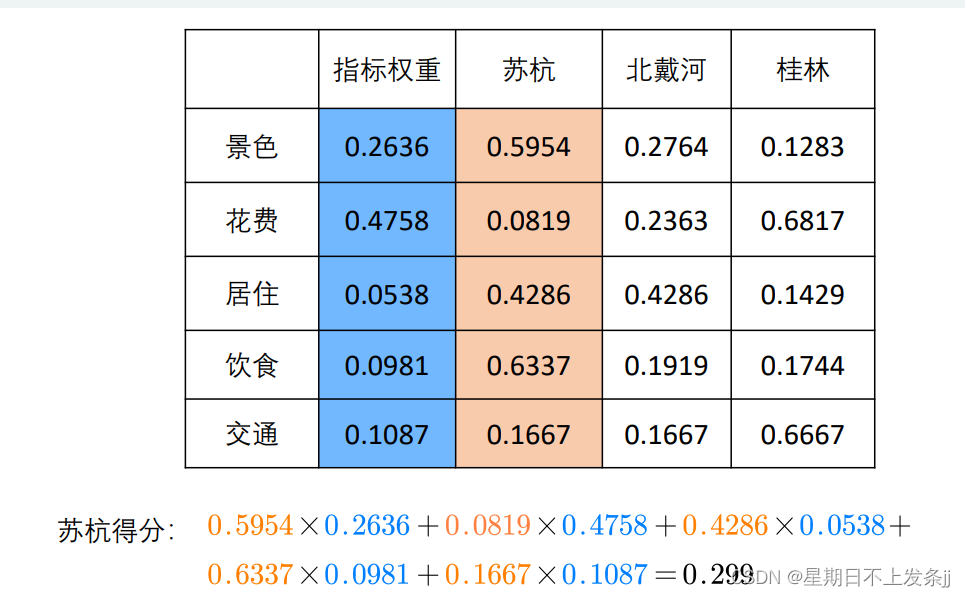
第二讲：层次分析法代码

层次分析法代码有三步：

1.填判断矩阵，判断矩阵可以自己来写，也可以专家来写，比赛时间紧张，一般自己来填。

2.判断是否是一致的。

3.计算权重，有三种方法计算权重：算术平均法、几何平均法、特征值法。

step1：输入判断矩阵

%% 输入判断矩阵
disp('请输入判断矩阵A： ')
% A = input('判断矩阵A=')
A =[1 1 4 1/3 3;
 1 1 4 1/3 3;
 1/4 1/4 1 1/3 1/2;
 3 3 3 1 3;
 1/3 1/3 2 1/3 1]
% matlab矩阵有两种写法，可以直接写到一行:
% [1 1 4 1/3 3;1 1 4 1/3 3;1/4 1/4 1 1/3 1/2;3 3 3 1 3;1/3 1/3 2 1/3 1]
% 也可以写成多行:
[1 1 4 1/3 3;
 1 1 4 1/3 3;
 1/4 1/4 1 1/3 1/2;
 3 3 3 1 3;
 1/3 1/3 2 1/3 1]
% 两行之间以分号结尾（最后一行的分号可加可不加），同行元素之间以空格（或者逗号）分开。

>> disp('请输入判断矩阵A： ')
请输入判断矩阵A： 
>> A =[1 1 4 1/3 3;1 1 4 1/3 3;1/4 1/4 1 1/3 1/2;3 3 3 1 3;1/3 1/3 2 1/3 1]A =1.0000    1.0000    4.0000    0.3333    3.00001.0000    1.0000    4.0000    0.3333    3.00000.2500    0.2500    1.0000    0.3333    0.50003.0000    3.0000    3.0000    1.0000    3.00000.3333    0.3333    2.0000    0.3333    1.0000

>> disp('请输入判断矩阵A： ')
请输入判断矩阵A： 
>>  [1 1 4 1/3 3;1 1 4 1/3 3;1/4 1/4 1 1/3 1/2;3 3 3 1 3;1/3 1/3 2 1/3 1]ans =1.0000    1.0000    4.0000    0.3333    3.00001.0000    1.0000    4.0000    0.3333    3.00000.2500    0.2500    1.0000    0.3333    0.50003.0000    3.0000    3.0000    1.0000    3.00000.3333    0.3333    2.0000    0.3333    1.0000

step2：判断是否一致

1.一致性检验的步骤

• 计算一致性指标   %注意，是最大特征值
• 查找对应的平均随机一致性指标RI

n	1	2	3	4	5	6	7	8	9	……
RI	0	0	0.52	0.89	1.12	1.26	1.36	1.41	1.46	……

%注意，RI最多支持n=15

• 计算一致性比例，

2.求最大特征值

A =[1 1 4 1/3 3;
 1 1 4 1/3 3;
 1/4 1/4 1 1/3 1/2;
 3 3 3 1 3;
 1/3 1/3 2 1/3 1]

[V,D] = eig(A)    %V是特征向量, D是由特征值构成的对角矩阵（除了对角线元素外，其余位置元素全为0）

>> A =[1 1 4 1/3 3;1 1 4 1/3 3;1/4 1/4 1 1/3 1/2;3 3 3 1 3;1/3 1/3 2 1/3 1]A =1.0000    1.0000    4.0000    0.3333    3.00001.0000    1.0000    4.0000    0.3333    3.00000.2500    0.2500    1.0000    0.3333    0.50003.0000    3.0000    3.0000    1.0000    3.00000.3333    0.3333    2.0000    0.3333    1.0000>> [V,D] = eig(A)V =0.4058 + 0.0000i  -0.0914 + 0.2754i  -0.0914 - 0.2754i   0.2298 + 0.0000i   0.7071 + 0.0000i0.4058 + 0.0000i  -0.0914 + 0.2754i  -0.0914 - 0.2754i   0.2298 + 0.0000i  -0.7071 + 0.0000i0.1299 + 0.0000i  -0.0268 - 0.1349i  -0.0268 + 0.1349i   0.3457 + 0.0000i  -0.0000 + 0.0000i0.7872 + 0.0000i   0.8930 + 0.0000i   0.8930 + 0.0000i  -0.6897 + 0.0000i   0.0000 + 0.0000i0.1847 + 0.0000i  -0.1131 - 0.0490i  -0.1131 + 0.0490i  -0.5470 + 0.0000i   0.0000 + 0.0000iD =5.2924 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i0.0000 + 0.0000i  -0.0843 + 1.2326i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0843 - 1.2326i   0.0000 + 0.0000i   0.0000 + 0.0000i0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.1238 + 0.0000i   0.0000 + 0.0000i0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i

%找出最大特征值 

Max_eig = max(max(D)) %也可以写成max(D(:))哦~

>> A =[1 1 4 1/3 3;1 1 4 1/3 3;1/4 1/4 1 1/3 1/2;3 3 3 1 3;1/3 1/3 2 1/3 1]A =1.0000    1.0000    4.0000    0.3333    3.00001.0000    1.0000    4.0000    0.3333    3.00000.2500    0.2500    1.0000    0.3333    0.50003.0000    3.0000    3.0000    1.0000    3.00000.3333    0.3333    2.0000    0.3333    1.0000>> [V,D] = eig(A)V =0.4058 + 0.0000i  -0.0914 + 0.2754i  -0.0914 - 0.2754i   0.2298 + 0.0000i   0.7071 + 0.0000i0.4058 + 0.0000i  -0.0914 + 0.2754i  -0.0914 - 0.2754i   0.2298 + 0.0000i  -0.7071 + 0.0000i0.1299 + 0.0000i  -0.0268 - 0.1349i  -0.0268 + 0.1349i   0.3457 + 0.0000i  -0.0000 + 0.0000i0.7872 + 0.0000i   0.8930 + 0.0000i   0.8930 + 0.0000i  -0.6897 + 0.0000i   0.0000 + 0.0000i0.1847 + 0.0000i  -0.1131 - 0.0490i  -0.1131 + 0.0490i  -0.5470 + 0.0000i   0.0000 + 0.0000iD =5.2924 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i0.0000 + 0.0000i  -0.0843 + 1.2326i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0843 - 1.2326i   0.0000 + 0.0000i   0.0000 + 0.0000i0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.1238 + 0.0000i   0.0000 + 0.0000i0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i>> max(D)ans =5.2924 + 0.0000i  -0.0843 + 1.2326i  -0.0843 - 1.2326i  -0.1238 + 0.0000i   0.0000 + 0.0000i>> max(max(D))ans =5.2924>> D(:)ans =5.2924 + 0.0000i0.0000 + 0.0000i0.0000 + 0.0000i0.0000 + 0.0000i0.0000 + 0.0000i0.0000 + 0.0000i-0.0843 + 1.2326i0.0000 + 0.0000i0.0000 + 0.0000i0.0000 + 0.0000i0.0000 + 0.0000i0.0000 + 0.0000i-0.0843 - 1.2326i0.0000 + 0.0000i0.0000 + 0.0000i0.0000 + 0.0000i0.0000 + 0.0000i0.0000 + 0.0000i-0.1238 + 0.0000i0.0000 + 0.0000i0.0000 + 0.0000i0.0000 + 0.0000i0.0000 + 0.0000i0.0000 + 0.0000i0.0000 + 0.0000i>> max(D(:))ans =5.2924>> Max_eig = max(max(D))Max_eig =5.2924>> 

3.求矩阵的n

[n,n] = size(A)  

% 也可以写成n = size(A,1)
% 因为我们的判断矩阵A是一个方阵，所以这里的r和c相同，我们可以就用同一个字母n表示

>> [n,n] = size(A)n =5n =5>> n = size(A,1)n =5

3.计算一致性指标CI

CI = (Max_eig - n) / (n-1)

>> A =[1 1 4 1/3 3;1 1 4 1/3 3;1/4 1/4 1 1/3 1/2;3 3 3 1 3;1/3 1/3 2 1/3 1]A =1.0000    1.0000    4.0000    0.3333    3.00001.0000    1.0000    4.0000    0.3333    3.00000.2500    0.2500    1.0000    0.3333    0.50003.0000    3.0000    3.0000    1.0000    3.00000.3333    0.3333    2.0000    0.3333    1.0000>> [V,D] = eig(A)V =0.4058 + 0.0000i  -0.0914 + 0.2754i  -0.0914 - 0.2754i   0.2298 + 0.0000i   0.7071 + 0.0000i0.4058 + 0.0000i  -0.0914 + 0.2754i  -0.0914 - 0.2754i   0.2298 + 0.0000i  -0.7071 + 0.0000i0.1299 + 0.0000i  -0.0268 - 0.1349i  -0.0268 + 0.1349i   0.3457 + 0.0000i  -0.0000 + 0.0000i0.7872 + 0.0000i   0.8930 + 0.0000i   0.8930 + 0.0000i  -0.6897 + 0.0000i   0.0000 + 0.0000i0.1847 + 0.0000i  -0.1131 - 0.0490i  -0.1131 + 0.0490i  -0.5470 + 0.0000i   0.0000 + 0.0000iD =5.2924 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i0.0000 + 0.0000i  -0.0843 + 1.2326i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0843 - 1.2326i   0.0000 + 0.0000i   0.0000 + 0.0000i0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.1238 + 0.0000i   0.0000 + 0.0000i0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i>> Max_eig = max(max(D))Max_eig =5.2924>> [n,n] = size(A)n =5n =5>> Max_eigMax_eig =5.2924>> nn =5>> CI = (Max_eig - n) / (n-1)CI =0.0731

4.查找对应的平均随机一致性指标RI

%把RI储存到MATLAB里

RI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59];  

%注意哦，这里的RI最多支持 n = 15

CR=CI/RI(n)

%RI(n)是取第n个元素的意思

>> RI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59]RI =0         0    0.5200    0.8900    1.1200    1.2600    1.3600    1.4100    1.4600    1.4900    1.5200    1.5400    1.5600    1.5800    1.5900>> RI(n)ans =1.1200

5.计算一致性比例CR

 CI = (Max_eig - n) / (n-1);
RI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59];  %注意哦，这里的RI最多支持 n = 15
CR=CI/RI(n);
disp('一致性指标CI=');disp(CI);
disp('一致性比例CR=');disp(CR);
if CR<0.10
    disp('因为CR < 0.10，所以该判断矩阵A的一致性可以接受!');
else
    disp('注意：CR >= 0.10，因此该判断矩阵A需要进行修改!');
end

>> CR=CI/RI(n)CR =0.0653>> disp('一致性指标CI=');disp(CI);
disp('一致性比例CR=');disp(CR);
if CR<0.10disp('因为CR < 0.10，所以该判断矩阵A的一致性可以接受!');
elsedisp('注意：CR >= 0.10，因此该判断矩阵A需要进行修改!');
end
一致性指标CI=0.0731一致性比例CR=0.0653因为CR < 0.10，所以该判断矩阵A的一致性可以接受!

step3：计算权重

1.算术平均法求权重

算术平均值法求权重的步骤：

• 将判断矩阵按照列归一化（每一个元素初一其所在列的和）
• 将归一化的各列相加（按行求和）
• 将相加后得到的向量中每个元素除以n，得到权重向量

% 第一步：将判断矩阵按照列归一化（每一个元素除以其所在列的和）
Sum_A = sum(A)

[n,n] = size(A)  % 也可以写成n = size(A,1)
% 因为我们的判断矩阵A是一个方阵，所以这里的r和c相同，我们可以就用同一个字母n表示

SUM_A = repmat(Sum_A,n,1)   %repeat matrix的缩写

Stand_A = A ./ SUM_A
% 这里我们直接将两个矩阵对应的元素相除即可

>> Sum_A = sum(A)Sum_A =5.5833    5.5833   14.0000    2.3333   10.5000>> [n,n] = size(A)n =5n =5>> SUM_A = repmat(Sum_A,n,1)SUM_A =5.5833    5.5833   14.0000    2.3333   10.50005.5833    5.5833   14.0000    2.3333   10.50005.5833    5.5833   14.0000    2.3333   10.50005.5833    5.5833   14.0000    2.3333   10.50005.5833    5.5833   14.0000    2.3333   10.5000>> Stand_A = A ./ SUM_AStand_A =0.1791    0.1791    0.2857    0.1429    0.28570.1791    0.1791    0.2857    0.1429    0.28570.0448    0.0448    0.0714    0.1429    0.04760.5373    0.5373    0.2143    0.4286    0.28570.0597    0.0597    0.1429    0.1429    0.0952

% 第二步：将归一化的各列相加(按行求和)
sum(Stand_A,2)

>> Stand_A = A ./ SUM_AStand_A =0.1791    0.1791    0.2857    0.1429    0.28570.1791    0.1791    0.2857    0.1429    0.28570.0448    0.0448    0.0714    0.1429    0.04760.5373    0.5373    0.2143    0.4286    0.28570.0597    0.0597    0.1429    0.1429    0.0952>> sum(Stand_A,2)ans =1.07251.07250.35152.00320.5004

% 第三步：将相加后得到的向量中每个元素除以n即可得到权重向量
disp('算术平均法求权重的结果为：');
disp(sum(Stand_A,2) / n)
% 首先对标准化后的矩阵按照行求和，得到一个列向量
% 然后再将这个列向量的每个元素同时除以n即可（注意这里也可以用./哦）

>> Stand_A = A ./ SUM_AStand_A =0.1791    0.1791    0.2857    0.1429    0.28570.1791    0.1791    0.2857    0.1429    0.28570.0448    0.0448    0.0714    0.1429    0.04760.5373    0.5373    0.2143    0.4286    0.28570.0597    0.0597    0.1429    0.1429    0.0952>> sum(Stand_A,2)ans =1.07251.07250.35152.00320.5004>> disp('算术平均法求权重的结果为：');
disp(sum(Stand_A,2) / n)
算术平均法求权重的结果为：0.21450.21450.07030.40060.1001

2.几何平均值法求权重

几何平均法求权重的步骤：

• 将A的元素按照行相乘得到一个新的列向量
• 将新的向量的每个向量开n次方
• 对该列向量进行归一化即可得到权重向量

% 第一步：将A的元素按照行相乘得到一个新的列向量
clc;A
Prduct_A = prod(A,2)
% prod函数和sum函数类似，一个用于乘，一个用于加  dim = 2 维度是行

>> A
Prduct_A = prod(A,2)A =1.0000    1.0000    4.0000    0.3333    3.00001.0000    1.0000    4.0000    0.3333    3.00000.2500    0.2500    1.0000    0.3333    0.50003.0000    3.0000    3.0000    1.0000    3.00000.3333    0.3333    2.0000    0.3333    1.0000Prduct_A =4.00004.00000.010481.00000.0741

% 第二步：将新的向量的每个分量开n次方
Prduct_n_A = Prduct_A .^ (1/n)
% 这里对每个元素进行乘方操作，因此要加.号哦。  ^符号表示乘方哦  这里是开n次方，所以我们等价求1/n次方

>> Prduct_n_A = Prduct_A .^ (1/n)Prduct_n_A =1.31951.31950.40142.40820.5942

% 第三步：对该列向量进行归一化即可得到权重向量
% 将这个列向量中的每一个元素除以这一个向量的和即可
disp('几何平均法求权重的结果为：');
disp(Prduct_n_A ./ sum(Prduct_n_A))

>> disp('几何平均法求权重的结果为：');
disp(Prduct_n_A ./ sum(Prduct_n_A))
几何平均法求权重的结果为：0.21840.21840.06640.39850.0983>> 

3.特征值法求权重

特征值法求权重的步骤：

• 求出矩阵A的最大特征值及其对应的特征向量
• 对求出的特征向量进行归一化即可得到权重向量

% 第一步：求出矩阵A的最大特征值以及其对应的特征向量
clc
[V,D] = eig(A)    %V是特征向量, D是由特征值构成的对角矩阵（除了对角线元素外，其余位置元素全为0）
Max_eig = max(max(D)) %也可以写成max(D(:))哦~

>> [V,D] = eig(A)V =0.4058 + 0.0000i  -0.0914 + 0.2754i  -0.0914 - 0.2754i   0.2298 + 0.0000i   0.7071 + 0.0000i0.4058 + 0.0000i  -0.0914 + 0.2754i  -0.0914 - 0.2754i   0.2298 + 0.0000i  -0.7071 + 0.0000i0.1299 + 0.0000i  -0.0268 - 0.1349i  -0.0268 + 0.1349i   0.3457 + 0.0000i  -0.0000 + 0.0000i0.7872 + 0.0000i   0.8930 + 0.0000i   0.8930 + 0.0000i  -0.6897 + 0.0000i   0.0000 + 0.0000i0.1847 + 0.0000i  -0.1131 - 0.0490i  -0.1131 + 0.0490i  -0.5470 + 0.0000i   0.0000 + 0.0000iD =5.2924 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i0.0000 + 0.0000i  -0.0843 + 1.2326i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0843 - 1.2326i   0.0000 + 0.0000i   0.0000 + 0.0000i0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.1238 + 0.0000i   0.0000 + 0.0000i0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i>> Max_eig = max(max(D))Max_eig =5.2924>> 

% 那么怎么找到最大特征值所在的位置了？ 需要用到find函数，它可以用来返回向量或者矩阵中不为0的元素的位置索引。
% 那么问题来了，我们要得到最大特征值的位置，就需要将包含所有特征值的这个对角矩阵D中，不等于最大特征值的位置全变为0
% 这时候可以用到矩阵与常数的大小判断运算
D == Max_eig
[r,c] = find(D == Max_eig , 1)
% 找到D中第一个与最大特征值相等的元素的位置，记录它的行和列。

>> [V,D] = eig(A)V =0.4058 + 0.0000i  -0.0914 + 0.2754i  -0.0914 - 0.2754i   0.2298 + 0.0000i   0.7071 + 0.0000i0.4058 + 0.0000i  -0.0914 + 0.2754i  -0.0914 - 0.2754i   0.2298 + 0.0000i  -0.7071 + 0.0000i0.1299 + 0.0000i  -0.0268 - 0.1349i  -0.0268 + 0.1349i   0.3457 + 0.0000i  -0.0000 + 0.0000i0.7872 + 0.0000i   0.8930 + 0.0000i   0.8930 + 0.0000i  -0.6897 + 0.0000i   0.0000 + 0.0000i0.1847 + 0.0000i  -0.1131 - 0.0490i  -0.1131 + 0.0490i  -0.5470 + 0.0000i   0.0000 + 0.0000iD =5.2924 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i0.0000 + 0.0000i  -0.0843 + 1.2326i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0843 - 1.2326i   0.0000 + 0.0000i   0.0000 + 0.0000i0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.1238 + 0.0000i   0.0000 + 0.0000i0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i>> max(D)ans =5.2924 + 0.0000i  -0.0843 + 1.2326i  -0.0843 - 1.2326i  -0.1238 + 0.0000i   0.0000 + 0.0000i>> max(max(D))ans =5.2924>> Max_eig = max(max(D))Max_eig =5.2924>> DD =5.2924 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i0.0000 + 0.0000i  -0.0843 + 1.2326i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0843 - 1.2326i   0.0000 + 0.0000i   0.0000 + 0.0000i0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.1238 + 0.0000i   0.0000 + 0.0000i0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i>> D == Max_eigans =1     0     0     0     00     0     0     0     00     0     0     0     00     0     0     0     00     0     0     0     0>> [r,c] = find(D == Max_eig , 1)r =1c =1>> 

% 第二步：对求出的特征向量进行归一化即可得到我们的权重
V(:,c)
disp('特征值法求权重的结果为：');
disp( V(:,c) ./ sum(V(:,c)) )
% 我们先根据上面找到的最大特征值的列数c找到对应的特征向量，然后再进行标准化。

>> VV =0.4058 + 0.0000i  -0.0914 + 0.2754i  -0.0914 - 0.2754i   0.2298 + 0.0000i   0.7071 + 0.0000i0.4058 + 0.0000i  -0.0914 + 0.2754i  -0.0914 - 0.2754i   0.2298 + 0.0000i  -0.7071 + 0.0000i0.1299 + 0.0000i  -0.0268 - 0.1349i  -0.0268 + 0.1349i   0.3457 + 0.0000i  -0.0000 + 0.0000i0.7872 + 0.0000i   0.8930 + 0.0000i   0.8930 + 0.0000i  -0.6897 + 0.0000i   0.0000 + 0.0000i0.1847 + 0.0000i  -0.1131 - 0.0490i  -0.1131 + 0.0490i  -0.5470 + 0.0000i   0.0000 + 0.0000i>> [r,c] = find(D == Max_eig , 1)r =1c =1>> cc =1>> V(:,c)ans =0.40580.40580.12990.78720.1847>> sum(V(:,c))ans =1.9134>> disp('特征值法求权重的结果为：');
disp( V(:,c) ./ sum(V(:,c)) )
特征值法求权重的结果为：0.21210.21210.06790.41140.0965>> 

step4：把权重复制到excel表格中去

算术平均值法	几何平均值法	特征值法
0.2145     0.2145     0.0703     0.4006     0.1001	0.2184     0.2184     0.0664     0.3985     0.0983	0.2121     0.2121     0.0679     0.4114     0.0965

第三讲：层次分析法作业

恳请大家批评指正！层次分析法的完整代码有需要的可以找我分享，这里就不过多赘述了。

1. 你要购置一台个人电脑，考虑功能、价格等因素，如何作出决策。

首先想到三个问题：

1. 评价目标？

购买一个联想笔记本电脑。

1. 为了达到目标有几种可选择的方案？

小新16锐龙、小新Pro14锐龙、小新Pro16酷睿

1. 评价的准则或指标是什么？

经查阅相关资料，评价标准有：功能、价格、外观。

权重表格

	指标权重	小新16锐龙	小新Pro14锐龙	小新Pro16酷睿
功能
价格
外观

（一）评价准则的判断矩阵

标度	含义
1	同样重要
3	稍微重要
5	明显重要
7	强烈重要
9	极端重要
2，4，6，8	上述两相邻判断的中值
标度	含义

	功能	价格	外观
功能	1	2	5
价格	1/2	1	4
外观	1/5	1/4	1

比赛时间很紧张，一般是自己填写

通过一致性检验

计算权重

1. 算术平均法

算术平均法求权重的结果为：

    0.5679

    0.3339

    0.0982

1. 几何平均法

几何平均法求权重的结果为：

    0.5695

    0.3331

    0.0974

1. 特征值法

特征值法求权重的结果为：

    0.5695

    0.3331

    0.0974

评价准则的权重

	算术平均值法	几何平均值法	特征值法
功能	0.5679	0.5695	0.5695
价格	0.3339	0.3331	0.3331
外观	0.0982	0.0974	0.0974

（二）方案的判断矩阵

	指标权重	小新16锐龙	小新Pro14锐龙	小新Pro16酷睿
功能
价格
外观

功能	小新16锐龙	小新Pro14锐龙	小新Pro16酷睿
小新16锐龙	1	1/2	1/5
小新Pro14锐龙	2	1	1/3
小新Pro16酷睿	5	3	1

价格	小新16锐龙	小新Pro14锐龙	小新Pro16酷睿
小新16锐龙	1	2	4
小新Pro14锐龙	1/2	1	3
小新Pro16酷睿	1/4	1/3	1

外观	小新16锐龙	小新Pro14锐龙	小新Pro16酷睿
小新16锐龙	1	1/2	1/5
小新Pro14锐龙	2	1	1/3
小新Pro16酷睿	5	3	1

比赛时间很紧张，一般是自己填写

通过一致性检验

计算权重

功能权重	算术	几何	特征值
小新16锐龙	0.1222	0.1220	0.1220
小新Pro14锐龙	0.2299	0.2297	0.2297
小新Pro16酷睿	0.6479	0.6483	0.6483

价格权重	算术	几何	特征值
小新16锐龙	0.5571	0.5584	0.5584
小新Pro14锐龙	0.3202	0.3196	0.3196
小新Pro16酷睿	0.1226	0.1220	0.1220

外观权重	算术	几何	特征值
小新16锐龙	0.1222	0.1220	0.1220
小新Pro14锐龙	0.2299	0.2297	0.2297
小新Pro16酷睿	0.6479	0.6483	0.6483

选取特征值法求得的权重

	指标权重	小新16锐龙	小新Pro14锐龙	小新Pro16酷睿
功能	0.5695	0.1220	0.2297	0.6483
价格	0.3331	0.5584	0.3196	0.1220
外观	0.0974	0.1220	0.2297	0.6483

计算

小新16锐龙=0.267365

小新Pro14锐龙=0.259646

小新Pro16酷睿=0.472989

因此，选择小新Pro16酷睿