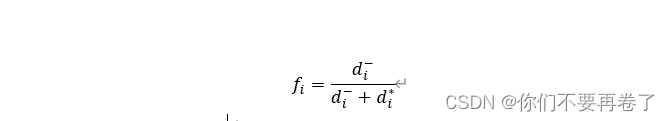本文主要是介绍TOPSIS 法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
TOPSIS法(Technique for Order Preference by Similarity to Ideal Solution)是一种多属性决策方法,用于评估和选择最佳决策方案。该方法基于两个关键概念:相似度和理想解。
在TOPSIS方法中,首先将决策方案的各个属性进行归一化处理,然后计算每个方案与理想解之间的距离。距离可以根据不同的决策问题选择不同的度量方法,例如欧氏距离、曼哈顿距离等。
之后,根据每个方案与理想解之间的距离,计算每个方案的接近度。接近度可以根据距离进行计算,例如距离越小,接近度越高。最后,根据每个方案的接近度进行排序,从而确定最佳的决策方案。
TOPSIS方法在多属性决策问题中广泛应用,特别是在供应链管理、项目管理和产品选择等领域。它能够综合考虑多个属性,并提供一个客观的评价和选择方法。
TOPSIS (Technique for Order Preference by Similarity to Ideal Solution) 法是一种多属性决策方法,其原理是通过比较候选解与理想解之间的相似性来进行排序。该方法基于以下假设:
1. 候选解是由多个属性构成的。每个属性可以是量化的,也可以是定性的。
2. 每个属性都有一个重要程度权重,用于指示其在决策中的相对重要性。这些权重可以根据决策者的主观判断或通过某种数学方法确定。
基于这些假设,TOPSIS 方法的基本原理如下:
1. 确定理想解:对于每个属性,找到一个最佳解和一个最差解。最佳解是在每个属性上取得最大值的解,而最差解是在每个属性上取得最小值的解。
2. 计算候选解与理想解之间的相似性:使用某种相似性度量(例如欧氏距离或曼哈顿距离),计算候选解与最佳解之间的距离和候选解与最差解之间的距离。
3. 确定相对接近程度:根据候选解与最佳解之间的距离和候选解与最差解之间的距离,计算候选解与理想解之间的相对接近程度。
4. 排序:根据候选解与理想解之间的相对接近程度,按照从高到低的顺序对候选解进行排序。相对接近程度越高,意味着候选解越接近理想解。
通过TOPSIS方法,决策者可以将候选解进行排名,从而选择出最优解来满足其需求。
TOPSIS(Technique for Order Preference by Similarity to Ideal Solution)法是一种多属性决策方法,用于选择最佳的方案。该方法要求数据具有以下特点:
1. 属性值要求数值化:TOPSIS法只适用于数值型数据,因此属性值需要能够量化和比较。
2. 正向指标和负向指标:数据需要能够分为正向指标和负向指标。正向指标是越大越好的指标,而负向指标是越小越好的指标。例如,成本是一个负向指标,利润是一个正向指标。
3. 属性值需为连续型:TOPSIS法假设属性值是连续的,因此离散型数据需要进行转换或者分段处理。
4. 同等权重:TOPSIS法假设各属性具有同等权重,即没有明确的权重比例。如果有明确的权重比例要求,需要进行额外的处理。
5. 数据完整性和一致性:数据需要完整且一致,即没有缺失值或冲突值。
6. 适用于决策问题:TOPSIS法适用于具有多个属性,需要从多个候选方案中选择最佳方案的决策问题。
7. 属性之间相互独立:TOPSIS法假设属性之间相互独立,即属性之间的变化不会互相影响。
具备以上特点的数据可以使用TOPSIS法进行多属性决策。
TOPSIS方法适用于以下场景:
1. 多属性决策:TOPSIS方法适用于需要考虑多个属性或指标的决策问题。它可以帮助决策者将不同属性的影响综合起来,进行综合评估。
2. 供应链管理:在供应链管理中,需要选择最优供应商或最佳物流方案。TOPSIS方法可以帮助评估不同供应商或物流方案在多个属性上的表现,从而选择最佳方案。
3. 项目选择:在项目管理中,需要选择最具优势的项目方案。TOPSIS方法可以帮助评估不同项目方案在多个关键指标上的表现,从而选择最佳项目。
4. 产品或服务评估:在市场竞争中,需要评估产品或服务的优劣。TOPSIS方法可以帮助评估不同产品或服务在多个关键属性上的表现,从而确定市场竞争力。
5. 城市规划:在城市规划中,需要评估不同规划方案的综合效益。TOPSIS方法可以帮助评估不同规划方案在多个指标上的表现,从而选择最佳规划方案。
总之,TOPSIS方法适用于需要综合考虑多个属性或指标的决策问题,可以应用于各种领域的决策分析。
在TOPSIS方法中,权重的确定通常是根据专家判断或者利用主观评价的方法确定的。下面是一种常见的确定权重的方法:
1. 构建评价指标体系:首先需要确定一组评价指标来衡量待评价对象的各个方面。这些指标应该具有客观性、可测量性和可比较性,以便能够进行权重的确定。
2. 收集数据:对于每个评价指标,需要收集相关的数据来进行评价。这可以通过实地调研、问卷调查、统计数据等方式来获取。
3. 标准化数据:由于不同的评价指标往往具有不同的量纲和范围,需要将数据进行标准化处理,以确保不同指标的权重可以进行比较。常用的标准化方法有最大-最小标准化和标准差标准化等。
4. 确定权重:根据专家判断或者利用主观评价的方法来确定各个评价指标的权重。可以通过专家访谈、专家打分、模糊层次分析法等方法来进行权重的确定。
5. 计算最终权重:将确定的权重与标准化后的数据相乘,得到各个评价指标的加权得分。然后可以根据TOPSIS方法的计算公式进行计算,得到各个待评价对象的综合得分,从而进行排序和比较。
需要注意的是,权重的确定往往具有一定的主观性,因此应该尽量多收集专家意见、进行敏感性分析等,以提高权重的可靠性和准确性。
TOPSIS熵权法是一种多属性决策方法,用于评价多个候选方案的综合性能。TOPSIS是Technique for Order Preference by Similarity to Ideal Solution的缩写,意为“相对理想解的相似性排序法”。
TOPSIS熵权法的基本思想是将每个属性的权重根据其对决策结果的重要性来确定。传统的TOPSIS方法中,属性权重是根据主观判断或专家意见来确定的,但这种方法可能具有主观性和不可靠性。为了解决这个问题,熵权法在TOPSIS中引入了信息熵的概念,通过计算属性的熵值来确定属性的权重。
具体来说,熵权法根据每个属性的信息熵计算出属性的权重,信息熵用来表示属性的不确定性和多样性。属性的熵值越大,表示属性的多样性越高,对决策结果的影响也越大,因此其权重也越大。
熵权法的步骤如下:
1. 收集属性数据并归一化。
2. 计算每个属性的信息熵。
3. 根据信息熵计算每个属性的权重。
4. 根据归一化处理后的属性数据,计算每个候选方案与理想解的相似性度量值。
5. 根据相似性度量值对候选方案进行排序,得到最终的综合评价结果。
TOPSIS熵权法能够综合考虑多个属性的权重,提高决策的客观性和可靠性。在实际决策问题中,可以使用TOPSIS熵权法来评价候选方案的优劣,帮助决策者做出正确的决策。
下面是一个示例代码,用于实现TOPSIS熵权法:
```python
import numpy as np
# 计算熵值权重
def entropy_weights(matrix):
m, n = matrix.shape
# 计算每个指标的熵
entropy = np.zeros(n)
for i in range(n):
p = matrix[:, i] / sum(matrix[:, i])
entropy[i] = -sum(p * np.log2(p))
# 计算熵权重
weights = (1 - entropy) / sum(1 - entropy)
return weights
# 计算正理想解和负理想解
def ideal_solution(matrix, weights):
m, n = matrix.shape
# 归一化
normalized_matrix = matrix / np.sqrt(np.sum(matrix**2, axis=0))
# 计算正理想解
positive_ideal_solution = np.max(normalized_matrix, axis=0)
# 计算负理想解
negative_ideal_solution = np.min(normalized_matrix, axis=0)
# 加权
positive_ideal_solution = positive_ideal_solution * weights
negative_ideal_solution = negative_ideal_solution * weights
return positive_ideal_solution, negative_ideal_solution
# 计算每个方案的综合评价指数
def topsis(matrix, weights, positive_ideal_solution, negative_ideal_solution):
m, n = matrix.shape
# 归一化
normalized_matrix = matrix / np.sqrt(np.sum(matrix**2, axis=0))
# 计算每个方案的综合评价指数
topsis_score = np.zeros(m)
for i in range(m):
topsis_score[i] = np.sqrt(np.sum((normalized_matrix[i] - positive_ideal_solution)**2)) / \
(np.sqrt(np.sum((normalized_matrix[i] - positive_ideal_solution)**2)) + \
np.sqrt(np.sum((normalized_matrix[i] - negative_ideal_solution)**2)))
return topsis_score
# 测试数据
matrix = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
weights = entropy_weights(matrix)
positive_ideal_solution, negative_ideal_solution = ideal_solution(matrix, weights)
topsis_score = topsis(matrix, weights, positive_ideal_solution, negative_ideal_solution)
print("权重:", weights)
print("正理想解:", positive_ideal_solution)
print("负理想解:", negative_ideal_solution)
print("TOPSIS综合评价指数:", topsis_score)
```
上述代码实现了TOPSIS熵权法的计算过程。首先,计算熵权重的函数entropy_weights()根据熵的定义计算每个指标的熵,并将熵值转化为权重;然后,通过函数ideal_solution()计算正理想解和负理想解,首先对原始矩阵归一化,然后计算正理想解为每列最大值乘以权重,负理想解为每列最小值乘以权重;最后,通过函数topsis()计算每个方案的综合评价指数,按照公式计算每个方案到正理想解的距离和到负理想解的距离,然后根据距离计算综合评价指数。
这篇关于TOPSIS 法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!