优劣解距离法（TOPSIS）

方法步骤

1.将原始矩阵正向化
最常见的四种指标：
原始矩阵正向化的本质其实是要将所有的指标类型统一转化为极大型指标。
极小型指标 -> 极大型指标
公式：max - x
如果所有元素均为正数，那么也可以使用1/x。
中间型指标 -> 极大型指标
中间型指标：指标值既不要太大，也不要太小，去某特定值最好（如水质量评估PH值）
公式：

区间型指标 -> 极大型指标
区间型指标： 指标值落在某个区间内最好，例如人的体温在36°～ 37°这个区间比较好。
{xi}是一组区间型指标序列，且最佳的区间为[a,b]，那么正向化的公式如下：


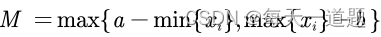
2.正向矩阵标准化
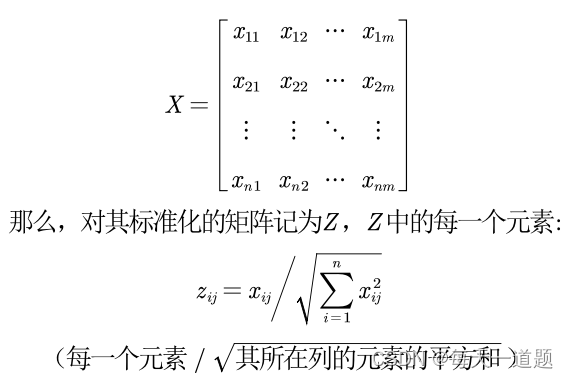
假设有n个要评价的对象，m个评价指标（已经正向化了）构成的正向矩阵如下：

3.计算得分并归一化
公式：z与最小值的距离/z与最大值的距离 + z与最小值的距离
首先找到最大每一列的最大值Z+，然后再找到每一列的最小值Z-，然后
最后将得分归一化即可。

代码

数据如下:

把数据复制到工作区，然后将数据另存为与代码相同的一个文件夹命名为shuju.mat，然后运行代码：

load shuju.mat

正向化：
1.极小型指标 -> 极大型指标函数：

function [posit_x] = Min2Max(x)posit_x = max(x) - x;
end

2.中间型指标 -> 极大型指标函数：

function [posit_x] = Mid2Max(x,best)M =  max(abs(x - best));posit_x = 1 - abs(x - best) / M;
end

3.区间型指标 -> 极大型指标函数：

function [posit_x] = Inter2Max(x,a,b)r_x = size(x,1);M = max([a - min(x),max(x) - b]);posit_x = zeros(r_x,1);for i = 1:r_xif x(i) < aposit_x(i) = 1 - (a - x(i)) / M;elseif x(i) > bposit_x(i) = 1 - (x(i) - b) / M;elseposit_x(i) = 1;endend
end

正向化函数：

function [posit_x] = Positivization(x,type,i)
% 输入变量有三个：
% x：需要正向化处理的指标对应的原始列向量
% type： 指标的类型（1：极小型， 2：中间型， 3：区间型）
% i: 正在处理的是原始矩阵中的哪一列
% 输出变量posit_x表示：正向化后的列向量if type == 1  %极小型disp(['第' num2str(i) '列是极小型，正在正向化'] )posit_x = Min2Max(x);  %调用Min2Max函数来正向化disp(['第' num2str(i) '列极小型正向化处理完成'] )disp('~~~~~~~~~~~~~~~~~~~~分界线~~~~~~~~~~~~~~~~~~~~')elseif type == 2  %中间型disp(['第' num2str(i) '列是中间型'] )best = input('请输入最佳的那一个值： ');posit_x = Mid2Max(x,best);disp(['第' num2str(i) '列中间型正向化处理完成'] )disp('~~~~~~~~~~~~~~~~~~~~分界线~~~~~~~~~~~~~~~~~~~~')elseif type == 3  %区间型disp(['第' num2str(i) '列是区间型'] )a = input('请输入区间的下界： ');b = input('请输入区间的上界： '); posit_x = Inter2Max(x,a,b);disp(['第' num2str(i) '列区间型正向化处理完成'] )disp('~~~~~~~~~~~~~~~~~~~~分界线~~~~~~~~~~~~~~~~~~~~')elsedisp('没有这种类型的指标，请检查Type向量中是否有除了1、2、3之外的其他值')end
end

总函数：

[n,m] = size(X);
disp(['共有' num2str(n) '个评价对象, ' num2str(m) '个评价指标']) 
Judge = input(['这' num2str(m) '个指标是否需要经过正向化处理，需要请输入1 ，不需要输入0：  ']);if Judge == 1Position = input('请输入需要正向化处理的指标所在的列，例如第2、3、6三列需要处理，那么你需要输入[2,3,6]： '); %[2,3,4]disp('请输入需要处理的这些列的指标类型（1：极小型， 2：中间型， 3：区间型） ')Type = input('例如：第2列是极小型，第3列是区间型，第6列是中间型，就输入[1,3,2]：  '); %[2,1,3]% 注意，Position和Type是两个同维度的行向量for i = 1 : size(Position,2)  %这里需要对这些列分别处理，因此我们需要知道一共要处理的次数，即循环的次数X(:,Position(i)) = Positivization(X(:,Position(i)),Type(i),Position(i));% Positivization是我们自己定义的函数，其作用是进行正向化，其一共接收三个参数% 第一个参数是要正向化处理的那一列向量 X(:,Position(i))   回顾上一讲的知识，X(:,n)表示取第n列的全部元素% 第二个参数是对应的这一列的指标类型（1：极小型， 2：中间型， 3：区间型）% 第三个参数是告诉函数我们正在处理的是原始矩阵中的哪一列% 该函数有一个返回值，它返回正向化之后的指标，我们可以将其直接赋值给我们原始要处理的那一列向量enddisp('正向化后的矩阵 X =  ')disp(X)
end

正向矩阵标准化：

Z = X./repmat(sum(X.*X).^0.5,n,1);

计算得分并归一化：

D_P = sum([(Z - repmat(max(Z),n,1)).^2],2) ^ 0.5;
D_N = sum([(Z - repmat(min(Z),n,1)).^2],2) ^ 0.5;
S = D_N ./ (D_P + D_N);
Stand_S = S / sum(S);

还可以排一下序（降序排列，并保留索引）：

[sorted_S,index] = sort(stand_S,'descend')