本文主要是介绍用基于信息熵的topsis方法实现学生成绩的综合排名,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
TOPSIS方法排序的基本思路是首先定义决策问题的正理想解(即最好的)和负理想解(即最坏的),然后把实际可行解(样本)和正理想解与负理想解作比较。通过计算实际可行解与正理想解和负理想解的加权欧氏距离,得出实际可行解与正理想解的接近程度,以此作为排序的依据。若某个可行解(样本)最靠近理想解,同时又最远离负理想解,则此解排序最靠前。
通常,当排序时有多个指标需要考虑时,常用“专家打分法”来确定各个指标的权重,这容易造成评价结果可能由于人的主观因素而形成较大偏差。熵值法能较客观地反映数据本身信息的有序性,它通过评价指标值构成的判断矩阵来确定指标的权重,这样能尽量消除各因素权重的主观性,使评价结果更符合实际。
下面通过MATLAB实现基于信息熵的topsis方法,学习代码的同时也就弄清楚topsis方法的原理了:
%% 熵topsis方法的MATLAB实现,以“兰州大学数学与统计学院2015年应用统计硕士研究生复试分数”为例
%% 清空环境,导入数据
clear
clc
close all
% 兰州大学数学与统计学院2015年应用统计硕士研究生复试分数
% 成绩包括:初试总分X1、复试笔试成绩X2、复试专业面试成绩X3、复试外语笔试成绩X4、复试外语口语及听力测试成绩X5,共五个科目
% 原始排名计算方法:总分=(X1/5)*0.5+X2*0.2+(((X4+X5)/2)*0.2+X3*0.8)*0.3
load score
data=score(:,2:end);
%% 数据归一化处理
[n,m]=size(data);
maxdata=repmat(max(data),n,1);
mindata=repmat(min(data),n,1);
max_min=maxdata-mindata;
stddata=(data-mindata)./max_min;
%% 利用信息熵计算不同科目的权重
f=(1+stddata)./repmat(sum(1+stddata),n,1);
e=-1/log(n)*sum(f.*log(f));
d=1-e;
w=d/sum(d); % 权重向量
%% 计算加权决策矩阵,确定正理想解和负理想解
normdata=repmat(w,n,1).*stddata; % 加权决策矩阵
posideal=max(normdata); % 正理想解
negideal=min(normdata); % 负理想解
%% 计算加权后的决策数据与正负理想解的欧式距离
dtopos=sqrt(sum((normdata-repmat(posideal,n,1)).^2,2));
dtoneg=sqrt(sum((normdata-repmat(negideal,n,1)).^2,2));
%% 计算各样本与理想解得接近程度并得到排序结果
d=dtoneg./(dtoneg+dtopos);
[dscore,index]=sort(d,'descend');
%% 结果对比
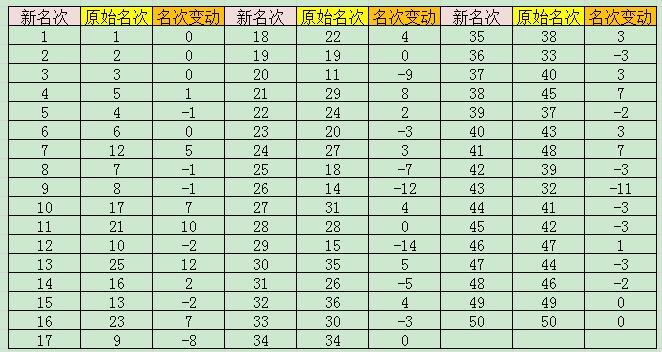
result=[{'新名次'},{'原名次'},{'名次变化'};num2cell(score(:,1)), num2cell(index),num2cell(index-score(:,1))]程序运行结果如下:
这篇关于用基于信息熵的topsis方法实现学生成绩的综合排名的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!