一个简单实用的评价模型——TOPSIS理想解法

​Hello！大家好，今天给大家介绍的是一个非常简单实用又好理解的评价模型——TOPSIS理想解法。本次案例的理论知识和数据均来自于《数学建模与数学实验》这本书，如果有想看该书的小伙伴，可在公众号中回复“《数学建模与数学实验》”（注意要打“《》”），即可获得该书的电子版，废话不多说，咱们直接进入正题。

TOPSIS原理

基本原理

（1）将n个评价指标看成n条坐标轴，由此可以构造出一个n维空间，则每个待评价的对象依照其各项指标的数据就对应n维空间中一个坐标点。
（2）针对各项指标从所有待评价对象中选出该指标的最优值（理想解，对应最优坐标点）和最差值（负理想解，对应最差坐标点），依次求出各个待评价对象的坐标点分别到最优坐标点和最差坐标点的距离d*和d0。

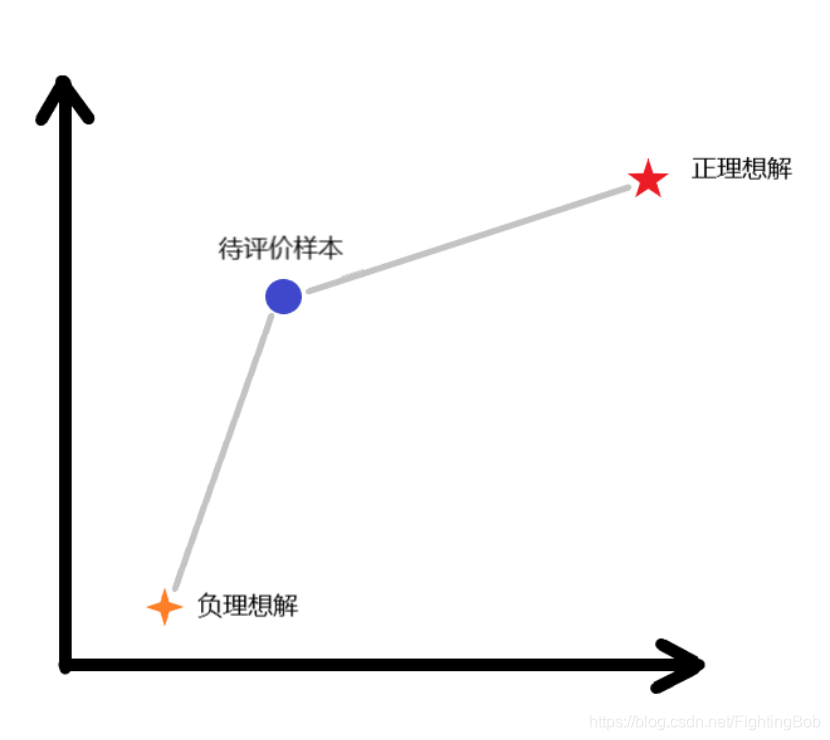
（3）构造评价参考值

则f值越大代表评价结果越优。

算法步骤

（1）构造决策矩阵A=(aij)m×n，每一列是一个评价指标，每一行是一条待评价样本；为去掉量纲效应，做规范化处理得到B=(bij)m×n，其中

注：该规范化法处理后，各评价样本的同一评价指标值的平方和为1，适合TOPSIS法中计算欧氏距离的场合。
（2）根据每个评价指标对评价结果的贡献程度的不同，指定不同的权重：w=[w1,…,wn]，将B的第j列乘以其权重wj，得到加权规范矩阵C=(cij)m×n。
（3）确定正理想解C*和负理想解C0：

其中，

（4）计算每个待评价样本到正理想解和负理想解的距离：


（5）计算每个待评价样本的评价参考值

再将fi从大到小排列，得到各评价样本的优劣结果。

在原书中，是以MATLAB进行实现，但当下Python当道，我们当然也要尝试用Python来实现看看！

Python代码实现

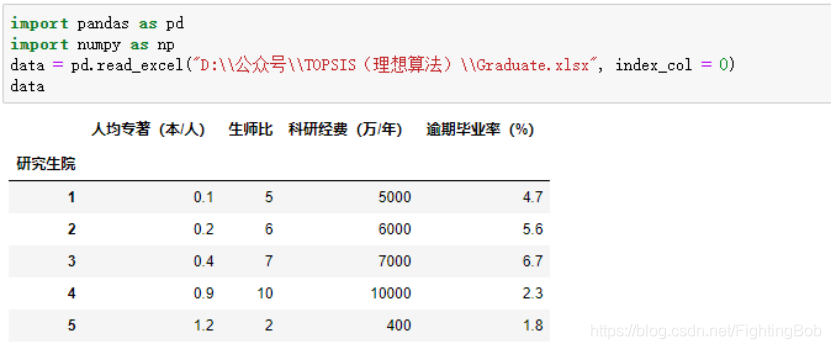
以下是五所研究生院的基本情况，我们要根据“人均专著”、“生师比”、“科研经费”、“逾期毕业率”四个方面来为这五所研究生院进行一个排名。

首先，先加载所需要的库，并读取数据：

import pandas as pd
import numpy as np
data = pd.read_excel("D:\\公众号\\TOPSIS（理想算法）\\Graduate.xlsx", index_col = 0)

然后，构建决策矩阵：

A = data.values

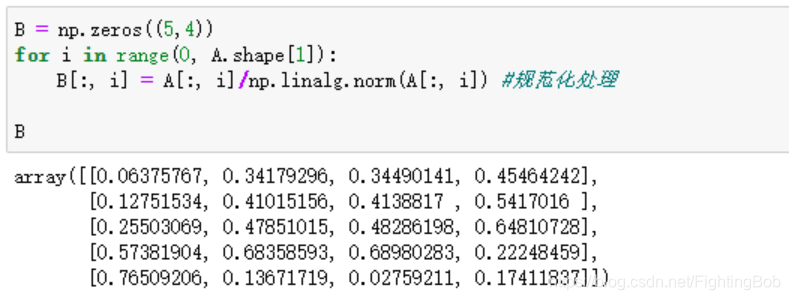
接着，对决策矩阵A进行规范化处理：

B = np.zeros((5,4))
for i in range(0, A.shape[1]):B[:, i] = A[:, i]/np.linalg.norm(A[:, i])

参数说明：
np.linalg.norm(x, ord=None, axis=None, keepdims=False)
1、x：表示矩阵（也可以是一维）；
2、ord：范数类型，默认值为None

3、axis：处理类型，默认值为None
axis=1表示按行向量处理，求多个行向量的范数
axis=0表示按列向量处理，求多个列向量的范数
axis=None表示矩阵范数
4、keepding：是否保持矩阵的二维特征，默认值为False
True表示保持矩阵的二维特性，False反之。

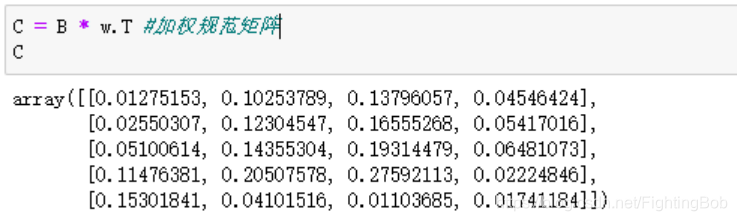
然后我们对四个维度设置相对应的权重，这里我们是根据2：3：4：1人为设定，当然也可以结合嫡值法进行定权：

w = np.array([0.2, 0.3, 0.4, 0.1])

C = B * w.T 

紧接着我们要求出正理想解和负理想解；
首先，先按列取最大值，求正理想解：

Cstar = C.max(axis=0)

但由于第四个指标是负向指标，即值越小越好，所以我们的正理想解的第四个指标应该取最小值：

Cstar[3] = C[:, 3].min()

同理，我们可求出负理想解：

C0 = C.min(axis=0) 
C0[3] = C[:, 3].max()

然后，就可以求各个样本到正负理想解的距离：

Sstar = np.zeros((1,5))
S0 = np.zeros((1,5))
for i in range(0, C.shape[0]):Sstar[:, i] = np.linalg.norm(C[i, :]-Cstar) S0[:, i] = np.linalg.norm(C[i, :]-C0)

再根据各样本到正负理想解的距离计算每个待评价样本的评价参考值：

f = S0/(S0 + Sstar)

最后，我们需要根据评价参考值，从大到小进行排序，展示出来即可：

ind = data.index.values
result = np.insert(f.T, 0, values = ind, axis = 1)
pd.DataFrame(result[np.lexsort(-result.T)], columns = ['对象', '得分'])

参数说明：
numpy.insert(arr, obj, values, axis)
1、arr：输入数组
2、obj：在其之前插入值的索引
3、values：要插入的值
4、axis：沿着它插入的轴，如果未提供，则输入数组会被展开

最后，我将以上的代码进行了整理，打包成了一个函数，以便大家使用，公众号中回复“TOPSIS”即可获得。

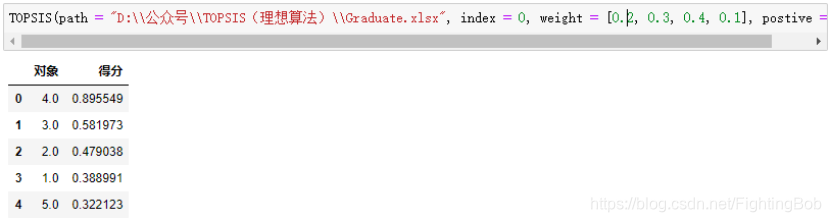
TOPSIS(path = "D:\\公众号\\TOPSIS（理想算法）\\Graduate.xlsx", index = 0, weight = [0.2, 0.3, 0.4, 0.1], postive = [3])

获得代码

以下是我的个人公众号，本文完整代码已上传，关注公众号回复“TOPSIS”，即可获得，回复“《数学建模与数学实验》”（注意要打“《》”），即可获得该书的电子版，谢谢大家支持。