TOPSIS优劣解距离法（自用）1

对于上一节，我们讲了AHP方法。但是层次分析法有一定的缺陷

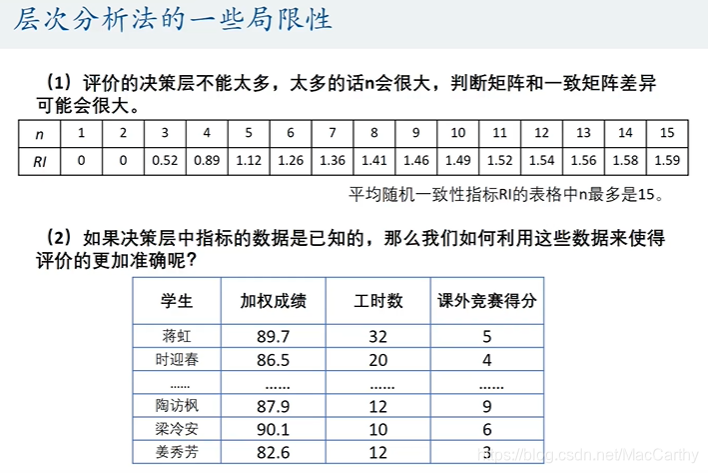
引例


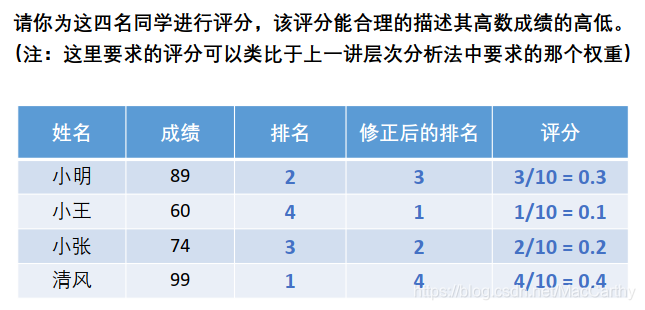
在这里我们看到，排名是越小越好。但是，我们是想打分，打分的话就是分数越大越好，所以我们为了合理地打分，就要对这个排名进行转化，怎么转化？
我们将原来的排名越小越好修正为越大越好。然后给出评分就是上图所示。

但是，我们的上面这个方法有不合理之处。比如，如果小王和清风考得是另一个成绩，但是他们的名次就还是没有发生改变，这时候，这种方法就不能全部的完全的反映表格中的信息了。
用数学语言来描述就是——虽然他们有相关性，但是相关性不是很强。

怎么尽量使其有较强的相关性呢？为了更容易的计算，我们要对分数进行修正。

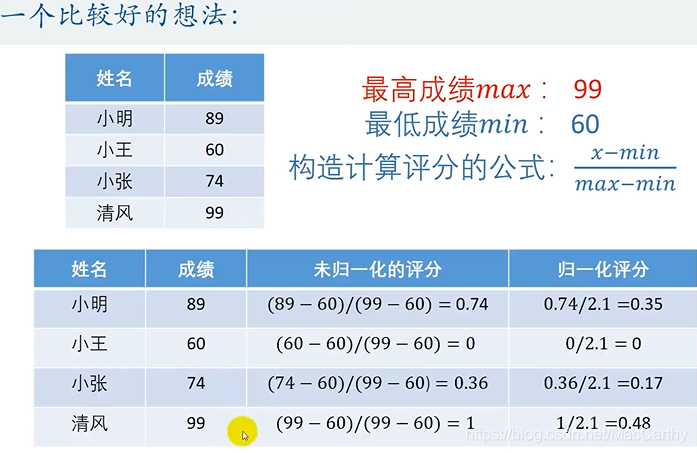
用最大最最小值法。把他们都修正控制在了0-1之间。
怎么进行打分呢？
归一化——修正后的分数/该列的和。
归一化后就发现得分相加是1了。

问题拓展——增加指标个数

在上一个图中，有两个指标。分别为极大型指标和极小型指标，这两个指标分别代表越大越好和越小越好。这时候你就不能把他俩放在一起评价了，因为他们的方向是不同的。所以你就要同一方向，怎么统一？——指标正向化

解释一下最下面的极大型和极小型。成绩肯定是越高越好，所以就是极大型指标；与他人争吵的次数，肯定是越小越好，所以是极小型指标；
我们要进行指标正向化，就是把所有的指标都转化为极大型指标，那么就要用与他人争吵的次数这一列中的 max-x 便成功完成指标的正向化。
转化后的“吵架次数指标”就变成了极大型指标，就变成了指标越大越好了。

正向化后怎么办？
你不能直接就把这两个指标简单粗暴的加起来，因为他们的单位不同。所以，你就要进行标准化处理，来消除量纲的影响。



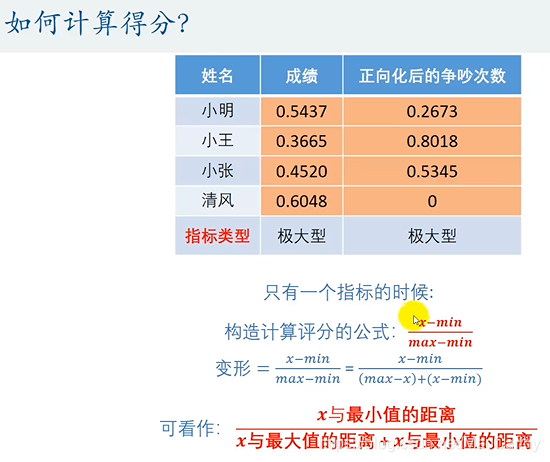
回到刚才打分的问题：

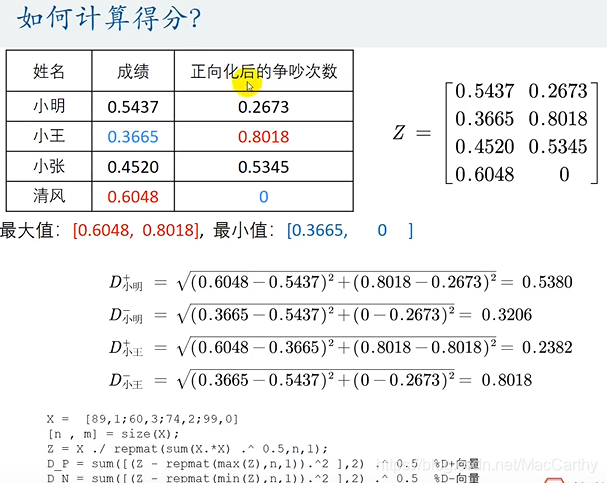
总结：TOPSIS方法步骤






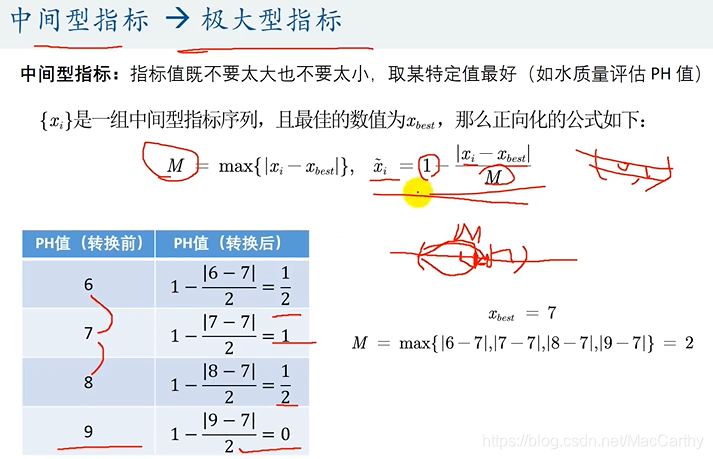
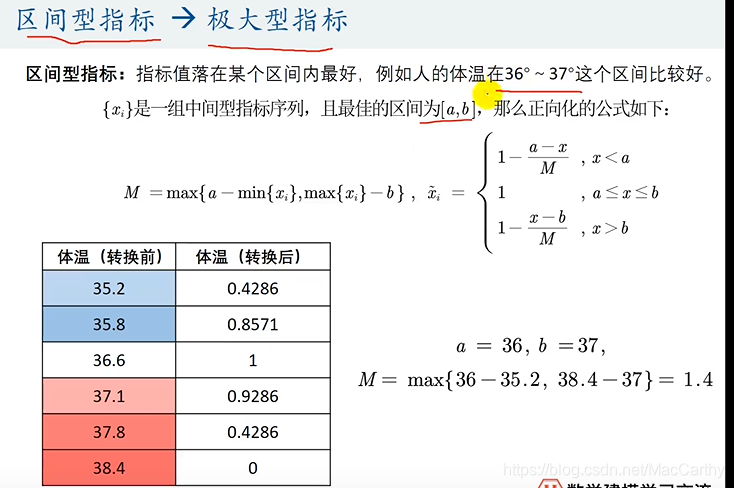
计算指标得分后不要忘了归一化得分。