【评价类模型】Topsis法（优劣解距离法）

【评价类模型】Topsis法（优劣解距离法）

学习前言

Topsis法解决问题三步曲：

       第一步：将原始矩阵正向化

              最常见的四种指标：

              极小型指标转换为极大型指标：

              中间型指标转换为极大型指标：

              区间型指标转换为极大型指标： 

        第二步：正向化后的矩阵标准化

        第三步：计算得分并归一化

             核心公式：

             公式解释：

             总结：

牛刀小试：

学习前言

        Topsis是一个非常有趣的评价类模型，该模型是远优于层次分析法的，强烈推荐食用。抱着“若无必要，勿添新知”的想法，下面解决问题的过程博主尽量不引入没有必要的知识点，但都会在最后补充完整！

Topsis法解决问题三步曲：

        第一步：将原始矩阵正向化

                  这一步是用来统一指标类型的，将所有的指标转化为极大型指标称为指标正向化。

最常见的四种指标：

极小型指标转换为极大型指标：

                极小型指标转换为极大型指标的公式很简单，即：max -  x，如果所有元素均为正数，那么也可以用 1 / x 。  

中间型指标转换为极大型指标：

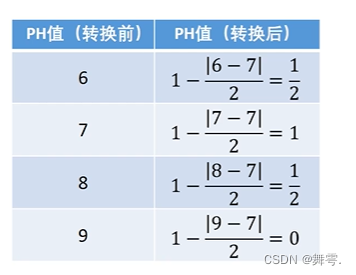
            中间型指标转换为极大型指标的公式稍微复杂了一点点：

区间型指标转换为极大型指标： 

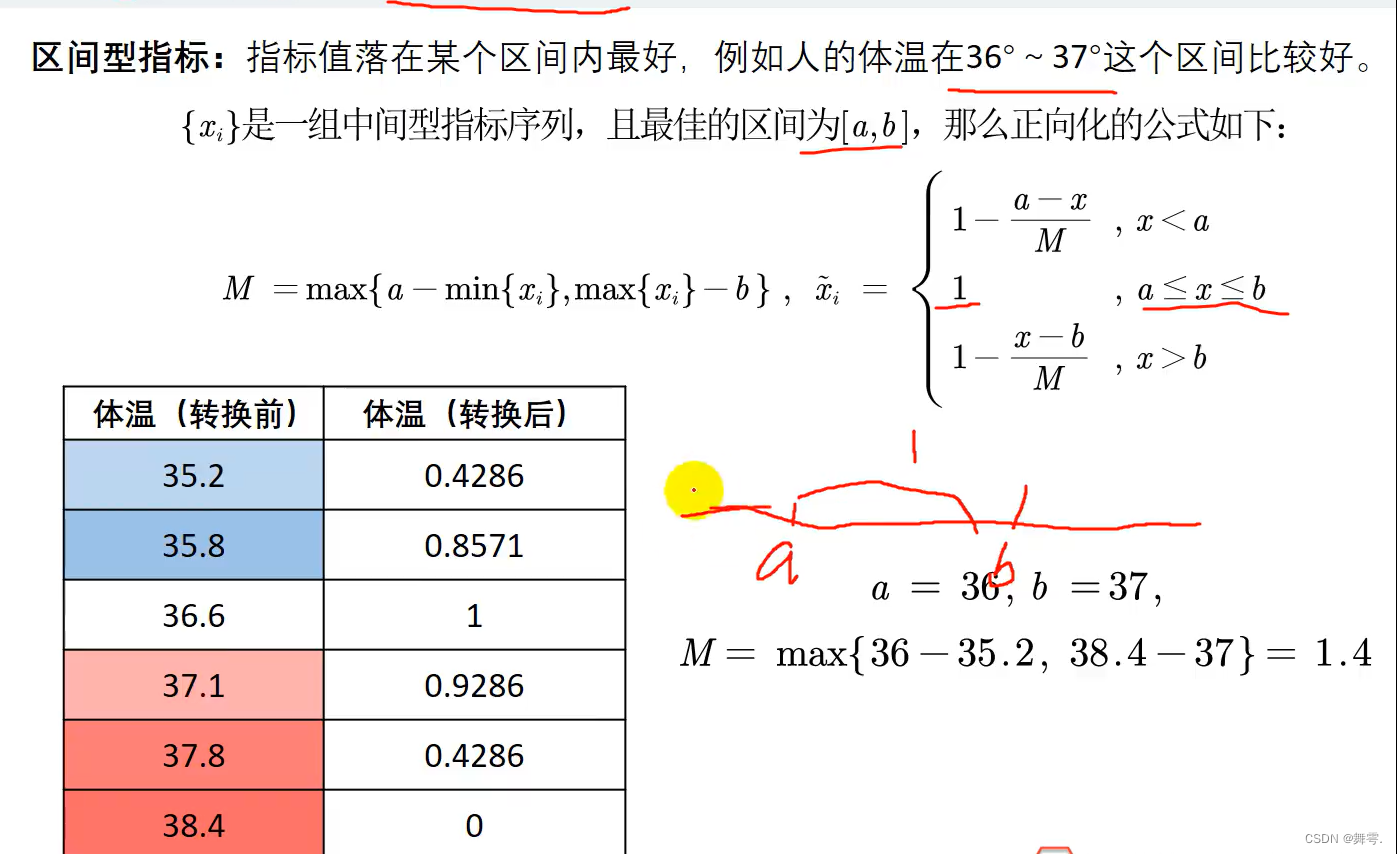
        第二步：正向化后的矩阵标准化

                标准化的目的就是消除不同指标量纲的影响。

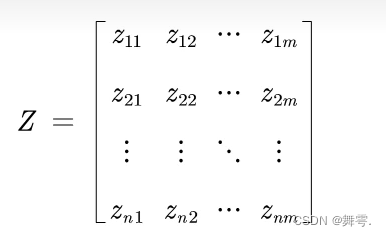
                假设有n个要评价的对象，m个评价指标（已经正向化了）构成的正向化矩阵如下：

                        那么，对其标准化的矩阵标记为Z，Z中的每一个元素：

        第三步：计算得分并归一化

             核心公式：

                   即：

            当看到这里，想必大家已经明白了优劣解距离法这个名词的由来，什么是优解？就是x与最大值的距离，劣解反之。

              公式解释：

            假设有n个要评价的对象，m个评价指标的标准化矩阵：

        总结：

牛刀小试：

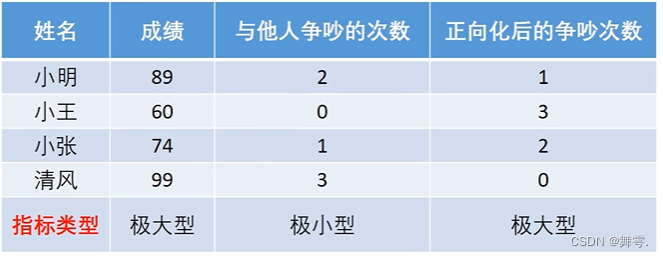
        题目： 请您为四名同学进行评分。

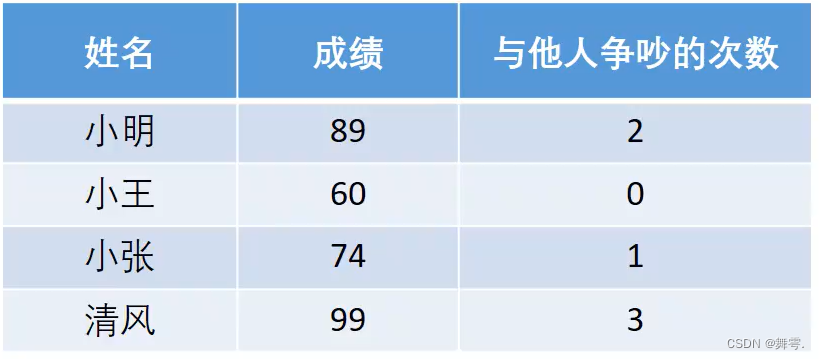
        小case：在上述问题中， 对于成绩这个指标自然是越大越好，这样子的指标我们叫做极大型指标。另外的，与他人争吵的次数这个指标就叫做极小型指标。

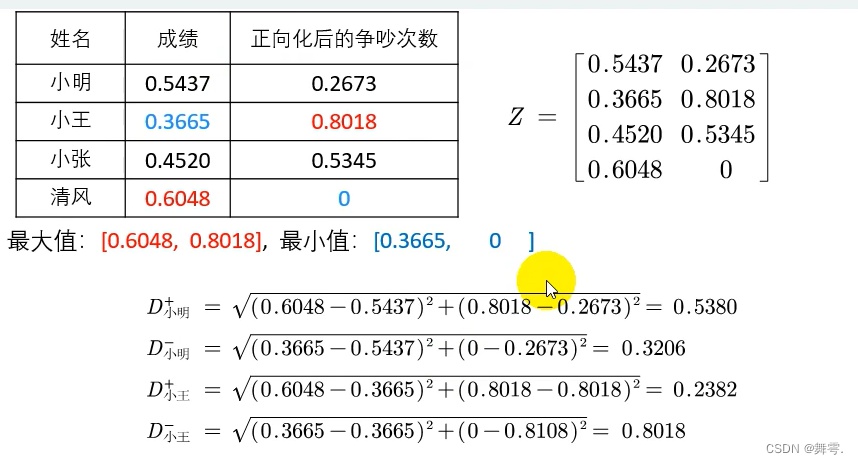
        1、将极小型指标转化为极大型指标得到正向化矩阵；

        2、将正向化矩阵标准化；

        3、通过公式计算得分。

结果：