【建模算法】TOPSIS法（Python实现）

【建模算法】TOPSIS法（Python实现）

Topsis法，全称为Technique for Order Preference by Similarity to an Ideal Solution，中文常翻译为“优劣解距离法”或“逼近理想解排序法”，该方法是一种通过比较样本值与理想值的距离实现综合评价的方法。能够根据现有的数据，对个体进行评价排序。TOPSIS算法是直接用来评价的，它也可以和赋权方法一起使用。

逼近理想解排序法（TOPSIS），采用相对接近度来表征各个评价对象与参考点的距离。首先在空间确定出参考点，包括最优和最劣点，然后计算各个评价对象与参考点的距离，与最优点越近或与最劣点越远说明被评价对象的综合特性越好。

一、问题描述

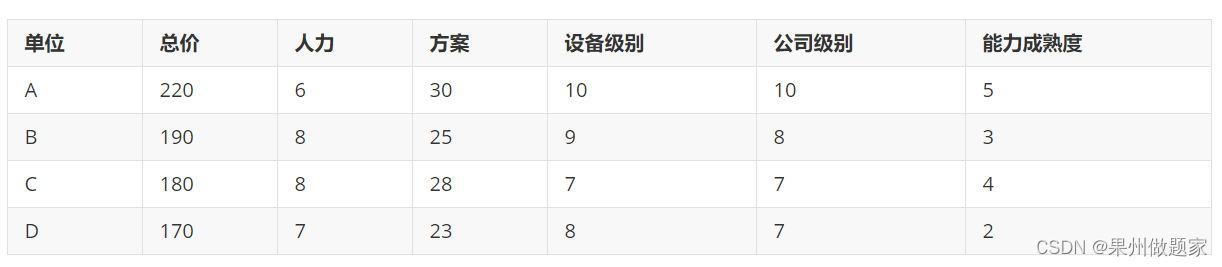
现需要对投标者进行综合评价，实现某招标公司的招标项目决策。现有A、B、C、D四个投标者，招标公司对它们的总价、人力、方案、设备级别、公司级别、能力成熟度分别进行评价，觉得哪个投标者应该中标？投标单位的各项指标数量与分值如下：

二、TOPSIS法评价步骤

step0：指标正向化

不同的指标代表含义不一样，有的指标越大越好，称为越大越优型指标。有的指标越小越好，称为越小越优型指标，而有些指标在某个点是最好的，称为某点最优型指标。为方便评价，应把所有指标转化成越大越优型指标。

设有m个待评对象，n个评价指标，可以构成数据矩阵$X=(x_{ij}{)}_{m\times n}$ ， 设数据矩阵内元素，经过指标正向化处理过后的元素为 $x_{ij}^{\prime }$

• 越小越优型指标：

$$x_{ij}^{\prime }=max(x_{ij})-x_{ij}$$

其他处理方法也可，只要指标性质不变即可

• 某点最优型指标：

  设最优点为a, 当a=90时E最优。
  

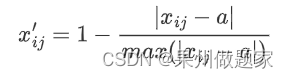
​ 其他处理方法也可，只要指标性质不变即可

• 越大越优型指标：

$$x_{ij}^{\prime }=x_{ij}$$

此类指标可以不用处理，想要处理也可，只要指标性质不变

step1：数据标准化

因为本案例数据指标都是正向指标，不需要进行指标正向化，若有其他性质指标应把它们都正向化。

本案例直接进入数据标准化，每个指标的数量级不一样，需要把它们化到同一个范围内比较。可以用最大最小值标准化方法。本案例使用另一方法。

设有m个待评对象，n个评价指标，可以构成数据矩阵$X=(x_{ij}{)}_{m\times n}$ ，设数据矩阵内元素$x_{ij}$，标准化处理过后的元素为$x_{ij}^{\prime }$
$$x_{ij}^{\prime }=\frac{x_{ij}}{\sqrt{{\sum }_{i=1}^m{x}_{ij}^2}}$$

step2：计算加权后的矩阵

之前有讲过层次分析法、熵权法、变异系数法，都是获取权重的方法，可以翻看之前的文章。现设得到指标的权重为$w_i$ ，加权重后的数据为$r_{ij}$

每个指标的数量级不一样，需要把它们化到同一个范围内比较。上一篇建模算法用到了最大最小值标准化方法。此篇可以用一个新的标准化方法，处理如下：

设标准化后的数据矩阵元素为$r_{ij}$ ,由上可得指标正向化后数据矩阵元素为$x_{ij}^{\prime }$
$$r_{ij}=w_j{x}_{ij}^{\prime }$$

step3：计算矩阵和最值之间的距离

处理过后可以构成数据矩阵$R=(r_{ij}{)}_{m\times n}$

• 定义每个指标即每列的最大值为$r_j^{+}$
  $$r_j^{+}=max(r_{1j},r_{2j},...,r_{nj})$$

• 定义每个指标即每列的最小值为$r_j^{-}$
  $$r_j^{-}=min(r_{1j},r_{2j},...,r_{nj})$$
  ​

• 定义第i个对象与最大值距离为$d_i^{+}$
  $$d_i^{+}=\sqrt{\sum _{j=1}^n(r_j^{+}-r_{ij}{)}^2}$$

• 定义第i个对象与最小值距离为$d_i^{-}$
  $$d_i^{-}=\sqrt{\sum _{j=1}^n(r_j^{-}-r_{ij}{)}^2}$$

step4：计算评分

得分为：
$$Scor{e}_i=\frac{d_i^{-}}{d_i^{+}+d_i^{-}}$$
明显可以看出$0\le Scor{e}_i\le 1$ ，当$Scor{e}_i$越大时，

$d_i^{+}$越小，说明指标离最大值距离越小，越接近最大值。

三、求解结果

结果如下：

四、实现代码

Python源码：

import pandas as pd
import numpy as np#读取数据
data=pd.read_excel('投标单位各项指标和分值.xlsx')#数据标准化
label_need=data.keys()[1:]
data1=data[label_need].values
[m,n]=data1.shape
data2=data1.copy().astype('float')
for j in range(0,n):data2[:,j]=data1[:,j]/np.sqrt(sum(np.square(data1[:,j])))#计算加权重后的数据
w=[0.3724, 0.1003,0.1991, 0.1991,0.0998,0.0485]   #使用求权重的方法求得,参见文献1
R=data2*w#计算最大最小值距离
r_max=np.max(R,axis=0)   #每个指标的最大值
r_min=np.min(R,axis=0)   #每个指标的最小值
d_z = np.sqrt(np.sum(np.square((R -np.tile(r_max,(m,1)))),axis=1))  #d+向量
d_f = np.sqrt(np.sum(np.square((R -np.tile(r_min,(m,1)))),axis=1))  #d-向量  #计算得分
s=d_f/(d_z+d_f )
Score=100*s/max(s)
for i in range(0,len(Score)):print(f"第{i+1}个投标者百分制得分为：{Score[i]}") 

参考文献：

【1】陈雷,王延章.基于熵权系数与TOPSIS集成评价决策方法的研究[J].控制与决策,2003(04):456-459.