评价模型：TOPSIS法（理想解法）

写在前面：

博主本人大学期间参加数学建模竞赛十多余次，获奖等级均在二等奖以上。为了让更多学生在数学建模这条路上少走弯路，故将数学建模常用数学模型算法汇聚于此专栏，希望能够对要参加数学建模比赛的同学们有所帮助。

目录

1.算法介绍

2.算法步骤

（1）用向量规范化的方法求得规范决策矩阵 

（2）构造加权规范阵

（3）确定正理想解和负理想解

（4）计算各方案到正理想解与负理想解的距离 

（5）计算各方案的综合评价指数 

（6）将由大到小进行排序 

3.案例分析

 3.1模型建立与求解

（1）对属性进行向量规范化

（2） 计算加权的向量规范化属性矩阵

 （3）求出各属性的正理想解和负理想解

 （4）求出各方案到正理想解和负理想解的距离

（5）计算各方案的排序指标值并从优到劣进行排序

3.2 结果分析

---

1.算法介绍

TOPSIS法也称为理想解法，是一种有效的多指标评价方法。这种方法通过构造评价问题的正理想解和负理想解及各指标的最优解和最劣解，通过计算每个方案到理想方案的相对贴近度，即靠近正理想解和远离负理想解的程度，来对方案进行排序，从而选出最优方案。

2.算法步骤

（1）用向量规范化的方法求得规范决策矩阵 

设原问题的决策矩阵，规范化后的决策矩阵为，其中

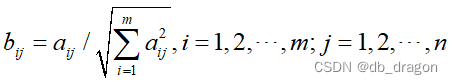
其中m为矩阵数据的行数，n为矩阵数据的列数。

（2）构造加权规范阵

设各属性的权重为wij，则 

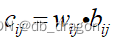
（3）确定正理想解和负理想解

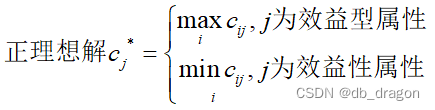
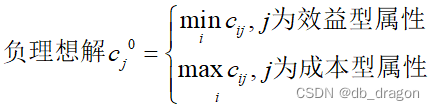
（4）计算各方案到正理想解与负理想解的距离 

 备选方案到正理想解的距离为

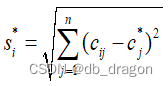
备选方案到负理想解的距离

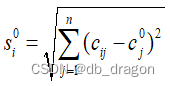
（5）计算各方案的综合评价指数 

（6）将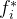由大到小进行排序 

3.案例分析

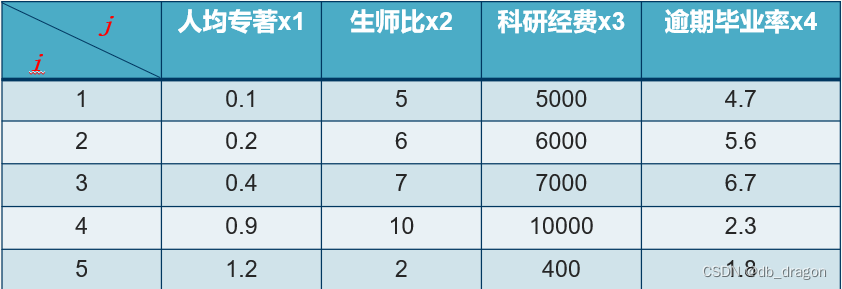
        为了客观的评价我国研究生教育的实际状况和各研究生院的教学质量，国务院学位委员会办公室组织过一次研究生院的评估，为了取得经验，先选5所研究生院，收集有关数据资料进行了试评估，表中是所给出的部分数据。

 3.1模型建立与求解

（1）对属性进行向量规范化

对生师比进行区间型属性变换：设给定的最优区间为，为无法容忍下限，为无法容忍上限，则

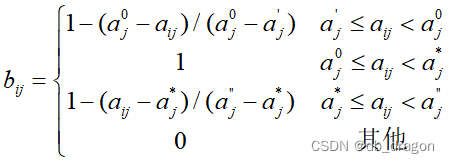
设研究生院的生师比的最优区间为[5,6]，下限为2，上限为12，对生师比进行规范化处理得到的结果如下： 

处理前	处理后
5	1
6	1
7	0.8333
10	0.3333
2	0

clc,clear
x2=@(qujian,lb,ub,x)(1-(qujian(1)-x)./(qujian(1)-lb)).*(x>=lb&x<qujian(1))+...
(x>=qujian(1)&x<=qujian(2))+(1-(x-qujian(2))./(ub-qujian(2))).*(x>qujian(2)&x<=ub);
qujian=[5,6];lb=2;ub=12;
ssb=[5 6 7 10 2]';
ssb2=x2(qujian,lb,ub,ssb)

对人均专著、科研经费、逾期毕业率进行向量规范化处理，得到如下结果： 

人均专著   生师比     科研经费   逾期毕业率  

    0.0638    0.5970    0.3449    0.4546

    0.1275    0.5970    0.4139    0.5417

    0.2550    0.4975    0.4829    0.6481

    0.5738    0.1990    0.6898    0.2225

    0.7651         0        0.0276    0.1741

（2） 计算加权的向量规范化属性矩阵

 设置权向量w=[0.2,0.3,0.4,0.1],得到加权的向量规范化属性矩阵如下：

人均专著   生师比     科研经费   逾期毕业率  

    0.0128    0.1791    0.1380      0.0455

    0.0255    0.1791    0.1656      0.0542

    0.0510    0.1493    0.1931      0.0648

    0.1148    0.0597    0.2759      0.0222

    0.1530         0        0.0110      0.0174

 （3）求出各属性的正理想解和负理想解

正理想解：Cstar = 1×4   

    0.1530    0.1791    0.2759    0.0174

负理想解：C0 = 1×4   

    0.0128         0    0.0110    0.0648

 （4）求出各方案到正理想解和负理想解的距离

各方案到正理想解的距离

Sstar = 1×5   

    0.1987    0.1726    0.1428    0.1255    0.3198

各方案到负理想解的距离

S0 = 1×5   

    0.2204    0.2371    0.2385    0.2932    0.1481

（5）计算各方案的排序指标值并从优到劣进行排序

f = 1×5   

    0.5258    0.5787    0.6255    0.7003    0.3165

ind = 1×5   

     4     3     2     1     5

3.2 结果分析

根据求解结果可知：

1~5号研究生院教学质量的得分分别是0.5258，0.5787，0.6255，0.7003，0.3165

得分排名依次为4 3 2 1 5

Matlab代码：

clc,clear
a=[0.1 5 5000 4.7
0.2 6 6000 5.6
0.4 7 7000 6.7
0.9 10 10000 2.3
1.2 2 400 1.8];
[m,n]=size(a);
x2=@(qujian,lb,ub,x)(1-(qujian(1)-x)./(qujian(1)-lb)).*(x>=lb&x<qujian(1))+...
(x>=qujian(1)&x<=qujian(2))+(1-(x-qujian(2))./(ub-qujian(2))).*(x>qujian(2)&x<=ub);
qujian=[5,6];lb=2;ub=12;
a(:,2)=x2(qujian,lb,ub,a(:,2));
for j=1:n
b(:,j)=a(:,j)/norm(a(:,j))%向量规范化
end
w=[0.2 0.3 0.4 0.1];
c=b.*repmat(w,m,1)
Cstar=max(c);%正理想解
Cstar(4)=min(c(:,4))
C0=min(c);%负理想解
C0(4)=max(c(:,4))
for i=1:m
Sstar(i)=norm(c(i,:)-Cstar);%求到正理想解的距离
S0(i)=norm(c(i,:)-C0);%求到负理想解的距离
end
Sstar,S0
f=S0./(Sstar+S0)
[sf,ind]=sort(f,'descend')

---

TOPSIS搭配熵权法会更好用哦！