本文主要是介绍数学建模(二)、TOPSIS法(优劣解距离法),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
TOPSIS 法(优劣解距离法)
- 1、什么是 TOPSIS 法(优劣解距离法)?
- 2、解法步骤
- 统一指标类型
- 标准化处理(消除不同指标量纲的影响)
- 通过标准化矩阵计算评分
1、什么是TOPSIS法(优劣解距离法)?
TOPSIS 法是一种理想目标相似性的顺序选优技术,在多目标决策分析中是一种非常有效的方法。它通过归一化后的数据规范化矩阵,找出多个目标中最优目标和最劣目标 (分别用理想解和反理想解表示) , 分别计算各评价目标与理想解和反理想解的距离,获得各目标与理想解的贴近度,按理想解贴近度的大小排序,以此作为评价目标优劣的依据。贴近度取值在 0~1 之间,该值愈接近 1, 表示相应的评价目标越接近最优水平;反之,该值愈接近 0, 表示评价目标越接近最劣水平。
2、解法步骤
统一指标类型
常见的四种指标
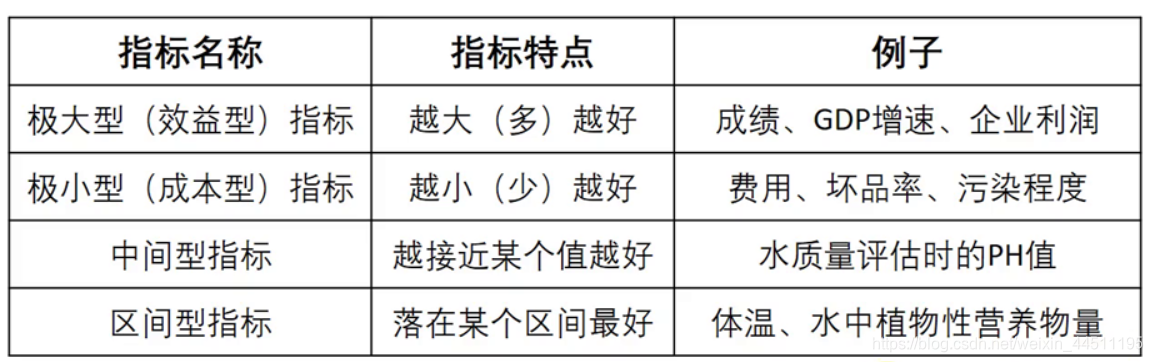
将所有指标转化位极大型称为指标正向化(最常用)
-
极小型指标转换为极大型指标:
1、公式: m a x − x max-x max−x
2、如果所有的元素均为正数,那么也可以使用 1 / x 1/x 1/x -
中间型指标转换为极大型指标: M = m a x { ∣ x i − x b e s t ∣ } , x z = 1 − ( ∣ x i − x b e s t ∣ / M ) M=max\left \{ |x_{i}-x_{best}|\right \},x_{z}=1-(|x_{i}-x_{best}|/M) M=max{∣xi−xbest∣},xz=1−(∣xi−xbest∣/M)

- 区间型指标转换为极大型指标:

标准化处理(消除不同指标量纲的影响)
假设有n个需要评价的对象,m个评价指标(全部正向化)构成的正向化矩阵:


通过逐一计算出zij的数值可以列出标准化矩阵Z
通过标准化矩阵计算评分
在标准化矩阵Z中

找出最大值 Z+
Z + = ( Z 1 + , Z 2 + , . . . , Z m + ) Z^{+}=(Z_{1}^{+},Z_{2}^{+},...,Z_{m}^{+}) Z+=(Z1+,Z2+,...,Zm+)
其中每一个元素为标准化矩阵中该元素所在列的最大值:
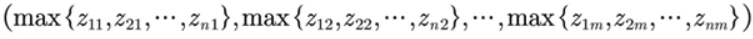
找出最小值 Z-
Z − = ( Z 1 − , Z 2 − , . . . , Z m − ) Z^{-}=(Z_{1}^{-},Z_{2}^{-},...,Z_{m}^{-}) Z−=(Z1−,Z2−,...,Zm−)
其中每一个元素为标准化矩阵中该元素所在列的最小值:
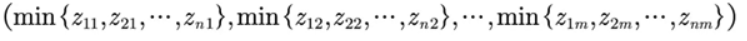
计算出评价对象与最大 / 小值的的距离
最后进行归一化处理
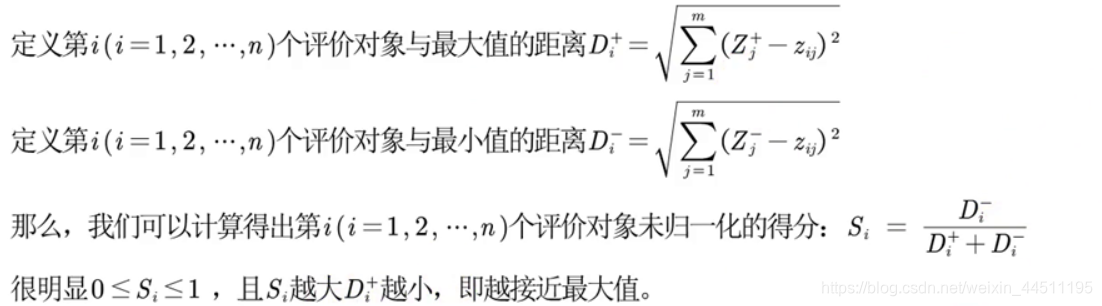
最后得到的S越大则代表目标越优
这篇关于数学建模(二)、TOPSIS法(优劣解距离法)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








