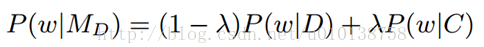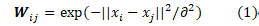拉普拉斯专题
Open3D mesh 拉普拉斯laplacian滤波
目录 一、概述 1.1原理 1.2实现步骤 1.3应用场景 二、代码实现 2.1关键函数 参数详解 返回值 2.2完整代码 三、实现效果 3.1加入噪点的mesh 3.2迭代10次 3.3迭代100次 Open3D点云算法汇总及实战案例汇总的目录地址: Open3D点云算法与点云深度学习案例汇总(长期更新)-CSDN博客 一、概述 拉普
拉普拉斯算子从笛卡尔坐标系到圆柱坐标系下的推导过程
这段时间推导圆膜振动方程的时候,需要将振动方程从笛卡尔坐标系转换到圆柱坐标系。虽然这个结果书上都有了,但是不满足于直接给出的结果,想自己推导一下。于是就有了下面的内容。总结起来:就是将笛卡尔坐标系下的拉普拉斯算子定义式和圆柱坐标系下拉普拉斯算子定义式之间的关系通过坐标转换对应起来,然后利用待定系数法求解相应的系数就可以了。话不多说,上干货。 笛卡尔坐标系下的拉普拉斯算子定义为: (2-1)
电路笔记(PCB):数字滤波电路的拉普拉斯变换与零极点分析
拉普拉斯变换基础 拉普拉斯变换 拉普拉斯变换是一种积分变换,用于将一个时间域的函数(通常是信号或系统的响应)转换为一个复频域的函数。这种变换可以简化许多微分方程和线性系统分析的过程。其定义为: L { f ( t ) } = F ( s ) = ∫ 0 ∞ f ( t ) e − s t d t \mathcal{L}\{f(t)\} = F(s) = \int_{0}^{\infty} f
边缘检测(梯度和拉普拉斯比较)
1.概述 边缘检测是图像处理和计算机视觉中的基本问题,边缘检测的目的是标识数字图像中亮度变化明显的点。图像属性中的显著变化通常反映了属性的重要事件和变化。 这些包括(i)深度上的不连续、(ii)表面方向不连续、(iii)物质属性变化和(iv)场景照明变化。 边缘检测是图像处理和计算机视觉中,尤其是特征提取中的一个研究领域。 图像边缘检测大幅度地减少了数据量,并且剔除
证:单位冲激函数(连续)和单位脉冲函数(离散)的拉普拉斯/Z变换 皆为 “1”
输入信号 ( x(t) = \delta(t) ) 的拉普拉斯变换为 ( X(s) = 1 ) 是因为单位冲激函数 (\delta(t)) 的拉普拉斯变换有一个特殊且重要的性质。【在离散时间系统中,拉普拉斯变换的离散对应物是Z变换。】 单位冲激函数 (\delta(t)) 的定义 单位冲激函数(Dirac Delta 函数) (\delta(t)) 的定义是: (\delta(t)) 在 (
四种信号在时域和频域之间的对应关系(连续周期/非周期、离散周期/非周期)(拉普拉斯、Z变换)
1. 连续周期时间信号 时域:连续周期时间信号可以理解为一种在时间上重复的波形,比如正弦波或余弦波。频域:在频域中,这种信号可以分解为一系列不同频率的正弦波的叠加。每个正弦波对应一个频率和一个复数系数 (C_n),这些系数告诉我们各个频率成分的强度和相位。 公式解释: x ~ ( t ) = ∑ n = − ∞ ∞ C n ⋅ e j n ω 0 t \tilde{x}(t) = \
2-1基于matlab的拉普拉斯金字塔图像融合算法
基于matlab的拉普拉斯金字塔图像融合算法,可以使部分图像模糊的图片清楚,也可以使图像增强。程序已调通,可直接运行。 2-1 图像融合 拉普拉斯金字塔图像融合 - 小红书 (xiaohongshu.com)
python实现opencv学习十五:高斯金字塔和拉普拉斯金字塔
要求:拉普拉斯金字塔时,图像大小必须是2的n次方*2的n次方,不然会报错 代码如下: # -*- coding=GBK -*-import cv2 as cv#高斯金字塔def pyramid_image(image):level = 3#金字塔的层数temp = image.copy()#拷贝图像pyramid_images = []for i in range(level):dst
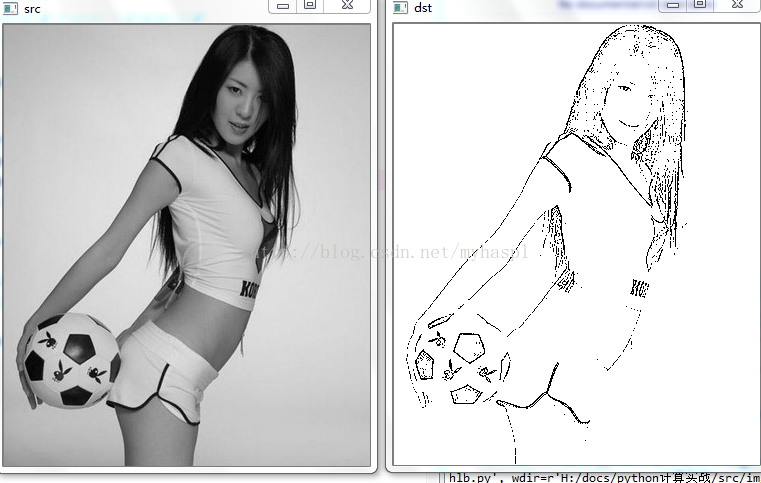
数学之路-python计算实战(21)-机器视觉-拉普拉斯线性滤波
拉普拉斯线性滤波,.边缘检测 Laplacian Calculates the Laplacian of an image. C++: void Laplacian (InputArray src, OutputArray dst, int ddepth, int ksize=1, double scale=1, double delta=0, int bor
数学之路-python计算实战(20)-机器视觉-拉普拉斯算子卷积滤波
拉普拉斯算子进行二维卷积计算,线性锐化滤波 # -*- coding: utf-8 -*- #线性锐化滤波-拉普拉斯算子进行二维卷积计算#code:myhaspl@myhaspl.comimport cv2import numpy as npfrom scipy import signalfn="test6.jpg"myimg=cv2.
狄里克雷平滑(Dirichlet)、线性插值平滑(Linear Interpolated)、拉普拉斯平滑(Laplacian)
一元语言模型(Unigram Language Model)就是关于全部单词上的一个概率分布,它认为每篇文章都对应一个一元语言模型,文章中的单词都是从这个概率分布中采样得到。所以计算文章和查询语句之间的相关性,相当于计算文章对应的一元语言模型产生出查询语句的概率。 通常我们统计文档中的单词频率分布来估计文章对应的一元语言模型,但是未出现在文档中的单词的概率就被设置为0了,这显然是不合理的。所以需
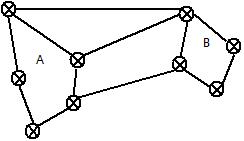
graph Laplacian 拉普拉斯矩阵
拉普拉斯矩阵是个非常巧妙的东西,它是描述图的一种矩阵,在降维,分类,聚类等机器学习的领域有很广泛的应用。 什么是拉普拉斯矩阵 拉普拉斯矩阵 先说一下什么是拉普拉斯矩阵,英文名为Laplacian matrix,其具体形式得先从图说起,假设有个无向图如下所示, 其各个点之间的都有相应的边连接,我们用某个指标(这地方可以任意选择,比如欧氏距离、测地距离、或
拉普拉斯IPO:以知识产权转化运用促进高质量发展!
2024年全国知识产权宣传周活动在今年4月20日至26日开展。自2009开始,知识产权宣传周已历时十余年,从发展到运用到保护,知识产权强国建设的步伐一步也没有停下。今年宣传周的活动主题是:“知识产权转化运用促进高质量发展”。 创新是引领发展的第一动力,保护知识产权就是保护创新。在发挥法治保障作用,将知识产权有效转化为现实生产力,推动产业转型升级,促进经济社会高质量发展的道路上,除却政策的引领下,
傅立叶变换与拉普拉斯变换的区别与联系?
傅里叶变换和拉普拉斯变换都是信号处理中的重要工具,它们有以下几个主要区别: 定义域:傅里叶变换是在频率域(即虚轴)上定义的,而拉普拉斯变换在复平面上的特定区域内定义。 适用范围:傅里叶变换主要用于分析周期信号、非周期信号以及能量有限的信号。拉普拉斯变换的适用范围更广,可以处理不稳定的、因果的以及非因果的信号。 收敛性:傅里叶变换要求信号在时域内绝对可积,这限制了它的适用范围。拉普拉斯变换通过引入
拉普拉斯IPO丨用创新科技助力中国光伏产业高质量发展
近年来,在“以科技创新引领现代化产业体系建设”的战略指引下,整个光伏行业持续推动技术迭代与生产力升级,朝着更高光电转化效率、更低成本加速迈进。 在此背景下,一批以技术驱动为第一生产力的光伏厂商们,在自身领域中不断追求创新,为行业的技术突破贡献力量。 异军突起背后 当前,中国光伏行业已经实现全球领跑,电池片、组件等重点环节产量产能的全球占比均达80%以上。其中,中国的组件产量和累计装机量更是连
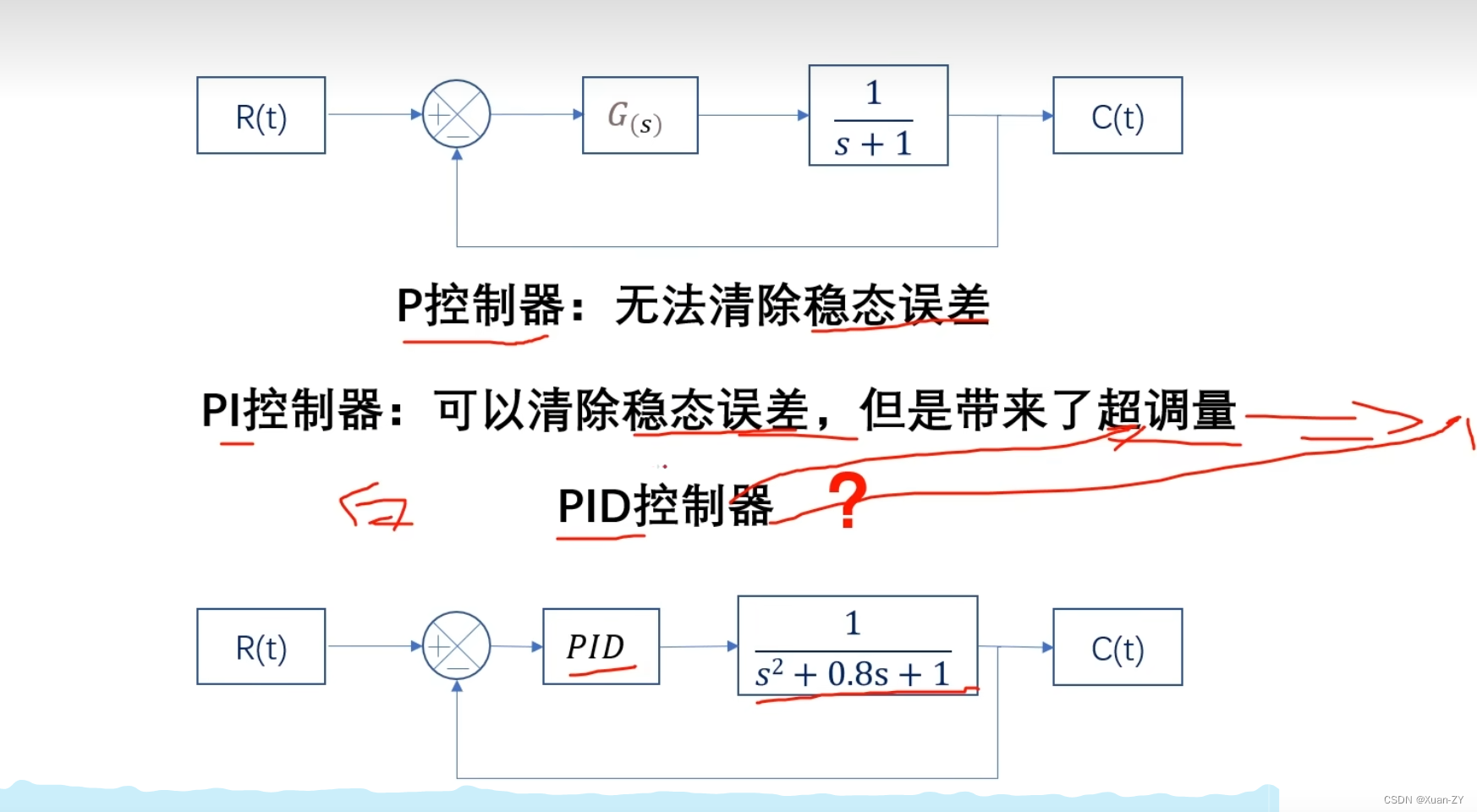
【电控笔记4】拉普拉斯-传递函数-pid
数据标幺化 拉普拉斯变换 欧拉公式 常见s变换 s变换性质 pid分析 p控制,存在稳态误差 可以求出p的取值范围p>-1,否则发散 pi消除稳态误差 把kp换成Gs 只用pi控制,不加微分的原因: 微分之后,噪声增大高频噪声频率的倍数 总结 遗留问题 s+1分之1,一阶惯性环节是电机模型吗?
【图像融合】基于matlab GUI拉普拉斯金字塔+小波变换+NSCT图像融合【含Matlab源码 870期】
✅博主简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,Matlab项目合作可私信。 🍎个人主页:海神之光 🏆代码获取方式: 海神之光Matlab王者学习之路—代码获取方式 ⛳️座右铭:行百里者,半于九十。 更多Matlab仿真内容点击👇 Matlab图像处理(进阶版) 路径规划(Matlab) 神经网络预测与分类(Matlab) 优化求解(Matlab) 语音处理(Matlab
【图像融合】基于matlab GUI高斯金字塔+拉普拉斯金字塔彩色图像融合【含Matlab源码 1506期】
一、区域分割图像融合简介 图像的分解 对源图像进行融合时,首先对图像进行分解,利用拉普拉斯金字塔分解,先对图像进行高斯金字塔分解,然后再进行拉普拉斯金字塔分解。 1 高斯金字塔分解 记源图像为G0,G0即为高斯金字塔最底层,将其进行高斯低通滤波,之后对其进行隔行隔列的下采样,得到的图像与源图像在较低分辨率上近似,分辨率是源图的一半(高斯金字塔的第一层G1)。重复上述操作,得到下一层高斯金字塔。
(十三)图像的拉普拉斯梯度锐化
环境:Windows10专业版 + IDEA2021.2.3 + jdk11.0.1 + OpenCV-460.jar 系列文章: (一)Python+GDAL实现BSQ,BIP,BIL格式的相互转换 (二)BSQ,BIL,BIP存储格式的相互转换算法 (三)单波段图像的伪彩色合成:密度分割(含介绍OpenCV中的Mat类) (四)图像的%2线性拉伸 (五)图像的标准假彩色合成 (六)图
信号系统之拉普拉斯变换
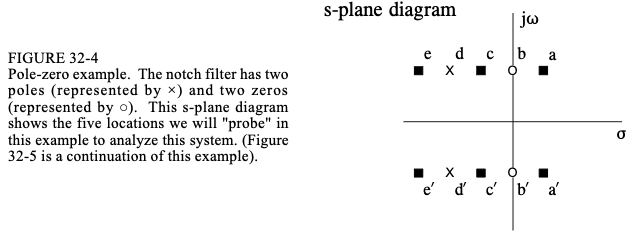
拉普拉斯变换是一种在信号连续时分析的技术。 z 变换是离散情况下使用的技术。 1 s-Domain的本质 拉普拉斯变换是一种成熟的用于求解微分方程的数学技术。与所有变换一样,拉普拉斯变换根据一组固定的规则或方程将一个信号变为另一个信号。 如图32-1所示,拉普拉斯变换将时域信号变为s域信号,也称为s-plane。时域信号是连续的,延伸到正无穷大和负无穷大,并且可以是周期性的或非周期性的。拉普
用拉普拉斯算子进行滤波
from; http://hi.baidu.com/archiless/blog/item/97a97cd9a12e25e939012fc7.html %function PicOut=Lap_edge(PicInput,thresh) PicInput=imread('c:/boat.png'); thresh=45; % 本程序能够将BMP格式的黑白灰度
OpenCV学习笔记-拉普拉斯变换
拉普拉斯变换的函数为: Laplace 计算图像的 Laplacian 变换 void cvLaplace( const CvArr* src, CvArr* dst, int aperture_size=3 ); src 输入图像. dst 输出图像. aperture_size 核大小 (与 cvSobel 中定义一样). 函数 cvLaplace 计算输入图像
高斯拉普拉斯锐化(边缘检测)vc实现
高斯拉普拉斯锐化(边缘检测)vc实现 -LoG锐化,边缘检测。 void CSDIELSView::OnSharpeningGaussianAndLaplace(){//程序编制:李立宗 lilizong@gmail.com//2012-8-12if(myImage1.IsNull())OnOpenResourceFile();if(!myImage2.IsNull())my
图像锐化拉普拉斯vc代码
void CSDIELSView::OnSharpeningLaplace(){//程序编制:李立宗 lilizong@gmail.com//2012-8-11if(myImage1.IsNull())OnOpenResourceFile();if(!myImage2.IsNull())myImage2.Destroy();if(myImage2.IsNull()){myImag
流形学习之拉普拉斯特征映射
首先,我们说一下流形学习;接着,我们重点介绍拉普拉斯特征映射算法;最后,本文将给出拉普拉斯特征特征映射算法代码。 流形学习 流形学习是一种非线性降维方法,能够从高维数据中发现低维流形结构,得到高维和低维之间的映射关系,从而实现数据的维数约简。**为什么要实现特征约简?**因为高维的数据存在数据量大并且高维数据输入到网络模型中训练难度较大,耗费时间长。 流形学习展示图,其中包括Isomap(等距