graph Laplacian 拉普拉斯矩阵

本文主要是介绍graph Laplacian 拉普拉斯矩阵，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

拉普拉斯矩阵是个非常巧妙的东西，它是描述图的一种矩阵，在降维，分类，聚类等机器学习的领域有很广泛的应用。

什么是拉普拉斯矩阵

拉普拉斯矩阵

　　先说一下什么是拉普拉斯矩阵，英文名为Laplacian matrix，其具体形式得先从图说起，假设有个无向图如下所示， 
　　

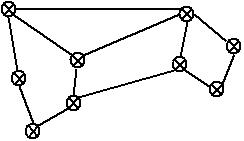
　　其各个点之间的都有相应的边连接，我们用某个指标（这地方可以任意选择，比如欧氏距离、测地距离、或者高斯相似度等）来衡量两个点的相似度，表示为 W=∑wij ，没有边连接的其相似度自然为零， W 是个对称矩阵；某个点的与所有点的相似度之和，表示为 D=dig(d);d=rowSum(W) ； D 是个对角阵；我们的拉普拉斯矩阵则是 L=D−W

拉普拉斯矩阵的性质

　　性质： 
　　（1） L 是半正定矩阵。 
　　（2） L 的最小特值为0，对应特向为全1列向量。 
　　（3）对 Lf=λDf 有 m 个非负实特征值， 0=λ1≤λ2≤...≤λm . 
　　（4）对于任意一个属于实向量 f∈Rm ，都有此公式成立： 
　　 fTLf=12∑mi,j=1wij(fi−fj)2  
　　它又有什么用处呢？跟目标是有关系的，哈哈~ 
　　证明如下：　　 f 为 m∗1 的实数列向量 
　　 fTLf=fTDf−fTWf  
　　 =fT∗dig(d)∗f−fTWf  
　　 =∑mi=1dif2i−∑mj=1[∑i=1fj∗wij]fj  
　　因为 ∑mi,j=1fifjwij=∑mj=1[∑mi=1fiwij]yj 所以 
　　 =∑mi=1dif2i−∑mi,j=1fifjwij 　　 
　　 =12[∑mi=1dif2i−2∑mi,j=1fifjwij+∑mj=1djf2j]  
　　 =12∑mi,j=1wij(fi−fj)2  
　　

拉普拉斯特征映射

　　拉普拉斯特征映射将处于流形上的数据，在尽量保留原数据间相似度的情况下，映射到低维下表示。 
　　其步骤如下： 
　　1. 构造近邻图（用近邻图图近似流形） 
　　　　1.1 近邻条件 ||xi−xj||2≤ϵ ，  xi 表示第 i 个样本。 
　　　　1.2 K近邻 
　　2. 计算边权重（即样本间相似度） 
　　　　2.1 热核  wij=⎧⎩⎨exp(−||xi−xj||2t)0节点i与j相连不相连  
　　　　2.2 简单形式 wij={10xi与xj相连不相连  
　　3. 特征映射 
　　　　求解 Lf=λDf ；广义特征值问题。 
　　　　得到解如下：（特向和特值） 
　　　　 {Lf0=λ0Df0;Lf1=λ1Df1;...Lfm=λmDfm0=λ0≤λ1≤...≤λm  
　　　　取小的前 k 个 f 来嵌入到 k 维欧氏空间里。 
　　　　 xi−>(f1(xi),f2(xi),...,fk(xi))  
　　至于为神马 min[∑mi,j=1wij∗||yi−yj||2等价于tr(YTLY)] ，愣是没有看出所以然来，哎~ 
　　倒腾了一大通，终于把为什么目标 min[∑mi,j=1wij||Si−Sj||2] 等价于 min[yTLy] 给搞明白了。 y∈Rm  
　　具体解释如下图所示：（左侧是基本思路，中间是核心推导，右侧是直观理解） 
　　

　　但是 还有个问题没有解决 ，就是为什么 min(yTLy) 等价于 min[tr(yTLy)] ，并且转换成立找最小的广义特征值 Ly=λDy ？ 
　　 只能从直觉上理解 ， yTLy 可以化为 λ1z21+λ2z22+...+λmz2m 的样子，最小化这个平方和的式子，也就是最小化其系数和，也就是最小化特值，也就是找对应特向。拉普拉斯矩阵是实对称矩阵，不同特值对应正交特向，可以通过正交变换（此处用到了特向）得到形如平方和的标准二次型。 
　　为什么是用广义特征值 Ly=λDy 没有搞懂，囧？ 
　　 拉普拉斯映射就是直接在低维下找到样本，使得所有样本保持原来的相似度。

应用于降维

　　求解广义特征向量，取前几个非零最小特值对应的特向，即为原数据在低维下的表示。

应用于聚类

　　三个概念： 
　　（1）对于邻接矩阵，定义图中A子图与B子图之间的所有边的权重之和为： W(A,B)=∑i∈A,j∈BWij  
　　 W 为所有边的权重，及样本间相似度矩阵。 
　　（2）与某点的所有边的权重和定义为该顶点的度 di=∑mj=1Wij  
　　（3）Graph Cut，就是把一个图的一些边切断，把一个图变为若干独立的子图，而这些被切断的边的权重之和称为Cut值。 
　　对于如下图，我们想找到某个割把整个图分成两个子图。 
　　

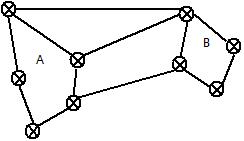
　　 Cut(A,B)=∑i∈A,j∈Bwij  
　　上面的割会把孤立节点分割出来，为避免这种情况，出现了RatioCut以及NormalizedCut： 
　　 RatioCut=cut(A,B)|A|+cut(A,B)|B|  
　　 NCut=cut(A,B)vol(A)+cut(A,B)vol(B)  
　　其中 |A| 表示 A 中节点的数目， vol(A)=∑i∈Awij ，此两者都可以算作 A 的大小的一种度量 。 
　　 谱聚类，由最小割入手，转换到最小化二次型求解，其中包含了拉普拉斯映射降维的思想。  
　　例如，取 qi={c1c2i∈Ai∈B  
　　则 Cut(A,B)=∑i∈A,j∈Bwij  
　　 ∝∑mi=1∑mj=1wij(qi−qj)2=qTLq 这里跟上面的一样了。这里做了 松弛处理 ， 即q不再是取值为某两个值了，而是任意实数 。 
　　Rayleigh quotient(瑞利商) R(L,q)=qTLqqTq  
　　其最大值和最小值分别等于矩阵 L 最大和最小的特值分别对应的特向。 
　　因此，最小化割问题，也就变成了找 L 的非零最小特值对应特向的问题了。求解特向： Lq=λq ，排序特值，选择特向，传统聚类方法开搞。 
　　我们想把原图分成两个子图，肯定找到一个最小割对应的特向即可，那么要是想分成3个子图，那就需要最小割和次小割所对应的特向解即可。（这个地方这样理解会直观一些， 最小割对应的特向是降维后包含分割为两个子图的信息，而最小割加次小割对应的特向则是包含分割为3个子图的信息） 聚几类，则取前几个最小非零特值对应的特向的意义就在于此。 
　　 谱图理论需要找个时间看看。

小结

　　1）拉普拉斯矩阵是一种图的矩阵表示。 
　　2）拉普拉斯映射是在保持原流形数据相似度的情况下，直接降维到低维空间。 
　　3）谱聚类是通过最小割，刚好借助了拉普拉斯映射的思想，从而用携带切割信息的特向来表征原流形数据，再去聚类。（相比于传统聚类，谱聚类更侧重于数据相似度信息的保留，更具有针对性，计算效率也更高） 
　　三者紧密联系，又不能混为一谈。 
几个参考： 
1）化二次型为标准型 
http://student.zjzk.cn/course_ware/web-gcsx/gcsx/chapter5/chapter5_2_1.htm 
2）一个关于拉普拉斯矩阵的博客 
http://blog.sciencenet.cn/blog-261330-751483.html 
3）一个谱聚类的博客 
http://blog.pluskid.org/?p=287 
4）广义特征值的介绍 
http://webcache.googleusercontent.com/search?q=cache:_85fSHsIv3MJ:https://zh.wikipedia.org/zh-cn/%25E7%2589%25B9%25E5%25BE%2581%25E5%2590%2591%25E9%2587%258F+&cd=1&hl=zh-CN&ct=clnk&gl=cn&lr=lang_en%7Clang_zh-CN%7Clang_zh-

转自：http://blog.csdn.net/yujianmin1990/article/details/48420483

这篇关于graph Laplacian 拉普拉斯矩阵的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---