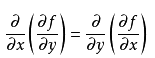矩阵专题
hdu 4565 推倒公式+矩阵快速幂
题意 求下式的值： Sn=⌈ (a+b√)n⌉%m S_n = \lceil\ (a + \sqrt{b}) ^ n \rceil\% m 其中： 0<a,m<215 0< a, m < 2^{15} 0<b,n<231 0 < b, n < 2^{31} (a−1)2<b<a2 (a-1)^2< b < a^2 解析 令： An=(a+b√)n A_n = (a +
hdu 6198 dfs枚举找规律+矩阵乘法
number number number Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Problem Description We define a sequence F : ⋅ F0=0,F1=1 ; ⋅ Fn=Fn
线性代数|机器学习-P35距离矩阵和普鲁克问题
文章目录 1. 距离矩阵2. 正交普鲁克问题3. 实例说明 1. 距离矩阵 假设有三个点 x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3,三个点距离如下： ∣ ∣ x 1 − x 2 ∣ ∣ 2 = 1 , ∣ ∣ x 2 − x 3 ∣ ∣ 2 = 1 , ∣ ∣ x 1 − x 3 ∣ ∣ 2 = 6 \begin{equation} ||x
【线性代数】正定矩阵，二次型函数
本文主要介绍正定矩阵，二次型函数，及其相关的解析证明过程和各个过程的可视化几何解释（深蓝色字体）。 非常喜欢清华大学张颢老师说过的一段话：如果你不能用可视化的方式看到事情的结果，那么你就很难对这个事情有认知，认知就是直觉，解析的东西可以让你理解，但未必能让你形成直觉，因为他太反直觉了。 正定矩阵 定义 给定一个大小为 n×n 的实对称矩阵 A ，若对于任意长度为 n 的非零向量 ，有 恒成
python科学计算：NumPy 线性代数与矩阵操作
1 NumPy 中的矩阵与数组 在 NumPy 中，矩阵实际上是一种特殊的二维数组，因此几乎所有数组的操作都可以应用到矩阵上。不过，矩阵运算与一般的数组运算存在一定的区别，尤其是在点积、乘法等操作中。 1.1 创建矩阵 矩阵可以通过 NumPy 的 array() 函数创建。矩阵的形状可以通过 shape 属性来访问。 import numpy as np# 创建一个 2x3 矩阵mat
【UVA】10003-Cutting Sticks（动态规划、矩阵链乘）
一道动态规划题，不过似乎可以用回溯水过去，回溯的话效率很烂的。 13988658 10003 Cutting Sticks Accepted C++ 1.882 2014-08-04 09:26:49 AC代码： #include<cstdio>#include<cstring>#include<iostream>#include<algorithm>#include
算法练习题17——leetcode54螺旋矩阵
题目描述 给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。 代码 import java.util.*;class Solution {public List<Integer> spiralOrder(int[][] matrix) {// 用于存储螺旋顺序遍历的结果List<Integer> result = new ArrayList
线性代数 第六讲 特征值和特征向量_相似对角化_实对称矩阵_重点题型总结详细解析
文章目录 1.特征值和特征向量1.1 特征值和特征向量的定义1.2 特征值和特征向量的求法1.3 特征值特征向量的主要结论 2.相似2.1 相似的定义2.2 相似的性质2.3 相似的结论 3.相似对角化4.实对称矩阵4.1 实对称矩阵的基本性质4.2 施密特正交化 5.重难点题型总结5.1 判断矩阵能否相似对角化5.2 已知两个矩阵相似，求某个矩阵中的未知参数5.3 相似时，求可逆矩阵P，使
最大子矩阵和问题归纳总结
一，最大子矩阵问题： 给定一个n*n(0< n <=100)的矩阵，请找到此矩阵的一个子矩阵，并且此子矩阵的各个元素的和最大，输出这个最大的值。 Example： 0 -2 -7 0 9 2 -6 2 -4 1 -4 1 -1 8 0 -2 其中左上角的子矩阵： 9 2 -4 1 -1 8 此子矩阵的值为9+2+(-4)+1+(-1)+8=15。 二，分析 子矩阵是在矩阵
3.门锁_STM32_矩阵按键设备实现
概述 需求来源： 门锁肯定是要输入密码，这个门锁提供了两个输入密码的方式：一个是蓝牙输入，一个是按键输入。对于按键输入，采用矩阵按键来实现。矩阵按键是为了模拟触摸屏的按键输入，后续如果项目结束前还有时间就更新为触摸屏按键输入。 矩阵按键开发整体思路： 由于矩阵按键就是GPIO的控制，所以不进行芯片和设备的分层编写，控制写在同一个文件中，最终向应用层提供一个接口。 代码层级关系：
1051 找矩阵中的鞍点
### 思路 1. 输入一个3行4列的整数矩阵。 2. 遍历每一行，找到每一行的最大值及其列索引。 3. 检查该列索引对应的列中是否是最小值。 4. 如果是，则输出该值；如果没有找到鞍点，输出“NO”。 ### 伪代码 1. 初始化一个3行4列的矩阵 `matrix`。 2. 输入矩阵的元素。 3. 遍历每一行： - 找到每一行的最大值及其列索引。 - 检查该列索引对应的列中是否
MATLAB中的矩阵在目标规划中的应用_以linprog为例
目标规划是一种数学规划方法，它允许在多个目标之间进行权衡，以找到最优解。 在MATLAB中，可以使用优化工具箱中的函数来求解目标规划问题。例如，`linprog` 函数可以用于求解线性规划问题，而 `fmincon` 函数可以用于求解有约束的非线性规划问题。对于多目标规划，可以使用 `fgoalattain` 函数来求解，该函数允许设置目标函数希望达到的目标值和权重。 在数学方程模型建立完成之
【R语言数据类型】深入了解 向量、矩阵、数据框、列表
R语言数据类型有向量、矩阵、数据框、列表。下面我们来深入了解下： vector 的划分 R中的vector分为两类，atomic和list，二者的区别在于,前者元素类型必须相同，后者可以不同。前者的代表是向量和矩阵，后者的代表是list和数据框。 创建向量、矩阵、数据框、列表 # atomica <- 1:5b <- letters[1:5]c <- 1:10mat <- matr
【MATLAB】矩阵的合并
矩阵的合并是指将两个或者多个矩阵合并到一起构成一个新的矩阵。矩阵标识符方括号 [ ]，不仅可以用来创建新的矩阵，还可以用来将若干个矩阵合并到一起。表达式 C = [A B] 将矩阵A和B在水平方向上合并到一起，而表达式C=[A;B]则将矩阵A和B在竖直方向上合并到一起。 例子： 求矩阵A和B在竖直方向上合并到一起后得到的矩阵C。 clc;clear;closerand('state',0);
JD 1474：矩阵幂
OJ题目：click here~~ 题目分析：经典题目，矩阵快速幂。 typedef vector<int> vec ;typedef vector<vec> mat ;int n ;mat mul(mat &A , mat &B){mat C(n , vec(n)) ;for(int i = 0;i < n;i++)for(int j = 0;j < n;j++)for(int k
JD 1497：面积最大的全1子矩阵
OJ题目：click here~~ 题目分析：经典题目。。 const int maxn = 1008 ;int n , m ;int x[maxn][maxn] ;int h[maxn] , Left[maxn] , Right[maxn] ;void check(int &a , int b){if(b > a) a = b ;}void all_1_matrix()
《机器学习》 基于SVD的矩阵分解 推导、案例实现
目录 一、SVD奇异值分解 1、什么是SVD 2、SVD的应用 1）数据降维 2）推荐算法 3）自然语言处理 3、核心 1）什么是酉矩阵 2）什么是对角矩阵 4、分解过程 二、推导 1、如何求解这三个矩阵 1）已知： 2）根据酉矩阵的特点即可得出：
Hessian矩阵判定极值之MATLAB实现符号解
By WC 1.9 .2015 1.Hessian矩阵 其定义如下： 如果函数f在D区域内二阶连续可导，那么黑塞矩阵H(f) 在 D 内为对称矩阵。原因是：如果函数f连续，则二阶偏导数的求
python 实现matrix exponentiation矩阵求幂算法
matrix exponentiation矩阵求幂算法介绍 矩阵求幂算法（Matrix Exponentiation）是一种通过利用矩阵乘法的结合律来高效地计算矩阵的幂的算法。这种方法特别适用于在算法竞赛和计算机科学领域中解决需要快速计算矩阵幂的问题，如求解线性递推关系、图论中的路径计数等。 基本思想 矩阵求幂算法的基本思想类似于整数快速幂算法（快速幂算法），通过递归或迭代的方式将矩阵幂的计
【AI】张量的秩（阶）与矩阵的秩和阶的区别
在阅读MindSpore文档时，笔者对这段话不太理解，遂求助ChatGPT. 矩阵的秩是矩阵中线性无关的行或者列，矩阵的阶就是矩阵中的行数和列数。 而张量的秩和阶是一个概念，指的是张量的维度（是1维的，二维的还是高维的）
java常用算法之螺旋矩阵
给定一个m*n矩阵，返回所有元素在矩阵中的螺旋序列，例如： [ [ 1, 2, 3 ], [ 4, 5, 6 ], [ 7, 8, 9 ] ] 返回[1,2,3,6,9,8,7,4,5]. 算法实现如下： public static List<Integer> spiralMatrix(int source[][]) {List<Integer> result = new Ar
庞峰Opencv学习(二)--对矩阵结构体CvMat的基本操作
1. CvMat结构体：(注释) typedef struct CvMat{int type; //数据类型以 CV_N{U|S|F}C{1,2,3...}表示int step; //表示一行有多少个字，在32位操作系统中，一个字为4个字节/* for internal use only */int* refcount;int hdr_refcount;union //
6、LVGL控件-线条、图片、按钮矩阵
本篇文章目录导航 ♠♠ LVGL控件-线条、图片、按钮矩阵 ♣♣♣♣ 一、LVGL 线条部件 ♦♦♦♦♦♦♦♦ 1.1 线条部件组成部分 ♦♦♦♦♦♦♦♦ 1.2 线条部件基本API ♦♦♦♦♦♦♦♦ 1.3 实验小演示 ♣♣♣♣ 二、LVGL 图片部件 ♦♦♦♦♦♦♦♦ 2.1 图片部件组成部分 ♦♦♦♦♦♦♦♦ 2.2 图片部件基本API ♦♦♦♦♦♦♦♦ 2.3 实验小演示（基础操作） ♦
【ACDream】 1093 女神的正多面体 矩阵快速幂
题目大意：给你三种正多边形，给你起点s，终点e以及最多行走的步数k，问有多少种路径方案（路径中只要有一个顶点不同即视为不同）。 题目分析： 可以通过矩阵快速幂求解。 为每个正多边形（最多三个）构建一个邻接矩阵A，然后第K步的方案数即为A^k。 结果即为A^1 + A^2 + A^3 + ...... + A^k. 对于这种形式的矩阵运算，我们可以把它拆分成： k为奇：ans = （
齐次变换矩阵的原理与应用
齐次变换矩阵的原理与应用 通过齐次变换矩阵，可以描述机械臂末端执行器（法兰）在三维空间中的平移和旋转操作。该矩阵结合了旋转和平移信息，用于坐标变换。 1. 齐次变换矩阵的基本形式 一个齐次变换矩阵 T是一个 4x4 矩阵，表示刚体的旋转和平移： T = [ R t 0 1 ] = [ r 11 r 12 r 13 x r 21 r 22 r 23 y r 31 r 32 r 33 z 0