数学之路-python计算实战(21)-机器视觉-拉普拉斯线性滤波

本文主要是介绍数学之路-python计算实战(21)-机器视觉-拉普拉斯线性滤波，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

拉普拉斯线性滤波,.边缘检测

  Laplacian

Calculates the Laplacian of an image.

C++:  void  Laplacian (InputArray  src, OutputArray  dst, int  ddepth, int  ksize=1, double  scale=1, double  delta=0, int  borderType=BORDER_DEFAULT  )

Python:   cv2. Laplacian (src, ddepth [, dst [, ksize [, scale [, delta [, borderType ] ] ] ] ] ) → dst

C:  void  cvLaplace (const CvArr*  src, CvArr*  dst, int  aperture_size=3  )

Python:   cv. Laplace (src, dst, apertureSize=3 ) → None

Parameters:

src – Source image. dst – Destination image of the same size and the same number of channels as src . ddepth – Desired depth of the destination image. ksize – Aperture size used to compute the second-derivative filters. See getDerivKernels() for details. The size must be positive and odd. scale – Optional scale factor for the computed Laplacian values. By default, no scaling is applied. See getDerivKernels() for details. delta – Optional delta value that is added to the results prior to storing them in dst . borderType – Pixel extrapolation method. SeeborderInterpolate() for details.

The function calculates the Laplacian of the source image by adding up the second x and y derivatives calculated using the Sobel operator:

This is done when ksize > 1 . When ksize == 1 , the Laplacian is computed by filtering the image with the following  aperture:

Laplace

计算图像的 Laplacian 变换

void cvLaplace( const CvArr* src, CvArr* dst, int aperture_size=3 );

src

输入图像.

dst

输出图像.

aperture_size

核大小 (与 cvSobel 中定义一样).

函数 cvLaplace 计算输入图像的 Laplacian变换，方法是先用 sobel 算子计算二阶 x- 和 y- 差分，再求和:

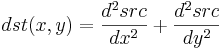
对 aperture_size=1 则给出最快计算结果，相当于对图像采用如下内核做卷积：

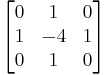
本博客所有内容是原创，如果转载请注明来源

http://blog.csdn.net/myhaspl/

# -*- coding: utf-8 -*-   
#线性锐化滤波，拉普拉斯图像变换
#code:myhaspl@myhaspl.com
import cv2fn="test6.jpg"
myimg=cv2.imread(fn)
img=cv2.cvtColor(myimg,cv2.COLOR_BGR2GRAY)jgimg=cv2.Laplacian(img,-1)
cv2.imshow('src',img)
cv2.imshow('dst',jgimg)
cv2.waitKey()
cv2.destroyAllWindows()

这篇关于数学之路-python计算实战(21)-机器视觉-拉普拉斯线性滤波的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---