线性专题

线性因子模型 - 独立分量分析（ICA）篇

序言线性因子模型是数据分析与机器学习中的一类重要模型，它们通过引入潜变量（ latent variables \text{latent variables} latent variables）来更好地表征数据。其中，独立分量分析（ ICA \text{ICA} ICA）作为线性因子模型的一种，以其独特的视角和广泛的应用领域而备受关注。 ICA \text{ICA} ICA旨在将观察到的复杂信号

✨机器学习笔记（二）—— 线性回归、代价函数、梯度下降

1️⃣线性回归（linear regression） f w , b ( x ) = w x + b f_{w,b}(x) = wx + b fw,b(x)=wx+b 🎈A linear regression model predicting house prices：如图是机器学习通过监督学习运用线性回归模型来预测房价的例子，当房屋大小为1250 f e e t 2 feet^

【高等代数笔记】线性空间（一到四）

3. 线性空间令 K n : = { ( a 1 , a 2 , . . . , a n ) ∣ a i ∈ K , i = 1 , 2 , . . . , n } \textbf{K}^{n}:=\{(a_{1},a_{2},...,a_{n})|a_{i}\in\textbf{K},i=1,2,...,n\} Kn:={(a1,a2,...,an)∣ai∈K,i=1,2,...,n

带头结点的线性链表的基本操作

持续了好久，终于有了这篇博客，链表的操作需要借助图像模型进行反复学习，这里尽可能的整理并记录下自己的思考，以备后面复习，和大家分享。需要说明的是，我们从实际应用角度出发重新定义了线性表。一. 定义从上一篇文章可以看到，由于链表在空间的合理利用上和插入、删除时不需要移动等优点，因此在很多场合下，它是线性表的首选存储结构。然而，它也存在某些实现的缺点，如求线性表的长度时不如顺序存储结构的

浙大数据结构：02-线性结构4 Pop Sequence

这道题我们采用数组来模拟堆栈和队列。简单说一下大致思路，我们用栈来存1234.....，队列来存输入的一组数据，栈与队列进行匹配，相同就pop 机翻 1、条件准备 stk是栈，que是队列。 tt指向的是栈中下标，front指向队头，rear指向队尾。初始化栈顶为0，队头为0，队尾为-1 #include<iostream>using namespace std;#defi

深度学习与大模型第3课：线性回归模型的构建与训练

文章目录使用Python实现线性回归：从基础到scikit-learn1. 环境准备2. 数据准备和可视化3. 使用numpy实现线性回归4. 使用模型进行预测5. 可视化预测结果6. 使用scikit-learn实现线性回归7. 梯度下降法8. 随机梯度下降和小批量梯度下降9. 比较不同的梯度下降方法总结使用Python实现线性回归：从基础到scikit-learn 线性

C#中的各种画刷， PathGradientBrush、线性渐变（LinearGradientBrush）和径向渐变的区别

在C#中，画刷（Brush）是用来填充图形（如形状或文本）内部区域的对象。在.NET框架中，画刷是System.Drawing命名空间的一部分，通常用于GDI+绘图操作。以下是一些常用的画刷类型： SolidBrush：用于创建单色填充的画刷。HatchBrush：用于创建具有图案填充的画刷。TextureBrush：用于创建具有图像纹理填充的画刷。LinearGradientBrush：用于创

(感知机-Perceptron)—有监督学习方法、非概率模型、判别模型、线性模型、参数化模型、批量学习、核方法

定义假设输入空间（特征空间）是 χ \chi χ ⊆ R n \subseteq R^n ⊆Rn,输出空间是y = { + 1 , − 1 } =\{+1,-1 \} ={+1,−1} 。输入 x ∈ χ x \in \chi x∈χ表示实例的特征向量，对应于输入空间（特征空间）的点；输出 y ∈ y \in y∈y表示实例的类别。由输入空间到输出空间的如下函数： f ( x ) = s

逻辑回归与线性回归的目标函数和应用场景比较

概述逻辑回归和线性回归是两种常用的预测模型，它们在目标函数和应用场景上存在显著差异。本文将详细比较这两种回归模型，并提供相应的代码示例。线性回归线性回归是一种预测连续数值的模型，其目标是找到特征( X )和目标变量( Y )之间的线性关系。线性回归的目标函数是最小化预测值和实际值之间的平方差，即均方误差（MSE）。目标函数线性回归的损失函数是均方误差： [ J(\theta)

【深度学习】线性回归的从零开始实现与简洁实现

前言我原本后面打算用李沐老师那本《动手学深度学习》继续“抄书”，他们团队也免费提供了电子版(https://zh-v2.d2l.ai/d2l-zh-pytorch.pdf)。但书里涉及到代码，一方面展示起来不太方便，另一方面我自己也有很多地方看不太懂。这让我开始思考起我“抄书”的意义了。如果都是文字，我感觉抄起来可以加深印象，在抄的同时理解并思考。但是如果涉及到代码，我没办法在抄的时候

[机器学习]线性回归算法

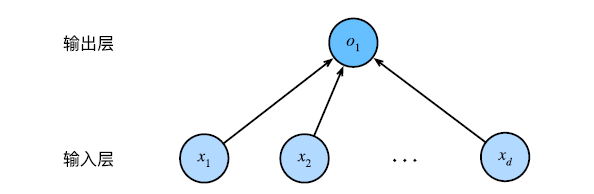
1 线性回归简介概念：利用回归方程（函数）对一个或多个自变量（特征值）和因变量（目标值）之间关系进行建模的一种分析方式。 weight：权重；bias 偏置线性回归分类：一元线性回归、多元线性回归应用场景：只要目标值连续，就使用线性回归 2 线性回归问题求解 2.1 线性回归API from sklearn.linear_model import LinearRegre

机器学习算法：监督学习中的线性回归

在机器学习领域，线性回归是一种经典的监督学习算法，用于预测连续数值型的目标变量。它假设输入特征和输出结果之间存在线性关系。线性回归模型的目标是找到一条直线（在二维空间中）或一个平面（在三维空间中），使得这条直线或平面尽可能地接近所有的训练数据点。线性回归的数学表达线性回归模型可以表示为： [ y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \ldots

数据分析：R语言计算XGBoost线性回归模型的SHAP值

禁止商业或二改转载，仅供自学使用，侵权必究，如需截取部分内容请后台联系作者! 文章目录介绍SHAP用途计算方法：应用加载R包导入数据数据预处理函数模型介绍 SHAP（SHapley Additive exPlanations）值是一种解释机器学习模型预测的方法。它基于博弈论中的Shapley值概念，用于解释任何机器学习模型的输出。 SHAP用途解释性：机器学习模型

内存管理篇-21 虚拟内存管理：线性映射区

1.线性映射区的定义这部分讲线性映射区的内容。一般老的嵌入式平台，它内存很小只有几百兆，都会直接把整个物理内存映射到线性映射区了，只有当物理内存大于1GB以上，线性映射区无法cover的时候就把剩下的放到高端内存。所以这个区域是最简单的。线性映射区一般是指内核空间的某个部分，直接映射到低端内存的区域。并且他们之间是线性映射的。 PAGE_O

【深度学习详解】Task2 分段线性模型-引入深度学习 Datawhale X 李宏毅苹果书 AI夏令营

前言《苹果书》第一章的内容包括机器学习基础 -> 线性模型 -> 分段线性模型 -> 引入深度学习这一篇章我们继续后续内容 ~ 其中涉及到“激活函数”的作用理解：除了开源项目 - 跟李宏毅学深度学习(入门) 之外，还有 @3Blue1Brown 的神经网络和 @StatQuest 的深度学习视频内容辅助。 🍎 🍎 系列文章导航【深度学习详解】Task1 机器学习基础-

数论 - n元线性同余方程的解法

note:n元线性同余方程因其编程的特殊性，一般在acm中用的很少，这里只是出于兴趣学了一下 n元线性同余方程的概念: 形如：(a1*x1+a2*x2+....+an*xn)%m=b%m ..................(1) 当然也有很多变形，例如：a1*x1+a2*x2+...+an*xn+m*x(n+1)=b.这两个都是等价的。判断是否有解:

简述CCS平面线性光源

光源在机器视觉系统中起着重要作用，不同环境、场景及应用合适光源都不一样，今天我们来看看LFX3-PT系列平面线性光源。它是最适合检测镜面物体的凹凸,外壳小巧的光源。备有根据检测条件可选的2种线间距。1mm型（型号末尾：A）、2mm型（型号末尾：B）。特点： 1、将导光板表面的印刷图案从点状更改为线状，可对同轴光源难以检测出的镜面物体上，“不明显的凹凸”进行提取并实现成像。

《数字信号处理》学习04-离散时间系统中的线性时不变系统

目录一，系统及离散时间系统二，离散时间系统中的线性时不变系统 1，线性系统 1) 可加性 2) 比例性(齐次性) 3）叠加原理(叠加性质) 2，时不变系统(移不变系统) 通过前几篇文章的学习，此时我对序列的相关概念和运算已经有所掌握，接下来我将开始学习新的概念“离散时间系统中的线性时不变系统”，一，系统及离散时间系统首先需要知道系统的概念，在《信

Datawhale X 李宏毅苹果书 AI夏令营 - 跟李宏毅学深度学习（入门之线性模型）

文章目录一、线性模型是什么？二、线性模型的特点三、简单举例理解3.1、预测未来某一天点击量3.2、分段线性曲线总结一、线性模型是什么？在深度学习中，线性模型是一种简单但基础且广泛应用的数学模型。它的基本形式是一个线性方程，如y = wx + b，其中y是预测输出，x是输入特征，w是权重参数，b是偏置项（也称为截距）。线性模型假设输入与输出之间存在线性关系，即输出是输

8种进行简单线性回归的方法分析与讨论

以下是八种进行简单线性回归的方法及其分析与讨论：二乘法（OLS）：分析：通过化预测值与实际值之间的平方误差来估计回归系数。讨论：简单直观，适用于大多数线性回归问题。但对于数据中存在异常值或噪声时，可能不够鲁棒。梯度下降法：分析：通过迭代优化算法调整回归系数，以化损失函数。讨论：适用于大规模数据集和复杂模型，但需要选择合适的学习率，并可能需要较长的训练时间。正规方程法：

数学建模强化宝典（10）多元线性回归模型

一、介绍多元线性回归模型（Multiple Linear Regression Model）是一种用于分析多个自变量（解释变量、预测变量）与单个因变量（响应变量、被预测变量）之间线性关系的统计模型。这种模型假设因变量的变化可以通过自变量的线性组合来近似地表示，同时考虑了一个误差项来捕捉模型未能解释的变异性。二、模型形式多元线性回归模型的一般形式可以表示为： Y=β

TensorFlow介绍二-线性回归案例

一.案例步骤 1.准备数据集：y=0.8x+0.7 100个样本 2.建立线性模型，初始化w和b变量 3.确定损失函数（预测值与真实值之间的误差），均方误差 4.梯度下降优化损失二.完整功能代码： import osos.environ['TF_CPP_MIN_LOG_LEVEL']='2'import tensorflow as tfdef linear_regressi

002线性逻辑结构——线性表

目录 1.数据之间的逻辑关系 2.存储结构的实现 2.1顺序存储结构实现线性表：对该顺序表进行一系列的增删改查： ①增： Ⅰ）顺序添加： Ⅱ）插入添加： ②删： ③改： ④查：输出整体代码示例 1.数据之间的逻辑关系线性表：具有相同数据类型的有限个（n）数据元素的序列

《西瓜书》第三章线性模型手写版笔记

《西瓜书》第三章线性模型手写版笔记文章目录《西瓜书》第三章线性模型手写版笔记3.0 知识点总览3.1 线性回归(Linear Regression)求解的推导过程3.1.1 单变量线性回归3.1.2 多变量线性回归3.1.3 对数线性回归 3.2 逻辑回归(Logistic Regression)3.3 线性判别(LDA)3.4 多分类学习的拆分策略3.5 处理类别不平衡问题三

线性结构队列栈知识点（软件设计师）

线性结构 1.线性表2.线性表存储结构顺序存储链式存储 3.栈4.队列5.串 1.线性表线性表是最简单、最基本的数据结构。线性表常采用顺序存储和链式存储，主要的基本操作是插入、删除和查找等 2.线性表存储结构顺序存储插入、删除移动元素查找时间复杂度O(1) 可以随机存取表中元素链式存储末尾插入时间复杂度O(1)，删除O(n)查找时间复杂度O(n

5.4分段线性灰度变换

目录实验原理分段线性灰度变换的概念变换函数的形式示例代码1 示例结果1 示例代码2 示例结果2 示例代码3 运行结果3 示例代码4 运行结果4 实验原理在OpenCV中，分段线性灰度变换（Piecewise Linear Gray Level Transformation）是一种更复杂的图像处理技术，它允许对图像的不同灰度区间应用不同的线性变换。这种方法