本文主要是介绍简述CCS平面线性光源,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
光源在机器视觉系统中起着重要作用,不同环境、场景及应用合适光源都不一样,今天我们来看看LFX3-PT系列平面线性光源。它是最适合检测镜面物体的凹凸,外壳小巧的光源。备有根据检测条件可选的2种线间距。1mm型(型号末尾:A)、2mm型(型号末尾:B)。
特点:
1、将导光板表面的印刷图案从点状更改为线状,可对同轴光源难以检测出的镜面物体上,“不明显的凹凸”进行提取并实现成像。
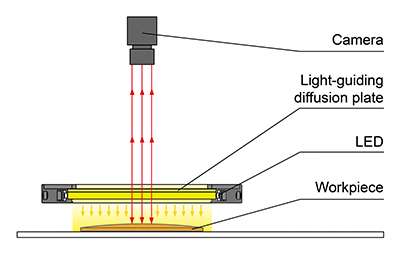
LFX3-100-PT
2、提供2种线间距
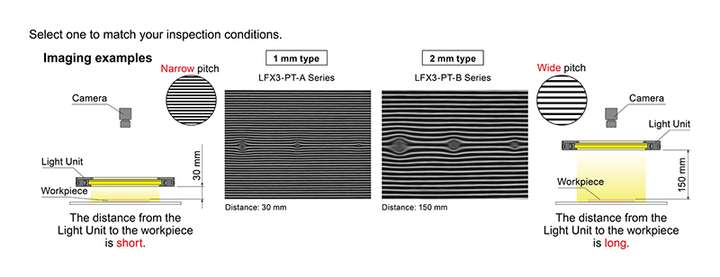
可根据检测条件进行选择
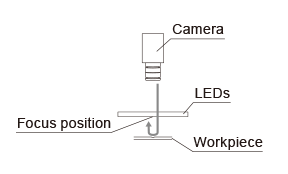
3、为了获得适合的图像
安装光源时,使现状图案能够投影到被测物体上,通常情况下,请将相机焦距对准光源的现状图案,而非被测物体。成像中如有干涉条纹,可以尝试放大相机光圈;光源与被测物体之间拉开距离。
成像条件(相机与被测物体之间的距离,焦距位置,光圈大小),和光源位置因不同检测而异。
成像实例:
金属板外观成像

金属板外观成像
如上图所示,左侧是金属板工件,中间是在LED同轴光源下,均匀地照亮整个表面,因此很难探测到凸起。右侧是在LFX3线性光源下,线条图案光源将凸起突出为曲线。
机器视觉产品资料查询平台可查看更多工业光源的信息。
这篇关于简述CCS平面线性光源的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







