流形学习之拉普拉斯特征映射

本文主要是介绍流形学习之拉普拉斯特征映射，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

首先，我们说一下流形学习；接着，我们重点介绍拉普拉斯特征映射算法；最后，本文将给出拉普拉斯特征特征映射算法代码。

流形学习

流形学习是一种非线性降维方法，能够从高维数据中发现低维流形结构，得到高维和低维之间的映射关系，从而实现数据的维数约简。**为什么要实现特征约简？**因为高维的数据存在数据量大并且高维数据输入到网络模型中训练难度较大，耗费时间长。
流形学习展示图，其中包括Isomap（等距映射算法），LLP（局部保持投影），LE（拉普拉斯特征映射）等

拉普拉斯特征映射

原理

拉普拉斯特征映射是一种典型的流形学习方法，它是运用图拉普拉斯概念计算高维特征集得到低维流形表示。拉普拉斯特征映射算法降维的实质就是寻找到一个平均意义上保持数据点局部邻近信息，即在原来高维特征空间中是近邻的点在低维表示中也应该是近邻的。拉普拉斯特征映射算法所产生的映射可以看作是对几何流形的一种连续离散逼近的映射，用数据点的邻域图来近似表示流形，并用Laplace-Beltrami 算子近似表示邻域图的权值矩阵，实现高维流形的最优嵌入。这样就将问题简单转化为对拉普拉斯算子的特征函数的求解。

构建近邻图。如果Xi和Xj为近邻点，就在节点i和 j 之间置一条边，的 K 近邻域法构建近邻图，K的取值可以具体参考文献。
确定边的权值 Wij。同样边的权值确定也有两种方法:① 热核法(Heat Kernel)。若第i个和第j个节点之间是连接的，则边的权值为。

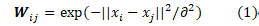
若Wij=0。如果第i个和第j个节点之间有边连接，则定义边的权值Wij=1，否则Wij=0。
3.特征映射。假设前面所建立的近邻图是连通的，那么寻找低维嵌入的问题就归结为对广义特征向量问题的求解:Ly = λDy式中：D是对角权值矩阵，它的每个元素 Dii =∑jWji；其对角元是W矩阵的列或行的和(W 为对称矩阵)，L=D－W是对称的半正定的矩阵，称为拉普拉斯矩阵，可以看作是算子函数。经过特征分解后得到的第2到第d +1 项的特征值对应的特征向量即是算法的d维输出。

拉普拉斯特征映射优点

LE方法将问题转化成对矩阵特征值的求解，不需要进行迭代计算，和其他几种流形学习算法相比，计算量和运算时间大大减少计算量。

拉普拉斯特征映射代码（matlab）

clc
clearload y12
X=y12;
if ~exist('no_dims', 'var')  %检测no_dim变量是否存在no_dims = 1;endif ~exist('k', 'var') %检测k变量是否存在k = 8;endif ~exist('sigma', 'var') %检测sigma变量是否存在sigma = 1;   %sigma为什么设为1end
%确定三个参数，no_dims,k,sigma这里全部是输入% Construct neighborhood graphdisp('Constructing neighborhood graph...');   %disp是显示每个变量的值if size(X, 1) < 2000                          %返回矩阵A所对应的行数G = squareform(pdist(X, 'euclidean'));  %pdist（x）是计算x中各对行向量的相互距离，计算欧式距离% Compute neighbourhood graph[tmp, ind] = sort(G);    %sort函数是将参量中得元素按照升序和降序排列，ind是一个大小等于size(G)得数组for i=1:size(G, 1)G(i, ind((2 + k):end, i)) = 0;  endG = sparse(double(G));   %首先先将G转化为浮点型矩阵，再将举证转化为稀疏矩阵。sparse是稀疏矩阵%稀疏矩阵的作用是便于计算量大。G = max(G, G');          %取矩阵最大的    % Make sure distance matrix is symmetric确保距离矩阵是对称的elseG = find_nn(X, k);    %K近邻求点endG = G .^ 2;        %.^2是矩阵中的每个元素都求平方G = G ./ max(max(G));% Compute weights (W = G)disp('Computing weight matrices...');    %可以直接将要显示的字符放入括号中，进行表达。% Compute Gaussian kernel (heat kernel-based weights)G(G ~= 0) = exp(-G(G ~= 0) / (2 * sigma ^ 2));     %高斯核公式% Construct diagonal weight matrixD = diag(sum(G, 2)); %构建对角权重矩阵% Compute LaplacianL = D - G;%G是邻接矩阵L(isnan(L)) = 0; D(isnan(D)) = 0;    %确定哪些数组元素为NANL(isinf(L)) = 0; D(isinf(D)) = 0;    %%返回维数与A相同的数组A中元素为正无穷、负无穷时，返回1，否则返回0%isinf()测试某个浮点数是否是无限大，其中INF表示无穷大% Construct eigenmaps (solve Ly = labda*Dy)disp('Constructing Eigenmaps...');  tol = 0;options.disp = 0;options.isreal = 1;  %确定数组是否为实数数组options.issym = 1;   %对称[mappedX, lambda] = eigs(L, D, no_dims + 1, tol, options);	%为什么是这样的  %eigs函数主要是通过迭代法来求解矩阵特征值和特征向量 		% only need bottom (no_dims + 1) eigenvectors% Sort eigenvectors in ascending orderlambda = diag(lambda); %构造对角函数[lambda, ind] = sort(lambda, 'ascend');%'ascend' 升序排列(默认)。ind表示最小的位置lambda = lambda(1:no_dims + 1);%求值% Final embeddingmappedX3 = mappedX(:,ind(2:no_dims +1));

拉普拉斯特征映射代码（python）

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits
from mpl_toolkits.mplot3d import Axes3D'''
author: heucoder
email: 812860165@qq.com
date: 2019.6.13
'''def make_swiss_roll(n_samples=100, noise=0.0, random_state=None):#Generate a swiss roll dataset.t = 1.5 * np.pi * (1 + 2 * np.random.rand(1, n_samples))x = t * np.cos(t)y = 83 * np.random.rand(1, n_samples)z = t * np.sin(t)X = np.concatenate((x, y, z))X += noise * np.random.randn(3, n_samples)X = X.Tt = np.squeeze(t)return X, tdef rbf(dist, t = 1.0):'''rbf kernel function'''return np.exp(-(dist/t))def cal_pairwise_dist(x):'''计算pairwise 距离, x是matrix(a-b)^2 = a^2 + b^2 - 2*a*b'''sum_x = np.sum(np.square(x), 1)dist = np.add(np.add(-2 * np.dot(x, x.T), sum_x).T, sum_x)#返回任意两个点之间距离的平方return distdef cal_rbf_dist(data, n_neighbors = 10, t = 1):dist = cal_pairwise_dist(data)dist[dist < 0] = 0n = dist.shape[0]rbf_dist = rbf(dist, t)W = np.zeros((n, n))for i in range(n):index_ = np.argsort(dist[i])[1:1+n_neighbors]W[i, index_] = rbf_dist[i, index_]W[index_, i] = rbf_dist[index_, i]return Wdef le(data,n_dims = 2,n_neighbors = 5, t = 1.0):''':param data: (n_samples, n_features):param n_dims: target dim:param n_neighbors: k nearest neighbors:param t: a param for rbf:return:'''N = data.shape[0]W = cal_rbf_dist(data, n_neighbors, t)D = np.zeros_like(W)for i in range(N):D[i,i] = np.sum(W[i])D_inv = np.linalg.inv(D)L = D - Weig_val, eig_vec = np.linalg.eig(np.dot(D_inv, L))sort_index_ = np.argsort(eig_val)eig_val = eig_val[sort_index_]print("eig_val[:10]: ", eig_val[:10])j = 0while eig_val[j] < 1e-6:j+=1print("j: ", j)sort_index_ = sort_index_[j:j+n_dims]eig_val_picked = eig_val[j:j+n_dims]print(eig_val_picked)eig_vec_picked = eig_vec[:, sort_index_]# print("L: ")# print(np.dot(np.dot(eig_vec_picked.T, L), eig_vec_picked))# print("D: ")# D not equal I ???print(np.dot(np.dot(eig_vec_picked.T, D), eig_vec_picked))X_ndim = eig_vec_pickedreturn X_ndimif __name__ == '__main__':# X, Y = make_swiss_roll(n_samples = 2000)# X_ndim = le(X, n_neighbors = 5, t = 20)## fig = plt.figure(figsize=(12,6))# ax1 = fig.add_subplot(121, projection='3d')# ax1.scatter(X[:, 0], X[:, 1], X[:, 2], c = Y)## ax2 = fig.add_subplot(122)# ax2.scatter(X_ndim[:, 0], X_ndim[:, 1], c = Y)# plt.show()X = load_digits().datay = load_digits().targetdist = cal_pairwise_dist(X)max_dist = np.max(dist)print("max_dist", max_dist)X_ndim = le(X, n_neighbors = 20, t = max_dist*0.1)plt.scatter(X_ndim[:, 0], X_ndim[:, 1], c = y)plt.savefig("LE2.png")plt.show()