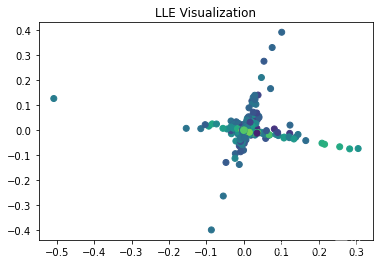
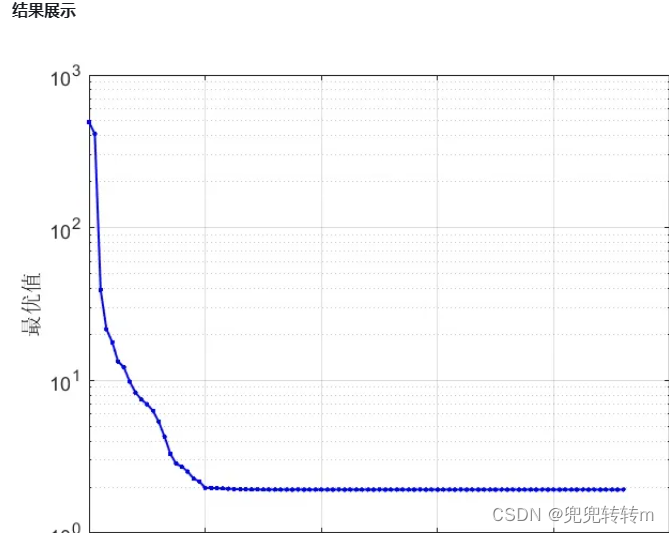
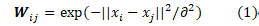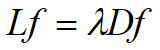流形专题

机器学习(V)--无监督学习(六)流形学习

title: 机器学习(V)–无监督学习(二)流形学习 date: katex: true categories: Artificial IntelligenceMachine Learning tags:机器学习 cover: /img/ML-unsupervised-learning.png top_img: /img/artificial-intelligence.jpg abbrli

参数搜索流形学习

目录一、网格搜索1、介绍2、代码示例二、HalvingGridSearch1、介绍2、代码示例三、随机搜索1、介绍2、代码示例三、贝叶斯搜索1、介绍2、代码示例四、参数搜索总结五、流形学习1、LLE1、介绍2、官方代码示例 2、t-SNE1、介绍2、官方代码示例一、网格搜索 1、介绍网格搜索（grid search）是一种用来选择模型超参数的方法。它通过遍历超

流形学习-Manifold Learning

来源：转载本文请联系原作者获取授权，同时请注明本文来自张重科学网博客。链接地址：http://blog.sciencenet.cn/blog-722391-583413.html 流形（manifold）的概念最早是在1854年由 Riemann 提出的(德文Mannigfaltigkeit)，现代使用的流形定义则是由 Hermann Weyl 在1913年给出的。江泽

流形学习（Manifold Learning）

基本概念 Manifold Learning（流形学习）是一种机器学习和数据分析的方法，它专注于从高维数据中发现低维的非线性结构。流形学习的基本假设是，尽管数据可能在高维空间中呈现，但它们实际上分布在一个低维的流形上。这个流形是数据的真实结构，它捕捉了数据中的内在关系和模式。流形是一个数学概念，指的是在局部类似于欧几里得空间的拓扑空间。在高维数据分析中，流形可以被看作是数据点自然聚集的低维表

超分辨率重重建——流形学习

在阅读超分辨率重建相关文献的时候，经常会见到流形学习这么个词，今天整理了一下以下内容摘自百度：http://baike.baidu.com/link?url=bt9Cv9MtYOgqGcTcT7ZJp19ezCOj-eNVVIZOru18VlkuM4Yo9jE3Tmx_NpRFJUruoxBj-5A33_Y3qviRaLaKrnWt_UJd2W0vy-c4ifvuan3CDSAHQrB9NxT

非常好的介绍流形假设文章

总觉得即使是“浅谈”两个字，还是让这个标题有些过大了，更何况我自己也才刚刚接触这么一个领域。不过懒得想其他标题了，想起来要扯一下这个话题，也是因为和朋友聊起我自己最近在做的方向。Manifold Learning 或者仅仅 Manifold 本身通常就听起来颇有些深奥的感觉，不过如果并不是想要进行严格的理论推导的话，也可以从许多直观的例子得到一些感性的认识，正好我也就借这个机会来简单地谈一下这个

[深度学习] 流形学习（未完待续）

流形学习流形学习，全称流形学习方法(Manifold Learning)，自2000年在著名的科学杂志《Science》被首次提出以来，已成为信息科学领域的研究热点。假设数据是均匀采样于一个高维欧氏空间中的低维流形，流形学习就是从高维采样数据中恢复低维流形结构，即找到高维空间中的低维流形，并求出相应的嵌入映射，以实现维数约简或者数据可视化。它是从观测到的现象中去寻找事物的本质，找到产生数据

使用离散化终端流形的时间临界街道场景的最优轨迹

Optimal trajectories for time-critical street scenarios using discretized terminal manifolds 流形空间：流形是局部具有欧几里得空间性质的空间，在数学中用于描述几何形体 semi-reactive planning strategy：半反应规划策略 maneuver tasks：机动任务 lane-

【声源定位】基于matlab阵列流形矩阵信号显示【含Matlab源码 549期】

⛄一、获取代码方式获取代码方式1：完整代码已上传我的资源：【声源定位】基于matlab阵列流形矩阵信号显示【含Matlab源码 549期】点击上面蓝色字体，直接付费下载，即可。获取代码方式2：付费专栏Matlab语音处理（初级版）备注：点击上面蓝色字体付费专栏Matlab语音处理（初级版），扫描上面二维码，付费29.9元订阅海神之光博客付费专栏Matlab语音处理（初级版），凭

【三维视觉】TetWild / fTetWild学习：将任意mesh处理成流形水密的mesh

项目地址 TetWild - Tetrahedral Meshing in the Wild 快速版本：Fast Tetrahedral Meshing in the Wild 2D版本： TriWild: Robust Triangulation With Curve Constraints 快速版本的fTetWild 输入与输出输入：任意网格：.off/.obj/.stl/.ply

$流形和图形的关系$

流形和图形的关系

搬运学习一篇arkiv文章《The Mathematical Foundations of Manifold Learning》，主要介绍流形和图的关系。文章doi: https://doi.org/10.48550/arXiv.2011.01307 乍一看这两个数学概念似乎并不相似，因为图一般研究其组合性质，流形一般研究其拓扑和几何性质。然而，这两个概念存在深刻

流形学习之拉普拉斯特征映射

首先，我们说一下流形学习；接着，我们重点介绍拉普拉斯特征映射算法；最后，本文将给出拉普拉斯特征特征映射算法代码。流形学习流形学习是一种非线性降维方法，能够从高维数据中发现低维流形结构，得到高维和低维之间的映射关系，从而实现数据的维数约简。**为什么要实现特征约简？**因为高维的数据存在数据量大并且高维数据输入到网络模型中训练难度较大，耗费时间长。流形学习展示图，其中包括Isomap（等距

林浩然的流形漫游与微分几何奇遇记

林浩然的流形漫游与微分几何奇遇记 Lin Haoran’s Manifold Odyssey and Adventures in Differential Geometry 在数学王国的另一片疆域，我们的主人公林浩然是一位热衷于探索未知世界的冒险家。这一次，他将带领我们穿越到神秘的“流形世界”，并在这个奇妙的舞台上，演绎一场融合了拓扑、微积分和几何的幽默大戏。 In anothe

机器学习——流形学习

流形学习是一种在机器学习领域中用于理解和分析数据的技术。它的核心思想是，尽管我们通常将数据表示为高维空间中的向量，但实际上数据可能具有较低维度的内在结构，这种结构被称为流形。流形学习的目标是发现并利用数据的这种潜在结构，以便更好地理解和处理数据。一些基本概念开始： 1. 流形流形是一种数学概念，指的是局部类似于欧几里德空间的空间。简单来说，流形可以理解为在高维空间中弯曲或扭曲的低维子空间

西瓜书学习笔记——流形学习（公式推导+举例应用）

文章目录等度量映射（仅保留点与其邻近点的距离）算法介绍实验分析局部线性嵌入（不仅保留点与其邻近点的距离还要保留邻近关系）算法介绍实验分析等度量映射（仅保留点与其邻近点的距离）算法介绍等度量映射（Isomap）的基本思想是通过保持数据点之间的测地距离（沿着数据流形的最短路径测量的距离）来近似保持数据流形的局部几何结构。这与传统的多维缩放（MDS）不同，MDS通常保

第十二届“中关村青联杯”全国研究生数学建模竞赛-B题：数据的多流形结构分析(续)

目录 5.3.2 问题 2 求解 5.4 结果分析 6 问题 3 模型的建立与求解 6.1 问题 3 重述

智能反射面—流形优化

使用Manopt工具箱适合优化最小化问题，如果你的优化问题是最大化问题，那么需要将其转换为最小化问题然后使用Manopt工具箱求解。具体安装过程 Matlab添加Manopt - 知乎 (zhihu.com) 优化问题 clc,clear;close all;s=rng(1);%rand seedN=10;GR_num=1e3;% number, should be

机器学习---流形学习

1. 流形学习作为机器学习研究的热点问题之一，流形学习是要从高维数据集中发现内在的低维流形，并基于低维流形来实现随后的各种机器学习任务，如模式识别，聚类分析。与欧氏空间不同，流形学习主要处理的是非欧空间里的模式识别和维数约简等问题。从宇宙空间看地球，如果不借助外界力量的话，我们只能局限于地球的表面活动，而且地球上两点的距离并不单纯是它们对应的直线的跟离，而是测地线距离。可以证明

浅谈流形学习（转）

http://blog.pluskid.org/?p=533 总觉得即使是“浅谈”两个字，还是让这个标题有些过大了，更何况我自己也才刚刚接触这么一个领域。不过懒得想其他标题了，想起来要扯一下这个话题，也是因为和朋友聊起我自己最近在做的方向。Manifold Learning 或者仅仅 Manifold 本身通常就听起来颇有些深奥的感觉，不过如果并不是想要进行严格的理论推导的话，也可以从许多直观的

“华为杯”研究生数学建模竞赛2015年-【华为杯】B题：数据的多流形结构分析（续）（附python代码实现））

目录 6.3 问题三求解 6.3.1 题 a 求解 6.3.2 题 b 求解 6.3.3 题 c 求解 6.4 问题四求解 6.4.1 图