西瓜书学习笔记——流形学习（公式推导+举例应用）

本文主要是介绍西瓜书学习笔记——流形学习（公式推导+举例应用），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

等度量映射（仅保留点与其邻近点的距离）

算法介绍

等度量映射（Isomap）的基本思想是通过保持数据点之间的测地距离（沿着数据流形的最短路径测量的距离）来近似保持数据流形的局部几何结构。这与传统的多维缩放（MDS）不同，MDS通常保持点之间的欧几里德距离，而这可能在流形结构下失效。

而流形是指在高维空间中嵌入的低维结构，这种结构可能是非线性的、弯曲的，而不是简单的线性关系。

接着利用流行在局部上与欧式空间同胚这个性质，对每个点基于欧式距离找出其近邻点，然后将近邻点连接起来，构成一个无向图，接着使用Dijkstra或Floyd求解最短路径构成距离矩阵，最终使用MDS算法求解。

其中同胚是指，一个$n$维流形是指每个点都有一个邻域，该邻域与$n$维欧式空间中的开集同胚。这意味着在每个点的附近，流形的局部结构可以用欧式空间的坐标系统来描述。虽然整个流形可能是非欧式的，但在每个点处，我们可以找到一个局部的坐标系统，使得该点附近的结构与欧式空间中的结构相似。（这与微积分的定义很相似，都是在某一邻域上的近似）

下图是Isomap的算法流程图：

Isomap 只提供了训练样本在低维空间的坐标，对于新样本，一种通用的方法是使用回归学习器。通过将训练样本的高维空间坐标作为输入，相应的低维空间坐标作为输出，训练一个回归模型。该模型可用于对新样本的低维空间坐标进行预测，尽管这只是一种权宜之计，目前似乎还没有更好的方法来处理 Isomap 在新样本上的映射问题。

构建近邻图有两种常见方法：一是指定K近邻点，二是指定距离阈值得到d近邻图。但两者存在问题，过大的近邻范围可能导致“短路”，将远距离点误认为近邻；反之，过小的范围可能导致“断路”，某些区域与其他区域失去连接。这可能对后续最短路径计算产生误导。选择构建方法时需要权衡参数以避免这些问题。

实验分析

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt# 读取数据
data = pd.read_csv('data/correlated_dataset.csv')# 计算欧氏距离
def euclidean_distance(point1, point2):return np.sqrt(np.sum((point1 - point2)**2))# 计算近邻图
def compute_neighbors(data, k=5):num_samples = len(data)neighbors = np.zeros((num_samples, k), dtype=int)for i in range(num_samples):distances = [euclidean_distance(data.iloc[i], data.iloc[j]) for j in range(num_samples) if i != j]indices = np.argsort(distances)[:k]neighbors[i] = indicesreturn neighbors# 计算测地距离
def compute_geodesic_distances(neighbors, data):num_samples = len(data)geodesic_distances = np.zeros((num_samples, num_samples))for i in range(num_samples):for j in range(num_samples):if i != j:path_distance = 0current = inext_neighbor = neighbors[i, 0]while next_neighbor != j:path_distance += euclidean_distance(data.iloc[current], data.iloc[next_neighbor])current = next_neighbornext_neighbor = neighbors[current, 0]geodesic_distances[i, j] = path_distancereturn geodesic_distances# Isomap算法
def isomap(data, k_neighbors=5, low_dim=2):# 计算近邻图neighbors = compute_neighbors(data, k_neighbors)# 计算测地距离geodesic_distances = compute_geodesic_distances(neighbors, data)# 使用MDS算法降维n = len(data)H = np.eye(n) - np.ones((n, n)) / nB = -0.5 * H @ geodesic_distances**2 @ Heigvals, eigvecs = np.linalg.eigh(B)# 取最小的low_dim个特征值对应的特征向量indices = np.argsort(eigvals)[:low_dim]low_dim_eigvecs = eigvecs[:, indices]return low_dim_eigvecs# 降维
low_dim_data = isomap(data.drop(columns=['Target']))# 可视化降维结果
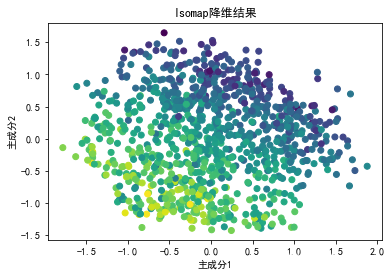
plt.scatter(low_dim_data[:, 0], low_dim_data[:, 1], c=data['Target'], cmap='viridis')
plt.title('Isomap降维结果')
plt.xlabel('主成分1')
plt.ylabel('主成分2')
plt.show()

局部线性嵌入（不仅保留点与其邻近点的距离还要保留邻近关系）

算法介绍

与Isomap算法不同，局部线性嵌入（LLE）算法是要保留邻近关系。

如下图所示：

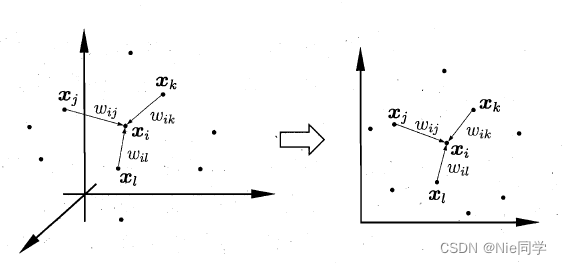
假定样本点$x_i$的坐标能通过它的领域内的样本$x_j,x_k,x_l$的坐标通过线性组合而重构出来的，即：

$$x_i=w_{ij}{x}_j+w_{ik}{x}_k+w_{il}{x}_l\text{\hspace{1em}(1)}$$

而LLE算法希望式（1）这种关系能在低维空间中依然存在。

LLE算法先对每个样本$x_i$找出其近邻的下标集合$Q_i$，然后计算出基于$Q_i$中的样本点对$x_i$进行线性重构的系数$w_i$：
$$\begin{array}{rl}\underset{{\mathbf{w}}_1,{\mathbf{w}}_2,\dots ,{\mathbf{w}}_m}{\min }& \sum _{i=1}^m{\Vert {\mathbf{x}}_i-\sum _{j\in Q_i}{w}_{ij}{\mathbf{x}}_j\Vert }_2^2\\ \text{ s.t. }& \sum _{j\in Q_i}{w}_{ij}=1\end{array}\text{\hspace{1em}(2)}$$

我们可以将式（2）进行恒等变形：

$$\begin{array}{rl}\sum _{i=1}^m{\Vert {\mathbf{x}}_{\mathbf{i}}-\sum _{j\in Q_i}{w}_{ij}{\mathbf{x}}_j\Vert }_2^2& =\sum _{i=1}^m{\Vert \sum _{j\in Q_i}{w}_{ij}{\mathbf{x}}_i-\sum _{j\in Q_i}{w}_{ij}{\mathbf{x}}_j\Vert }_2^2\\ & =\sum _{i=1}^m{\Vert \sum _{j\in Q_i}{w}_{ij}\left({\mathbf{x}}_i-{\mathbf{x}}_j\right)\Vert }_2^2\\ & =\sum _{i=1}^m{\Vert {\mathbf{X}}_i{\mathbf{w}}_{\mathbf{i}}\Vert }_2^2\\ & =\sum _{i=1}^m{\mathbf{w}}_{\mathbf{i}}{}^{\mathrm{T}}{\mathbf{X}}_i^{\mathrm{T}}{\mathbf{X}}_i{\mathbf{w}}_{\mathbf{i}}\end{array}\text{\hspace{1em}(3)}$$

其中${\mathbf{w}}_{\mathbf{i}}=\left(w_{i{q}_i^1},w_{i{q}_i^2},\dots ,w_{i{q}_i^n}\right)\in {\mathbb{R}}^{n\times 1},{\mathbf{X}}_i=\left({\mathbf{x}}_i-{\mathbf{x}}_{q_i^1},{\mathbf{x}}_i-{\mathbf{x}}_{q_i^2},\dots ,{\mathbf{x}}_i-{\mathbf{x}}_{q_i^n}\right)\in {\mathbb{R}}^{d\times n}$。约束条件可进行如下恒等变形：

$$\sum _{j\in Q_i}{w}_{ij}=w_i^T\mathbf{E}=1\text{\hspace{1em}(4)}$$

其中$\mathbf{E}=(1,1,...,1)\in {\mathbb{R}}^{n\times 1}$为$n$行1列的单位向量。

故优化问题可重写成：
$$\begin{array}{rl}\underset{{\mathbf{w}}_1,{\mathbf{w}}_2,\dots ,{\mathbf{w}}_m}{\min }& \sum _{i=1}^m{\mathbf{w}}_{\mathbf{i}}{}^{\mathrm{T}}{\mathbf{X}}_i^{\mathrm{T}}{\mathbf{X}}_i{\mathbf{w}}_{\mathbf{i}}\\ \text{ s.t. }& w_i^T\mathbf{E}=1\end{array}\text{\hspace{1em}(5)}$$

采用拉格朗日乘子法求解，有：

$$L\left({\mathbf{w}}_1,{\mathbf{w}}_2,\dots ,{\mathbf{w}}_m,\lambda \right)=\sum _{i=1}^m{\mathbf{w}}_{\mathbf{i}}^{\mathrm{T}}{\mathbf{X}}_i^{\mathrm{T}}{\mathbf{X}}_i{\mathbf{w}}_{\mathbf{i}}+\lambda \left({\mathbf{w}}_{\mathbf{i}}^{\mathrm{T}}\mathbf{E}-1\right)\text{\hspace{1em}(6)}$$

式（6）对$w_i$求偏导并令其为零，有：
$$\frac{\partial L}{\partial w_i}=2{\mathbf{X}}_i^T{\mathbf{X}}_i{w}_i+\lambda \mathbf{E}=0\text{\hspace{1em}(8)}$$

则：

$$w_i=-\frac{1}{2}\lambda ({\mathbf{X}}_i^T{\mathbf{X}}_i{)}^{-1}\mathbf{E}\text{\hspace{1em}(9)}$$

又因为$w_i^T\mathbf{E}={\mathbf{E}}^T{w}_i=1$，故式（9）两边同时左乘${\mathbf{E}}^T$，有：

$$\begin{array}{rl}{\mathbf{E}}^T{w}_i& =-\frac{1}{2}\lambda {\mathbf{E}}^T({\mathbf{X}}_i^T{\mathbf{X}}_i{)}^{-1}\mathbf{E}\\ -\frac{1}{2}\lambda & =\frac{1}{{\mathbf{E}}^T({\mathbf{X}}_i^T{\mathbf{X}}_i{)}^{-1}\mathbf{E}}\end{array}\text{\hspace{1em}(10)}$$

然后回代入式（9）中，有：

$$w_i=\frac{({\mathbf{X}}_i^T{\mathbf{X}}_i{)}^{-1}\mathbf{E}}{{\mathbf{E}}^T({\mathbf{X}}_i^T{\mathbf{X}}_i{)}^{-1}\mathbf{E}}\text{\hspace{1em}(11)}$$

令矩阵$({\mathbf{X}}_i^T{\mathbf{X}}_i{)}^{-1}$第$i$行第$k$列的元素为$C_{jk}^{-1}$，即$C_{jk}=(x_i-x_j{)}^T(x_i-x_j)$，则：

$$w_{ij}=w_{i{q}_i^j}=\frac{{\sum }_{k\in Q_i}{C}_{jk}^{-1}}{{\sum }_{l,s\in Q_i}{C}_{ls}^{-1}}\text{\hspace{1em}(12)}$$

其中$w_{ij}$原始数据集中的某个数据点 ${\mathbf{x}}_i$的邻近集合$Q_i$中的某个邻居点 ${\mathbf{x}}_j$对重构${\mathbf{x}}_i$的权重。

由于LLE在低维空间中保持$w_i$不变，于是$x_i$对应的低维空间坐标$z_i$可通过下式求解：

$$\begin{array}{rl}\underset{{\mathbf{w}}_1,{\mathbf{w}}_2,\dots ,{\mathbf{w}}_m}{\min }& \sum _{i=1}^m{\Vert {\mathbf{z}}_i-\sum _{j\in Q_i}{w}_{ij}{\mathbf{z}}_j\Vert }_2^2\end{array}\text{\hspace{1em}(13)}$$

令$\mathbf{Z}=\left({\mathbf{z}}_1,{\mathbf{z}}_2,\dots ,{\mathbf{z}}_m\right)\in {\mathbb{R}}^{d^{\prime }\times m},(\mathbf{W}{)}_{ij}=w_{ij}$。
$$\mathbf{M}=(\mathbf{E}-\mathbf{W}{)}^{\mathbf{T}}(\mathbf{E}-\mathbf{W})\text{\hspace{1em}(14)}$$

故式（13）可重写为：
$$\begin{array}{rl}\underset{\mathbf{Z}}{\min }\sum _{i=1}^m{\Vert {\mathbf{z}}_i-\sum _{j\in Q_i}{w}_{ij}{\mathbf{z}}_j\Vert }_2^2& =\sum _{i=1}^m{\Vert \mathbf{Z}{\mathbf{E}}_i-\mathbf{Z}{\mathbf{W}}_i\Vert }_2^2\\ & =\sum _{i=1}^m{\Vert \mathbf{Z}\left({\mathbf{E}}_i-{\mathbf{W}}_i\right)\Vert }_2^2\\ & =\sum _{i=1}^m{\left(\mathbf{Z}\left({\mathbf{E}}_i-{\mathbf{W}}_i\right)\right)}^T\mathbf{Z}\left({\mathbf{E}}_i-{\mathbf{W}}_i\right)\\ & =\sum _{i=1}^m{\left({\mathbf{E}}_i-{\mathbf{W}}_i\right)}^T{\mathbf{Z}}^T\mathbf{Z}\left({\mathbf{E}}_i-{\mathbf{W}}_i\right)\\ & =\mathrm{tr}\left((\mathbf{E}-\mathbf{W}{)}^T{\mathbf{Z}}^T\mathbf{Z}(\mathbf{E}-\mathbf{W})\right)\\ & =\mathrm{tr}\left(\mathbf{Z}(\mathbf{E}-\mathbf{W})(\mathbf{E}-\mathbf{W}{)}^T{\mathbf{Z}}^T\right)\\ & =\mathrm{tr}\left(\mathbf{Z}\mathbf{M}{\mathbf{Z}}^T\right)\end{array}\text{\hspace{1em}(15)}$$

其约束条件为${\mathbf{Z}}^{\mathbf{T}}\mathbf{Z}=\mathbf{E}$是为了得到标准化的低维数据。

整理一下可得：

$$\begin{array}{rl}\underset{\mathbf{Z}}{\min }& \mathrm{tr}\left(\mathbf{Z}\mathbf{M}{\mathbf{Z}}^T\right)\\ \text{ s.t. }& {\mathbf{Z}}^{\mathbf{T}}\mathbf{Z}=\mathbf{E}\end{array}\text{\hspace{1em}(16)}$$

最终可通过对$\mathbf{M}$进行特征值分解，取$\mathbf{M}$最小的$d^{\prime }$个特征值所对应的特征向量组成的矩阵即为${\mathbf{Z}}^{\mathbf{T}}$。

LLE算法流程图如下所示：

实验分析

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt# 读取数据
data = pd.read_csv('data/correlated_dataset.csv')# LLE算法实现
def lle(X, n_neighbors, n_components):m, d = X.shapeW = np.zeros((m, m))# Step 1: 选择近邻for i in range(m):indices = find_neighbors(X[i], X, n_neighbors)W[i, indices] = compute_weights(X[i], X[indices], indices)# Step 2: 计算低维表示M = np.identity(m) - Weigenvalues, eigenvectors = np.linalg.eigh(M)idx = np.argsort(eigenvalues)[1:n_components + 1]embedding = eigenvectors[:, idx]return embedding# 找到近邻
def find_neighbors(x, X, n_neighbors):distances = np.linalg.norm(X - x, axis=1)indices = np.argsort(distances)[:n_neighbors]return indices# 计算权重
def compute_weights(x, X, indices):Z = X - xC = Z @ Z.Tones = np.ones(len(indices))w = np.linalg.solve(C + 1e-3 * np.identity(len(indices)), ones)w /= np.sum(w)return w# 降维并可视化
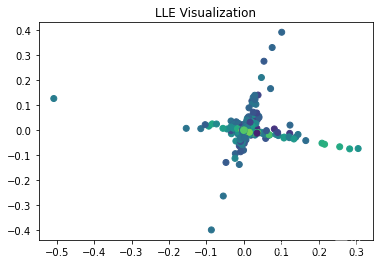
embedding = lle(data.values[:, :-1], n_neighbors=10, n_components=2)plt.scatter(embedding[:, 0], embedding[:, 1], c=data['Target'], cmap='viridis')
plt.title('LLE Visualization')
plt.show()

这篇关于西瓜书学习笔记——流形学习（公式推导+举例应用）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---