本文主要是介绍智能反射面—流形优化,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
使用Manopt工具箱适合优化最小化问题,如果你的优化问题是最大化问题,那么需要将其转换为最小化问题然后使用Manopt工具箱求解。
具体安装过程
Matlab添加Manopt - 知乎 (zhihu.com)
优化问题

clc,clear;
close all;
s=rng(1);%rand seed
N=10;
GR_num=1e3;% number, should be large enough
A = rand(N)+1i*rand(N);
A = (A*A'); % semidefinite matrix% SDR
cvx_begin
variable X(N,N) hermitian semidefinite
minimize (real(trace(A*X)))
subject todiag(X)==ones(N,1);cvx_end% gassian random
obj = zeros(GR_num,1);
v=zeros(N,GR_num);
[V1,D1]=eig(X);
for ii=1:GR_numv(:,ii) = V1*D1^(1/2)*sqrt(1/2)*(randn(N,1) + 1i*randn(N,1));v(:,ii) = exp(1i*angle(v(:,ii)));% guarantee constant modulusobj(ii)=real(trace(A*(v(:,ii)*v(:,ii)')));
end
[~,idx] = min(obj);
v_opt = v(:,idx);
% check constant modulus
abs(v_opt)
% check optimal value
real(cvx_optval)real(trace(v_opt'*A*v_opt ))%采用方法二进行求解
% Create the problem structure.
v_init = ones(N,1);
manifold = complexcirclefactory(N);
problem.M = manifold;
options.verbosity=0;
% Define the problem cost function and its Euclidean gradient.
problem.cost = @(x) trace(x'*A*x);
problem.egrad = @(x) 2*A*x; % notice the 'e' in 'egrad' for Euclidean% Solve.
[x, xcost, info, options] = conjugategradient(problem,v_init,options);% Display some statistics.
figure;
semilogy([info.iter], [info.gradnorm], '.-','linewidth',1);
xlabel('Iteration number');
ylabel('Norm of the gradient of f');
grid onfigure;
semilogy([info.iter], real([info.cost]), 'b.-','linewidth',1.2);
xlabel('Iteration number');
ylabel('cost');
grid on
set(gca,'fontsize',11);real(x'*A*x) 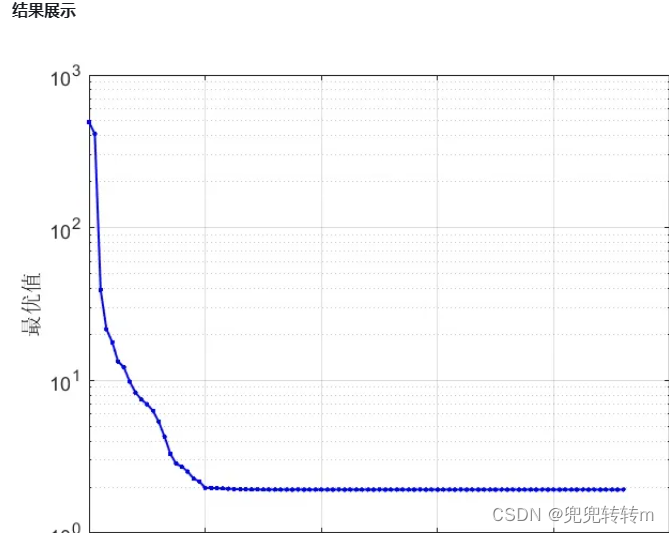
这篇关于智能反射面—流形优化的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



