本文主要是介绍信号系统之拉普拉斯变换,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
拉普拉斯变换是一种在信号连续时分析的技术。 z 变换是离散情况下使用的技术。
1 s-Domain的本质
拉普拉斯变换是一种成熟的用于求解微分方程的数学技术。与所有变换一样,拉普拉斯变换根据一组固定的规则或方程将一个信号变为另一个信号。
如图32-1所示,拉普拉斯变换将时域信号变为s域信号,也称为s-plane。时域信号是连续的,延伸到正无穷大和负无穷大,并且可以是周期性的或非周期性的。拉普拉斯变换允许时域变成复数。
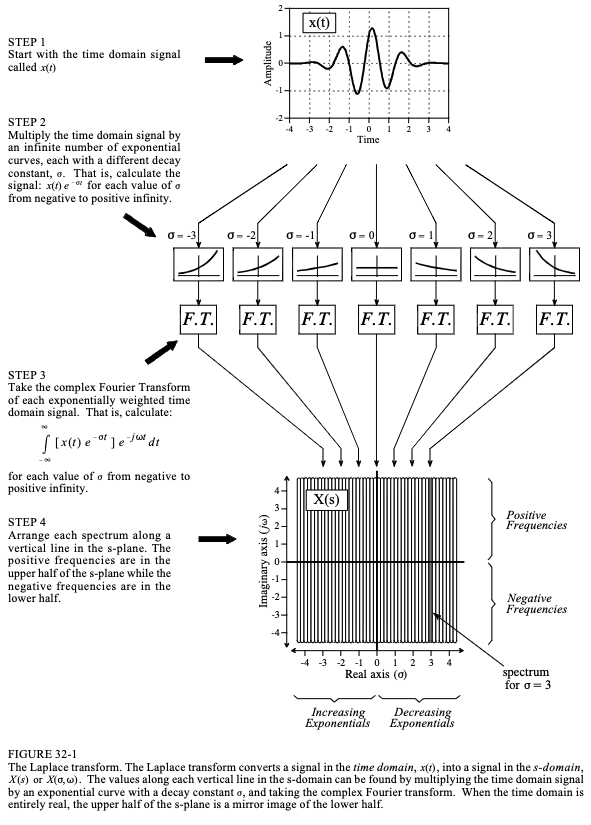
如图32-1所示,s域是一个复平面,即横轴有实数,纵轴有虚数。沿实轴的距离由变量 σ \sigma σ 表示。同样,虚轴使用变量 ω \omega ω,即固有频率。该坐标系允许通过提供 σ \sigma σ 和 ω \omega ω 的值来指定任何点的位置。使用复数表示法,每个位置都由复数变量 s 表示,其中: s = σ + ω j s=\sigma+\omega j s=σ+ωj 。
通过傅立叶变换,s 域中的信号用大写字母表示。例如,时域信号x(t) 被变换为 s域信号X(t) 或者 X ( σ , ω ) X(\sigma,\omega) X(σ,ω)。 s 平面是连续的,并且四个方向延伸至无穷。
除了具有由复数定义的位置之外,s 域中的每个点还具有一个复数值。换句话说,s 平面中的每个位置都有实部和虚部。与所有复数一样,实部和虚部也可以表示为幅度和相位。
正如傅里叶变换根据正弦曲线分析信号一样,拉普拉斯变换根据正弦曲线和指数分析信号。从数学的角度来看,这使得傅里叶变换成为更复杂的拉普拉斯变换的子集。图 32-1 显示了 s 域与时域的关系的图形描述。为了找到沿 s 平面垂直线的值(特定 σ \sigma σ处的值),时域信号首先乘以指数曲线: e − σ t e^{-\sigma t} e−σt 。 s 平面的左半部分将时域乘以随时间( σ < 0 \sigma<0 σ<0)增加的指数,右半部分乘以随时间( σ > 0 \sigma>0 σ>0)域递减的指数加。
接下来是信号的加权复傅立叶变换。所得频谱沿 s 平面中的垂直线放置,s 平面的上半部分包含正频率,下半部分包含负频率。请特别注意,s 平面( σ = 0 \sigma=0 σ=0)的 y 轴上的值恰好等于时域傅立叶信号。
复数傅立叶变换由下式给出:
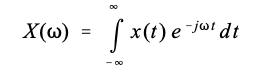
通过首先将时域信号乘以指数项,可以将其扩展为拉普拉斯变换:
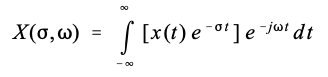
虽然这不是拉普拉斯变换的最简单形式,但它可能是对该技术的策略和操作的最佳描述。
可以将两个指数合并进行简化:
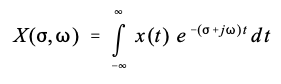
最后,复平面中的位置可以用复变量 s 表示,其中 s = σ + ω j s=\sigma+\omega j s=σ+ωj。这使得方程可以简化为更紧凑的表达:

这是拉普拉斯变换的最终形式,拉普拉斯变换是信号处理和电子学中最重要的方程之一。请特别注意术语: e − s t e^{-st} e−st ,称为复指数,如上式所示。
通过以上推导,复指数是在单个表达式中表示正弦曲线和指数的紧凑方式。
拉普拉斯变换解释为一个两阶段过程(乘以指数曲线,然后进行傅立叶变换)。
式32-1 分解为更简单的组件。拉普拉斯变换是与 x (t) 和 X(s)相关的单个方程,而不是分步过程。公式 32-1 描述了基于 σ , ω \sigma,\omega σ,ω和时域信号x(t)如何计算s平面中的每个点。
图 32-2 显示了 s 平面上的三对点:A&A’、B&B’ 和 C&C’。正如在复频谱中一样,A、B 和 C(正频率)处的点是 A’、B’ 和 C’(负频率)处的点的复共轭。 s 平面的上半部分是下半部分的镜像,并且两半部分都需要与实数时域信号相对应。换句话说,成对处理这些点可以绕过复杂的数学运算,使我们能够仅使用实数在时域中进行操作。
s 平面中每个位置的值由实部和虚部组成。将时域信号乘以指数加权余弦波,然后从 − ∞ -\infty −∞到 + ∞ +\infty +∞积分即可得到实部。虚部的计算方法相同,只是使用指数加权正弦波。方程形式如下,以 A&A’ 的实部为例:
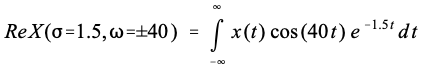
图 32-3 显示了时域波形、频谱及其 s 域表示的示例。示例时域信号是宽度为 2、高度为 1 的矩形脉冲。如图所示,该信号的复数傅立叶变换在实部是一个sinc函数,在虚部是一个完全为零的信号。 s 域是波动的二维信号,此处显示为实部和虚部的地形表面。数学原理是这样的:
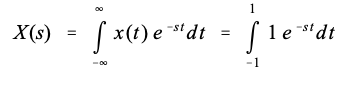
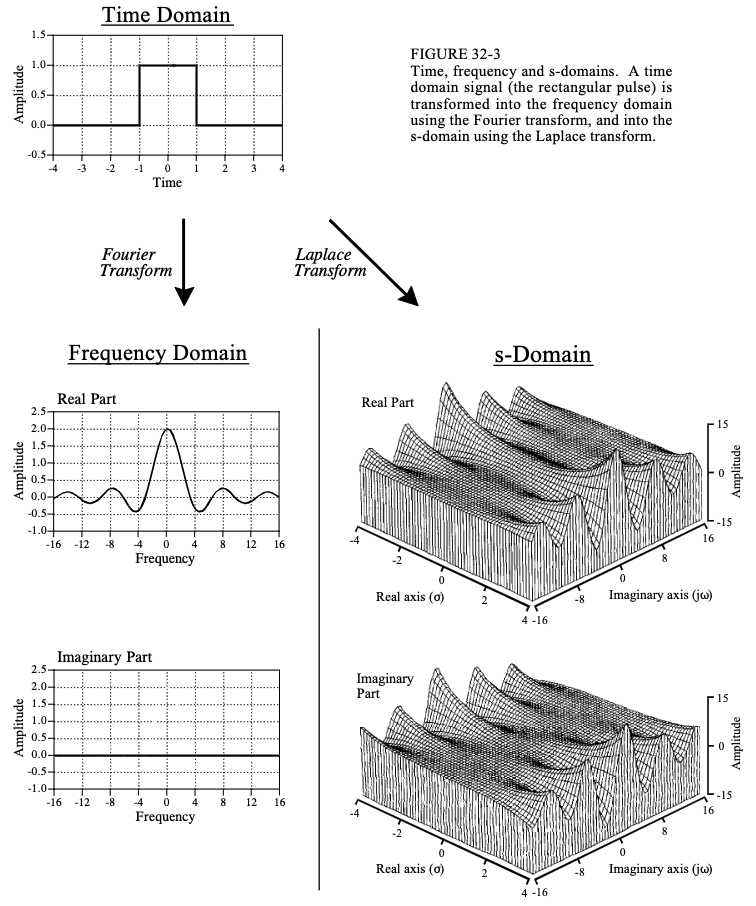
换句话说,从拉普拉斯变换(方程 32-1)的定义开始,代入x(t) 的单位值,并更改限制以匹配时域信号的非零部分。计算该积分可提供 s 域信号,以复数位置 s 和复数值 X(s) 表示:
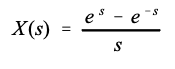
虽然这是答案最紧凑的形式,但复杂变量的使用使其难以理解,并且无法生成可视化显示,如图 32-3 所示。解决方案是将复数变量 s 替换为 σ + j ω \sigma+j \omega σ+jω,然后将实部和虚部分开:
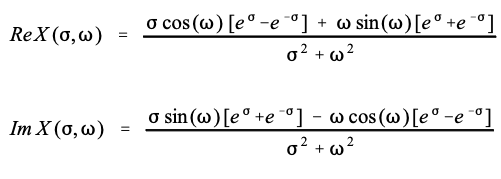
这些方程简化为沿 y 轴的傅里叶变换。这是通过将方程设置为零并简化来完成的:
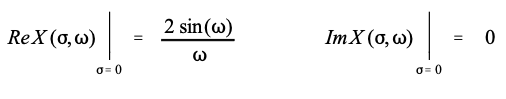
如图32-3所示,这些是正确的频域信号,与直接对时域波形进行傅里叶变换得到的结果相同。
2 拉普拉斯变换的策略
回顾图 32-3,并问:这个 s 域的形状如何帮助理解频率响应? 答案是,没有!此示例中的 s 平面构成了一个很好的图形,但它没有提供有关频域为何如此表现的见解。这是因为拉普拉斯变换旨在分析特定类别的时域信号:由正弦曲线和指数组成的脉冲响应。如果对其他波形(例如图32-3中的矩形脉冲)进行拉普拉斯变换,则得到的s域没有意义。
属于此类的系统在科学和工程中极为常见。这是因为正弦曲线和指数是微分方程的解,微分方程是控制我们物理世界大部分的数学。例如,以下所有系统都受微分方程控制:电路、波传播、线性和旋转运动、电场和磁场、热流等。
脉冲响应的特点:
- 必须具有零值,直到输入在 t=0 处变为非零。
- 它将由正弦曲线和指数组成,因为它们是控制系统的微分方程的解。
- 脉冲响应的长度将是无限的。也就是说,它具有从 t=0 到 t= + ∞ +\infty +∞ 的非零值。这是因为正弦波和余弦波的振幅是常数,而指数函数会随时间减少至零但永远不会真正达到零。如果要研究的系统是稳定的,那么随着时间的增加,冲激响应的振幅会变得更小,在时间达到无穷大时其值会变为零。此外,也存在系统不稳定的情况,例如,由于反馈过多而自发振荡的放大器。在这种情况下,冲激响应的振幅会随时间增加而增大,变得无穷大。甚至对系统的最小干扰也会产生无界的输出。
拉普拉斯变换的一般数学与傅立叶变换的数学非常相似。在这两种情况下,预定波形都乘以时域信号,并对结果进行积分。乍一看,拉普拉斯变换的策略与傅立叶变换相同:将时域信号与一组基函数相关联以分解波形。不对!尽管数学原理非常相似,但这两种技术背后的基本原理却截然不同。拉普拉斯变换探测时域波形以确定其关键特征:正弦曲线的频率和指数的衰减常数。一个例子将展示它是如何工作的。
图 32-5 中的中心列显示了 RLC 陷波滤波器的脉冲响应。它包含 t=0 处的脉冲,随后是呈指数衰减的正弦曲线。如 (a) 至 (e) 所示,将使用各种指数衰减正弦曲线来探测该脉冲响应。每个探测波形都有两个参数: ω \omega ω(确定正弦频率)和 σ \sigma σ(确定衰减率)。换句话说,每个探测波形对应于s平面上的不同位置,如图32-4中的s平面图所示。通过将脉冲响应与这些波形相乘,然后对 t = − ∞ t=-\infty t=−∞ 到 t = + ∞ t=+\infty t=+∞的结果进行积分来探测脉冲响应。此操作显示在右栏中。
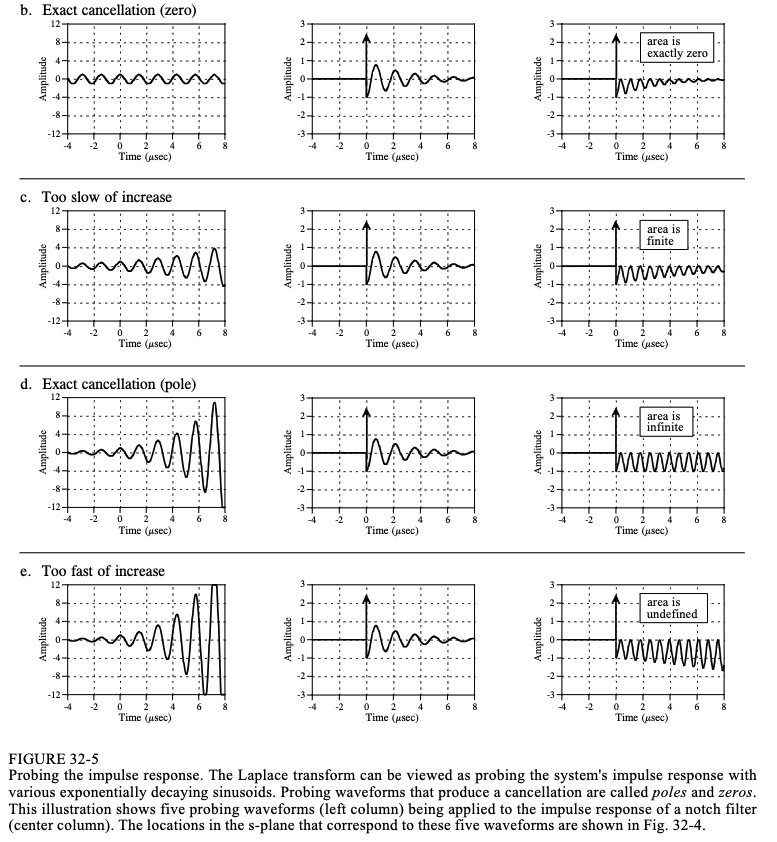
我们的目标是找到 ω \omega ω 和 σ \sigma σ 的组合,从而完全抵消正在研究的脉冲响应。这种抵消可以以两种形式发生:曲线下的面积可以为零,也可以几乎无限。所有其他结果都可以忽略。 s 平面中产生零抵消的位置称为系统的零点。同样,产生“几乎无限”类型抵消的位置称为极点。极点和零点类似于山脉和山谷,代表频率响应“周围”的地形。
首先,考虑当探测波形的幅度随着时间的推移而减小时会发生什么,如 (a) 所示。每当 σ \sigma σ> 0 探针随着时间的增加而变小,两者的乘积也将具有相同的特性。当两个波形的乘积从负无穷大积分到正无穷大时,结果将是一些并不是特别有趣的数字。特别是,递减探针不能抵消减少的脉冲响应。这意味着一个稳定的系统不会有任何极点 。换句话说,稳定系统的所有极点仅限于 s 平面的左半部分。事实上,s 位置右半部分的极点表明系统不稳定(即脉冲响应随时间增加)。
图(b)显示了一直在寻找的特殊情况之一。当该波形乘以脉冲响应时,所得积分的值为零。发生这种情况是因为 x 轴上方的面积(来自 delta 函数)恰好等于下方的面积(来自整流正弦曲线)的值。产生这种类型的抵消的称为系统的零。如图 32-4 的 s 平面示意图所示,零点用小圆圈 (⭕️) 表示。
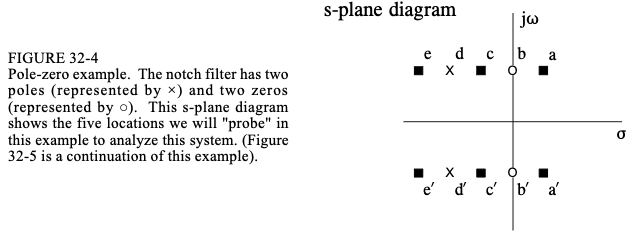
图 © 显示了可以尝试的下一个探测。在这里,使用随时间呈指数增加的正弦曲线,但其速度慢于脉冲响应随时间减少的速度。这导致两个波形的乘积也随着时间的推移而减小。如 (a) 中所示,这使得乘积的积分成为一些无趣的实数。重要的一点是不会发生任何类型的确切取消。
跳出顺序,看看 (e),探测波形的增加速度快于脉冲响应的衰减速度。相乘时,所得信号的幅度随着时间的推移而增加。这意味着曲线下的面积随着时间的增加而变大,并且总面积 t = − ∞ t=-\infty t=−∞ 到 t = + ∞ t=+\infty t=+∞收敛。换句话说,并非 s 平面的所有面积都具有定义的值。 s 平面上定义积分的部分称为收敛区域。在某些数学技术中,了解 s 平面的哪些部分位于收敛区域内非常重要。
在 (d) 中,探测波形的增加速度与脉冲响应的减少速度完全相同。这使得两个波形的乘积具有恒定的幅度。换句话说,这是 © 和 (e) 之间的分界线,导致总面积几乎未定义\。更准确地说,该点位于收敛区域的边界上。如前所述,产生这种类型的精确抵消的 ω \omega ω 和 σ \sigma σ 的值称为系统的极点。极点在 s 平面中用十字 (×) 表示。
这篇关于信号系统之拉普拉斯变换的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!