本文主要是介绍【C】快速傅里叶变换(FFT)讲解及实现,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
- 引言
- 基2FFT
1.引言
人类的求知欲是永无止境的,自1965年 T. W. Cooley 和 J. W. Tuky 在《Math. Computation, Vol, 19, 1965》发表了著名的《 An algorithm for the machine calculation of complex Fourier series 》,人们对 有关傅里叶变换的改进和创新就从未止步。1984年,P. Dohamel 和 H. Hollmann 提出的分裂基快速算法,使得算法的运算速率上升到了新台阶。
直至今日,已提出的快速算法有多种,还有很多学者在不断研究探索新的快速算法。
本文仅介绍最经典的基2FFT算法原理及编程思想。
2.基2FFT
基2FFT算法分为两类:时域抽取法FFT(Decimation-In-Time FFT, 简称 DIT - FFT);
频域抽取法FFT(Decimation-In-Frequnency FFT, 简称 DIF - FFT);
2.1 FFT 基本思想
对于信号的N点离散傅里叶变化(Discrete Fourier Transform, DFT),DFT的复乘次数为N*N, 复加次数为N*(N-1),当N = 1024时,N*N = 1048576,显然实时信号处理对时间的苛刻要求对应于当代硬件是一个矛盾。FFT算法就是不断二分DFT, 利用旋转因子W^m_N的周期性和对称性减少运算量。
周期性表现为:W^(m+iN)_N = e^( -j2*pi/N*(m+iN) ) = e^(-j2*pi/N*m - j2*pi*i) = e^(-j2*pi/N*m) = W^m_N
对称性表现为:W^(-m)_N = W^(N-m)_N or W^(m+N/2)_N = -W^m_N
2.2 时域抽取法 基FFT 基本原理
- 序列x(n)长度为16,满足N=2^M
- 将序列按照n的奇偶性二分:x(2r) and x(2r+1)
- 再二分,分到不可二分结束。
- X(k) = X1(k) + W^k_N*X2(k)
- X(k+N/2) = X1(k) + W^k_N*X2(k)
- 即 X(0) + X(0+16/2) = X(0)+X(8) = X1(0)
- X1(0)+X1(0+8/2) = X1(0)+X(4) = X2(0)
- X2(0)+X2(0+4/2) = X2(0)+X2(2) = X3(0)
- X3(0)+X3(0+2/2) = X3(0)+X3(1) = X4(0)
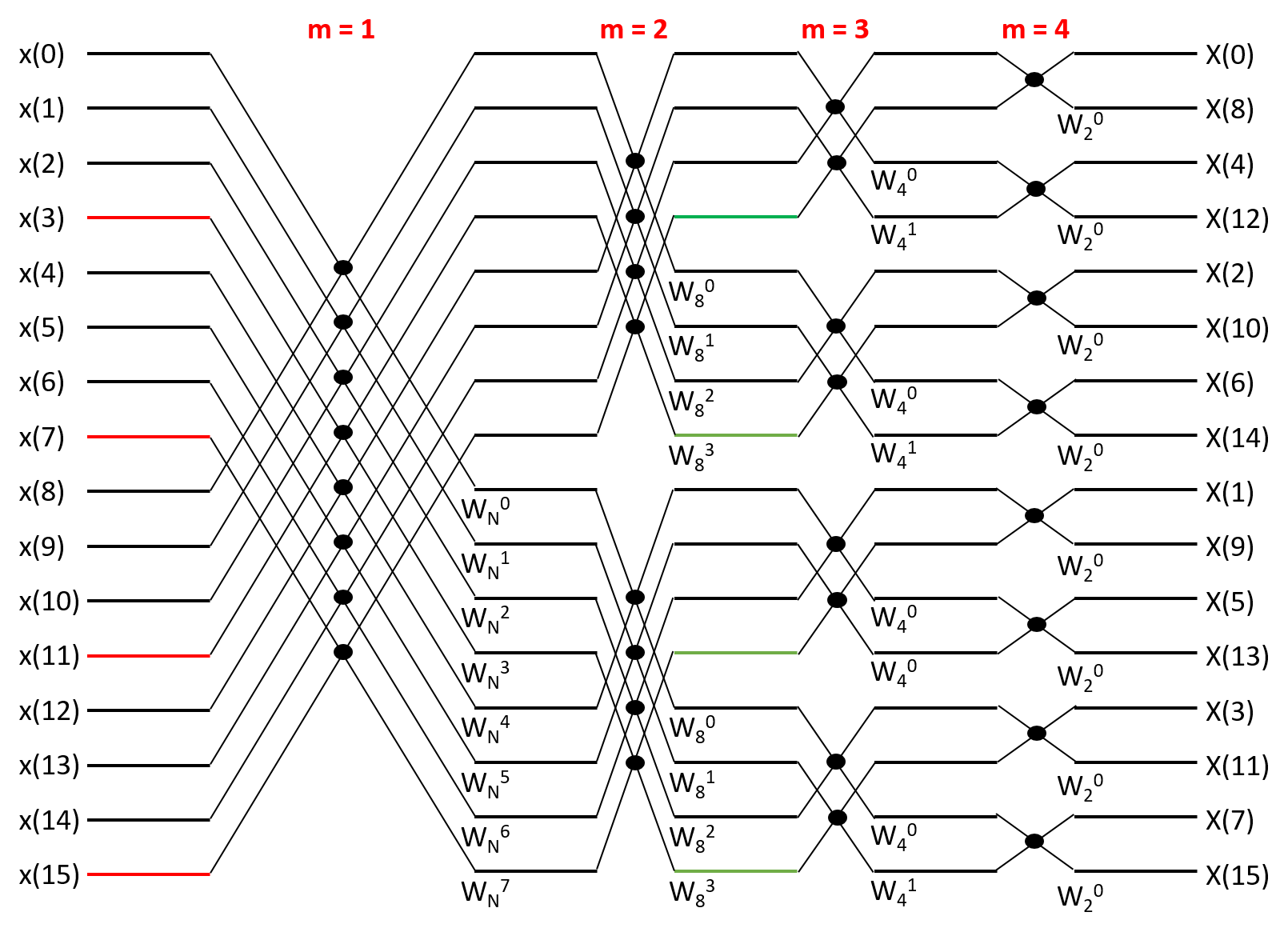
【 16点 时域抽取法FFT(简称 DIT - FFT) 】
计算量:
- 完成一次蝶形运算 = 1次复数乘法 + 两次复数加法;
- 计算1个N点DFT = 2个N/2点DFT + N/2个蝶形运算。
- 计算一个N/2点DFT = (N/2)^2次复数乘法 + (N/2)(N/2 - 1)次复数加法
- 可见,一次分解,运算量将近一半
这里附一段大神的解释【更正了其中的一些小错误】:
- 第一级,每个蝶形的两节点“距离”为1,第二级每个蝶形的两节点“距离”为2,第三级为4,第四级为8【参考上图去理解】
- 由此推得,第m级蝶形运算,每个蝶形的两节点“距离” 为 Length = 2^(m-1)
- 对于16级DIT_FFT,第一级有8组蝶形,每组一个蝶形;第二级有4个蝶形,每组两个蝶形;第三级有2个蝶形,每组四个蝶形;第四级有1个蝶形,每组有8个蝶形。
- 旋转因子W^k_N的确定
- 以16点FFT为列,第m级第k个旋转因子为
, k = 0, 1, ... ,2^m-1, 即m级共有2^m-1个旋转因子。
- 根据旋转因子的可约性,
,所以第m级第k个旋转因子为
并且,这位大神提出,为提高FFT的运算速度,我们可以建立一个旋转因子数组,然后通过查表法实现。【实际上并不实用,仅适用于确定点数且不 再修改的条件下】
//complex WN[N_series] = //旋转因子数组
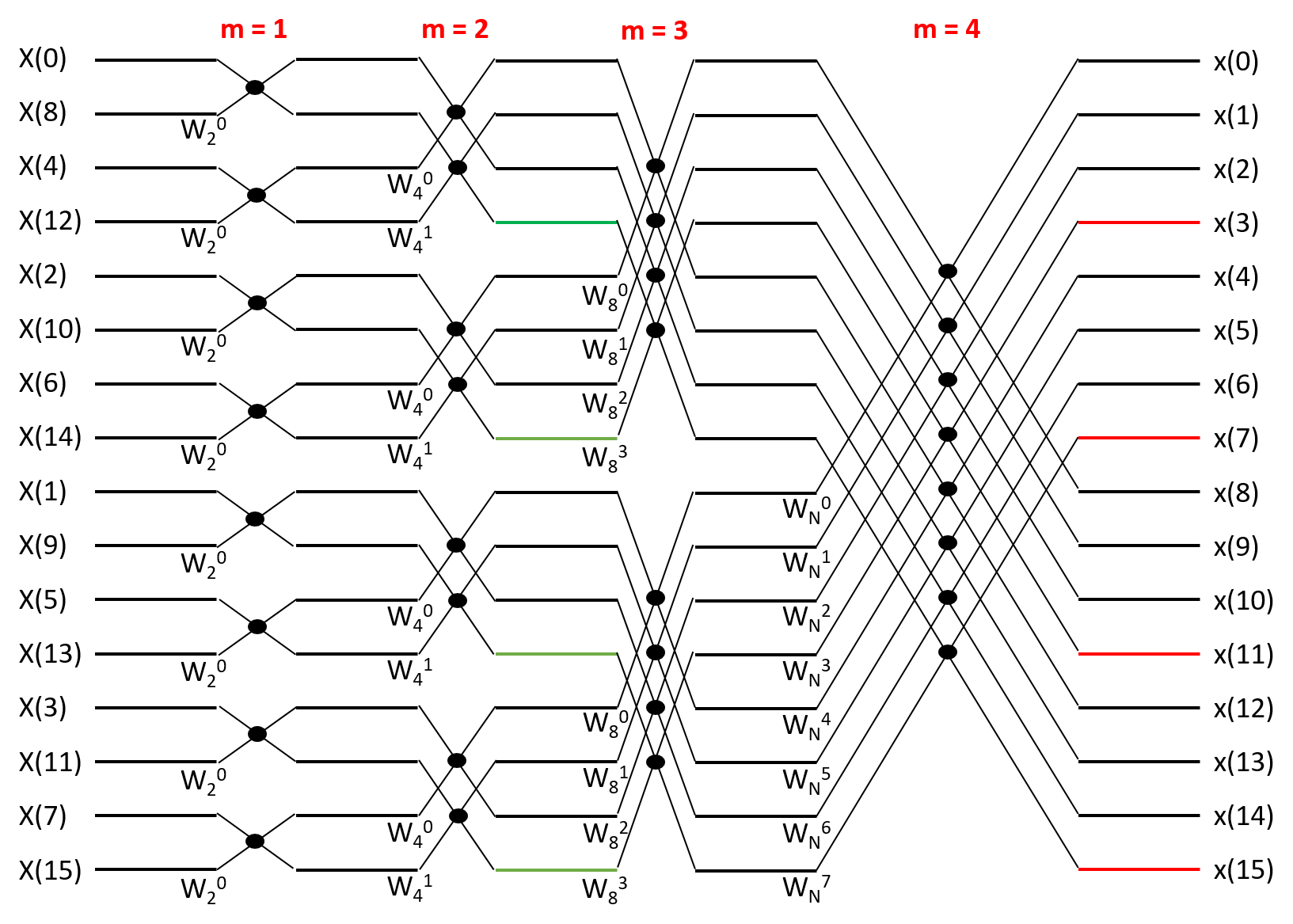
{//为节省CPU计算时间,旋转因子采用查表法处理// ★ 根据实际FFT的点数N_series,该表数据需自行修改// 以下结果通过Excel自动生成// WN[k].real = cos(2*PI/N*k);// WN[k].img = -sin(2*PI/N*k);} 【 16点 频域抽取法FFT(简称 DIF - FFT) 】
3.实现
这篇关于【C】快速傅里叶变换(FFT)讲解及实现的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!