傅里叶专题

【数字信号处理】一文讲清FFT(快速傅里叶变换)

目录快速傅里叶变换（Fast Fourier Transform，FFT）FFT的背景快速傅里叶变换（Fast Fourier Transform，FFT）DFT的数学表达实际计算重要性和应用频谱泄露、频谱混叠奈奎斯特采样定理参考链接快速傅里叶变换（Fast Fourier Transform，FFT） FFT的背景 1、为什么要时域→频域频率？50Hz+频率120Hz

傅里叶变换家族

禹晶、肖创柏、廖庆敏《数字图像处理（面向新工科的电工电子信息基础课程系列教材）》禹晶、肖创柏、廖庆敏《数字图像处理》资源二维码

【Get深一度】信号处理（二）——傅里叶变换与傅里叶级数的区别与联系

1.傅里叶级数和傅里叶变换：傅里叶级数对周期性现象做数学上的分析傅里叶变换可以看作傅里叶级数的极限形式，也可以看作是对周期现象进行数学上的分析。除此之外，傅里叶变换还是处理信号领域的一种很重要的算法。要想理解傅里叶变换算法的内涵，首先要了解傅里叶原理的内涵。傅里叶原理表明：对于任何连续测量的数字信号，都可以用不同频率的正弦波信号的无限叠加来表示。傅里叶变

【C】快速傅里叶变换（FFT）讲解及实现

引言基2FFT 1.引言人类的求知欲是永无止境的，自1965年 T. W. Cooley 和 J. W. Tuky 在《Math. Computation, Vol, 19, 1965》发表了著名的《 An algorithm for the machine calculation of complex Fourier series 》，人们对有关傅里叶变换的改进和创新就从未止步。1

线性代数|机器学习-P32循环矩阵的特征向量-傅里叶矩阵

文章目录 1. 大纲2. 循环矩阵2.1 移位矩阵P2.2 P的特征值和特征向量2.3 循环卷积矩阵2.4 循环卷积计算 3. 傅里叶矩阵 1. 大纲循环矩阵在机器学习，图像处理中的应用循环卷积矩阵的特征值，特征向量，卷积规则循环卷积矩阵多项式表达： C = c 0 I + c 1 P + c 2 P 2 + ⋯ + c n − 1 P n − 1 C=c_0 I+c_1P+c

NumPy（一）：简介【主要功能：操作数组、矩阵】【Python + NumPy == Matlab】【包括很多实用的数学函数】【覆盖了很多的数学领域，比如：线性代数、傅里叶变换、随机数生成】

一、NumPy是什么？ NumPy是一个开源的Python科学计算库。 Numerical Python 二、NumPy有什么功能 NumPy主要的功能之一用来操作数组和矩阵。 NumPy是科学计算、深度学习等高端领域的必备工具。使用TensorFlow、Caffe。框架训练神将网络模型时，需要进行大量复杂的计算，可以直接调用NumPy里面的API NumPy包含了很多实用的数学函数

短时傅里叶变换（Short-Time Fourier Transform, STFT），语音识别

高能预警！！！ .wav文件为笔者亲自一展歌喉录制的噪声，在家中播放，可驱赶耗子，蟑螂介绍短时傅里叶变换（Short-Time Fourier Transform, STFT）是一种时频分析方法，用于分析非平稳信号的频率成分随时间的变化。与传统的傅里叶变换不同，STFT在处理信号时考虑了时间局部性，使得它能够同时在时间域和频率域上分析信号。 STFT的背景傅里叶变换可以将信号从时间

MATLAB中的快速傅里叶变换FFT与IFFT

背景 FFT （Fast Fourier Transform）是离散傅立叶变换的快速算法，可以将一个信号从时域变换到频域。同时与之对应的是IFFT（Inverse Fast Fourier Transform）离散傅立叶反变换的快速算法。为掌握FFT和IFFT在MATLAB中的应用，我们需要了解FFT的基本原理。 MATLAB应用及原理 X = fft(x,N);x = ifft(X, N

C#实现快速傅里叶变换（FFT）

1、FFT类 using System;using System.Collections.Generic;using System.Linq;using System.Runtime.InteropServices.ComTypes;using System.Text;using System.Threading.Tasks;namespace DFT_FFTApp.Utils{pu

C# 实现傅里叶变化（DFT）

1、DFT函数类 using System;using System.Collections.Generic;using System.Linq;using System.Text;using System.Threading.Tasks;namespace DFT_FFTApp.Utils{public class DFT{/// <summary>/// DFT/// </summ

使用Python实现方波信号傅里叶变换

目录概述 1 方波信号 1.1 问题描述 1.2 傅里叶级数的数学实现 2 函数实现 2.1 方波信号实现 2.2 方波信号的傅里叶函数 3 测试函数 3.1 测试原理 3.2 改变K值的波形变化概述本文主要介绍使用使用Python实现方波信号傅里叶变换的方法，笔者首先介绍了方波信号的数学实现方法，还介绍了波形信号实现傅里叶变化的数学实现步骤，最后使用pyth

傅里叶分析分析好文章

转载文章——傅里叶分析之掐死教程（完整版）本文完全转载博主文章，未做修改，博客作者：韩昊谨以此文献给大连海事大学的吴楠老师，柳晓鸣老师，王新年老师以及张晶泊老师。转载的同学请保留上面这句话，谢谢。如果还能保留文章来源就更感激不尽了。要让读者在不看任何数学公式的情况下理解傅里叶分析。傅里叶分析不仅仅是一个数学工具，更是一种可以彻底颠覆一个人以前世界观

从头到尾彻底理解傅里叶变换算法、下

经典算法研究系列：十、从头到尾彻底理解傅里叶变换算法、下作者：July、dznlong 二零一一年二月二十二日推荐阅读：The Scientist and Engineer's Guide to Digital Signal Processing，By Steven W. Smith, Ph.D。此书地址：http://www.dspguide.com/pdfbook.htm。

数学--傅里叶分析-通俗易懂

作者：韩昊知乎：Heinrich 微博：@花生油工人知乎专栏：与时间无关的故事谨以此文献给大连海事大学的吴楠老师，柳晓鸣老师，王新年老师以及张晶泊老师。转载的同学请保留上面这句话，谢谢。如果还能保留文章来源就更感激不尽了。 ——更新于2014.6.6，想直接看更新的同学可以直接跳到第四章———— 我保证这篇文章和你以前看过的所有文章都不同，这是12年还在果壳的时

CV学习笔记6-一维傅里叶正、逆变换公式

傅里叶变换是一种重要的数学工具，用于将信号从时域转换到频域。傅里叶变换在信号处理、图像处理等领域有广泛的应用。以下是一维傅里叶变换的正变换和逆变换的公式： 1. 一维傅里叶正变换傅里叶正变换将时域信号转换为频域信号。其公式为： X ( f ) = ∫ − ∞ ∞ x ( t ) ⋅ e − j 2 π f t d t X(f) = \int_{-\infty}^{\infty} x(

快速傅里叶变换FFT的迭代实现

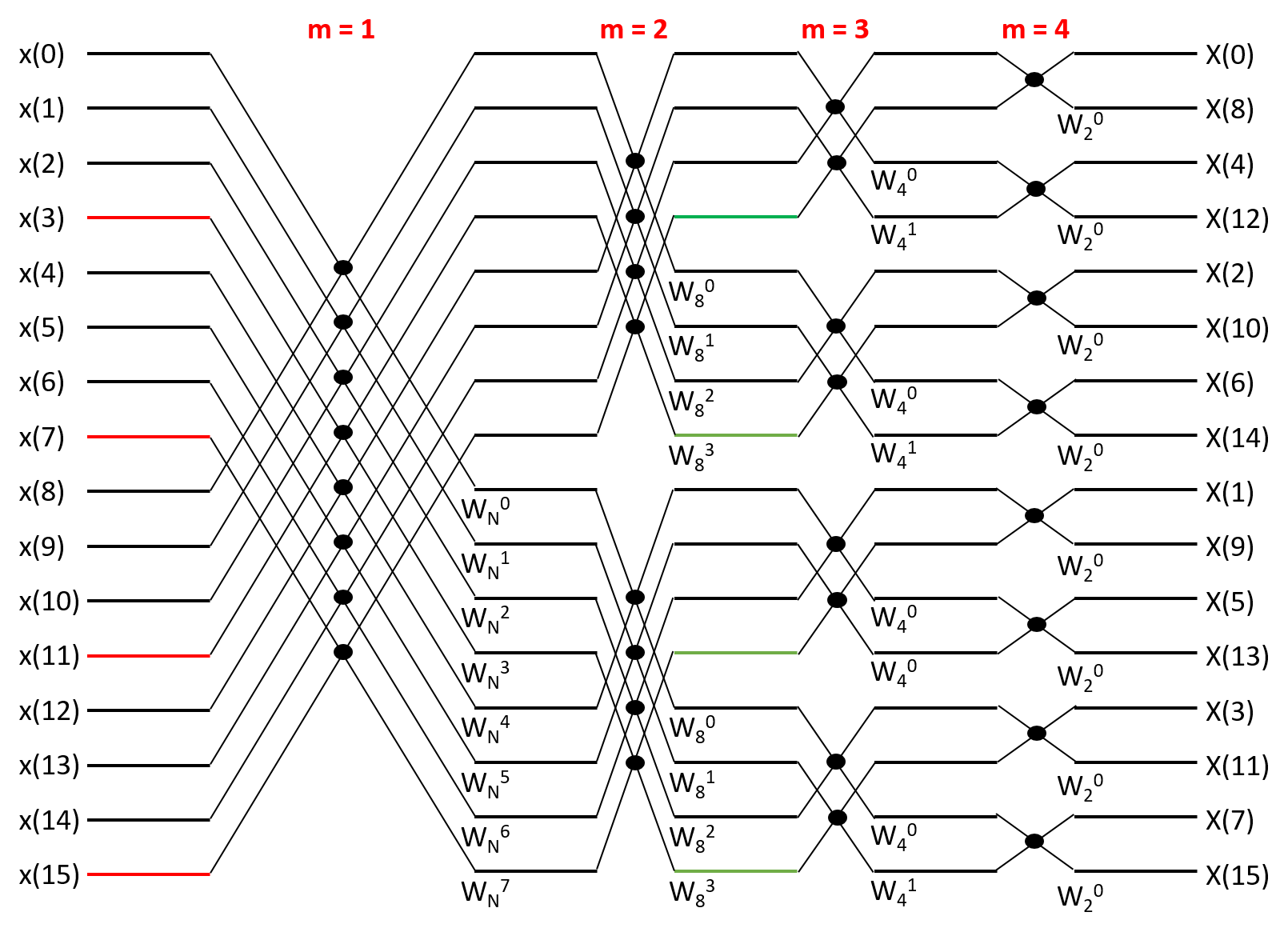
《快速傅里叶变换的相关定义、原理及其递归算法》描述了FFT的最基本原理，按2来分解原DFT运算。实际上有效率更高的分解办法（视卷积双方的长度而定），当然效率虽更高却更难以理解。即使按2来分解，也有基于时域的和基于频域的区别，上文描述的是基于时域的，个人觉得这是最容易理解的一种FFT原理。本文描述此原理下的FFT的迭代实现。仍然以8点DFT为例，考察其依次2分的过程，可以得到这样

快速傅里叶变换的相关定义、原理及其递归算法

快速傅里叶变换FFT是离散傅里叶变换DFT的一种快速算法，实际上诸如Matlab等科学计算软件都已经实现了FFT，只需调用相应的接口即可。在ACM里，FFT的典型应用就是大数的乘法或者多项式的乘法。顺便，如果题目规模不是很大，有关大数的运算推荐使用Java语言，使用java.math.BigInteger包完成；包括高精度运算，可以使用BigDecimal包完成。任何情况下，会一门外语总是

[转载]细说傅里叶变换

原文地址：[转载]细说傅里叶变换作者：小腹黑zju 原文出处：http://blog.163.com/niujiashu@126/blog/static/1002930422011102501211199/ 一、傅立叶变换的由来关于傅立叶变换，无论是书本还是在网上可以很容易找到关于傅立叶变换的描述，但是大都是些故弄玄虚的文章，太过抽象，尽是一些让人看了就望而生畏的公式的罗列

[信号与系统]傅里叶变换、卷积定理、和为什么时域的卷积等于频域相乘。

前言最近学习以下IIR滤波器和FIR滤波器前置 1. 时域和频域时域和频域代表着频率和时间与振幅的一一对应关系 2. 卷积运算关于卷积的定义，详情请看这篇文章能让你明白卷积卷积运算是一种数学运算，广泛应用于信号处理、图像处理、控制系统和概率论等领域。卷积运算可以看作是两个函数之间的一种积分操作，用于描述一个函数在另一个函数上的“滑动”效果。连续卷积：对于连续

【高等数学】傅里叶级数

最近刷了会抖音，看到一个非常有趣的现象：傅里叶级数，今天挑了几个视频来供大家学习。 1.傅里叶级数概念【小崔说数】傅里叶级数专题https://www.bilibili.com/video/BV1Uq4y1q7xk?t=117.4 2.傅里叶级数动画【谜之舒适】12分钟的傅立叶级数动画https://www.bilibili.com/video/BV1o4411D7vm?t=355.8

新旧torch中傅里叶变换实现（fft）

由泰勒级数我们知道，一个函数可以被分解成无穷个幂函数叠加的形式，于是同样地，一个周期函数也可以被分解成多个周期函数叠加，于是自然而然地，三角函数符合这个需求，由傅里叶级数我们可以将周期函数分解成无穷个三角函数叠加的形式，以下是具体的定义： # a, b 均为一个2维tensor# torch 1.8 之前（旧）def ccorr(a, b):aa = torch.rfft(a, 1)bb =

有趣的傅里叶变换与小波变换对比（Python）

不严谨的说，时域和频域分析就是在不同的空间看待问题的，不同空间所对应的原子(基函数)是不同的。你想一下时域空间的基函数是什么？频域空间的基函数是什么？一般的时-频联合域空间的基函数是什么？小波域空间的基函数是什么？有的空间域比较容易分析，有的空间域不容易分析。举个例子吧，首先加载一个双曲Chirp信号，数据的采样频率为2048Hz，第一个Chirp信号持续时间为0.1~0.68秒，第二个C

信号傅里叶变换后的实数和虚数部分理解

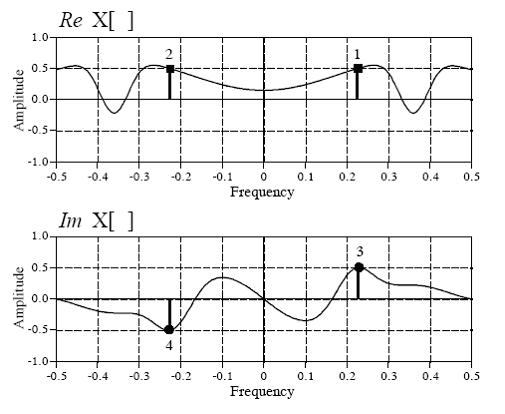
傅里叶（FFT、DFT、傅立叶、Fourier）傅里叶变换的结果为什么含有复数？为什么傅里叶变换的结果含有复数成份？看了很多关于FFT的资料，现在看到一个资料说FFT转换的结果是实部+虚部，所以不理解为什么从时域转到频域就会变成复数。第一，从定义式上看，积分号里含有复数，积分结果是复数；第二，从傅立叶变换的物理意义上看：FT变换是将一个信号分解为多个信号之和的形式，并且是正弦或余弦信号

傅里叶变换科普知识

学习傅里叶变换需要面对大量的数学公式，数学功底较差的同学听到傅里叶变换就头疼。事实上，许多数学功底好的数字信号处理专业的同学也不一定理解傅里叶变换的真实含义，不能做到学以致用!事实上，傅里叶变换的相关运算已经非常成熟，有现成函数可以调用。对于绝大部分只需用好傅里叶变换的同学，重要的不是去记那些枯燥的公式，而是解傅里叶变换的含义及意义。本文试图不用一个数学公式，采用较为通俗的语言深入

27、matlab傅里叶变换：fft()函数

1、fft 快速傅里叶变换语法 Y = fft(X) 使用快速傅里叶变换 (FFT) 算法计算 X 的离散傅里叶变换 (DFT)。 Y = fft(X,n) 返回 n 点 DFT。 Y = fft(X,n,dim) 返回沿维度 dim 的傅里叶变换。例如，如果 X 是矩阵，则 fft(X,n,2) 返回每行的 n 点傅里叶变换含噪信号 1）原始信号加噪声代码 Fs = 1000;

【信号加密】基于傅里叶变换和小波变换对音频水印的嵌入、提取matlab代码

% 读取原始音频文件 audio = audioread(‘original_audio.wav’); % 读取水印图像 watermark = imread(‘watermark_image.png’); % 将水印图像转换为灰度图像 watermark_gray = rgb2gray(watermark); % 调整水印图像尺寸以适应音频 watermark_resized = imre