[信号与系统]傅里叶变换、卷积定理、和为什么时域的卷积等于频域相乘。

本文主要是介绍[信号与系统]傅里叶变换、卷积定理、和为什么时域的卷积等于频域相乘。，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

前言

最近学习以下IIR滤波器和FIR滤波器

前置

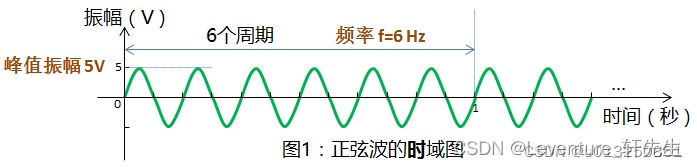
1. 时域和频域

时域和频域代表着频率和时间与振幅的一一对应关系

2. 卷积运算

关于卷积的定义，详情请看 这篇文章能让你明白卷积

卷积运算是一种数学运算，广泛应用于信号处理、图像处理、控制系统和概率论等领域。卷积运算可以看作是两个函数之间的一种积分操作，用于描述一个函数在另一个函数上的“滑动”效果。

连续卷积：

对于连续函数$f(t)$和$g(t)$它们的卷积定义为：

$$(f\ast g)(t)={\int }_{-\infty }^{\infty }f(\tau )g(t-\tau )d\tau$$

离散卷积

对于离散函数 $f[n]$ 和 $g[n]$，他们的卷积定义为：

$$(f\ast g)[n]=\sum _{k=-\infty }^{\infty }f[k]g[n-k]$$

卷积运算的性质

1. 交换律
$$f\ast g=g\ast f$$
这意味着两个函数的卷积不受顺序影响。

2. 结合律（结合性）
$$(f\ast g)\ast h=f\ast (g\ast h)$$
这意味着多重卷积的计算顺序可以随意改变。

3.分配律
$$f\ast (g+h)=(f\ast g)+(f\ast h)$$

这意味着卷积运算对加法是分配的。

4. 与冲激函数的卷积（单位冲激函数）

对于单位冲激函数$\delta (t)$有：

$$f\ast \delta =f$$
这意味着任何函数与单位冲激函数的卷积等于该函数本身。

5.平移性

$$f(t-t_0)\ast g(t)=(f\ast g)(t-t_0)$$
这意味着函数的平移在卷积后仍然保留。

卷积定理

在傅里叶变换域中，卷积运算可以转化为点乘运算。具体来说，如果$F(\omega )$ 和 $G(\omega )$分别是 $f(t)$ 和 $g(t)$ 的傅里叶变换，那么：

F { f ∗ g } = F { f } ⋅ F { g } \mathcal{F}\{f * g\} = \mathcal{F}\{f\} \cdot \mathcal{F}\{g\} F{f∗g}=F{f}⋅F{g}

反之亦然，即傅里叶变换的点乘可以通过逆傅里叶变换转化为时域的卷积运算。

3. 傅里叶变换

傅里叶变换将一个时域信号转换到频域，使得可以分析信号的频率成分。对于非周期信号，傅里叶变换定义为：

$F(w)={\int }_{-\infty }^{\infty }f(t)e^{-j\pi t}dt$

其中$F(w)$是频域表示，称为频谱。$f(t)$是时域信号,w是角频率

逆傅里叶变换可以将频域信号转换回时域：

$f(t)=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }F(w)e^{j\pi t}dw$

关键点包括：

1. 频域与时域的对应关系：时域信号可以通过傅里叶变换转换到频域，反之亦然。这提供了分析和处理信号的新方法。

2. 频谱：傅里叶变换的结果$F(w)$称为信号的频谱，表示信号在不同频率成分上的分布。

3. 正交性 ： 正弦和余弦函数是正交的，这使得傅里叶级数能够分解任何周期信号，而傅里叶变换能够分解任何非周期信号。

4. 卷积定理 ： 时域中的卷积对应于频域中的乘积，这大大简化了信号处理中的卷积运算。

我们常见的其实会由这个卷积定理延申出来一个定理：

为了接下来的这个问题，我们需要用到一些傅里叶变换的性质：

1. 线性性质

傅里叶变换是线性的。对于任意两个信号 $x_1(t)$ 和 $x_2(t)$，以及任意常数 $a$ 和 $b$，有：

F { a x 1 ( t ) + b x 2 ( t ) } = a X 1 ( ω ) + b X 2 ( ω ) \mathcal{F}\{a x_1(t) + b x_2(t)\} = a X_1(\omega) + b X_2(\omega) F{ax1​(t)+bx2​(t)}=aX1​(ω)+bX2​(ω)

2. 平移性质

如果一个信号 $x(t)$ 在时域上平移 $t_0$，其傅里叶变换为：

F { x ( t − t 0 ) } = X ( ω ) e − i ω t 0 \mathcal{F}\{x(t - t_0)\} = X(\omega) e^{-i\omega t_0} F{x(t−t0​)}=X(ω)e−iωt0​

3. 调制性质

如果一个信号 $x(t)$ 在时域上乘以一个复指数函数 $e^{i{\omega }_{0}t}$，其傅里叶变换为：

F { x ( t ) e i ω 0 t } = X ( ω − ω 0 ) \mathcal{F}\{x(t) e^{i\omega_0 t}\} = X(\omega - \omega_0) F{x(t)eiω0​t}=X(ω−ω0​)

4. 微分性质

如果一个信号 $x(t)$ 的导数 $\frac{d^{n}x(t)}{d{t}^n}$ 存在，其傅里叶变换为：

$$\mathcal{F}\left\{\frac{d^{n}x(t)}{d{t}^n}\right\}=(i\omega {)}^{n}X(\omega )$$

5. 卷积性质
如果两个信号 $x_1(t)$ 和 $x_2(t)$ 的卷积 $(x_1\ast x_2)(t)$ 存在，其傅里叶变换为：

$$\mathcal{F}\{(x_1\ast x_2)(t)\}=X_1(\omega )\cdot X_2(\omega )$$

时域的卷积等于频域相乘

这是怎么来的呢，我们首先知道两个时域信号$x(t)$和$h(t)$的卷积：

$$(x\ast h)(t)={\int }_{-\infty }^{\infty }x(\tau )h(t-\tau )d\tau$$

我们得到X(f)和H(f)是他们分别通过傅里叶变换得到的频域表示，那么时域中的卷积$x(t)\ast h(t)$就对应于频域中的乘积 $X(f)\cdot H(f)$
也就是说，时域中的复杂操作，我们最后用频域中的简单操作就可以指代了。

换句话说：

时域信号可以分解成一串不同频率正弦信号的叠加。根据卷积的分配率，两个时域信号的卷积最终可以展开成两两正弦信号的卷积的和。由于不同频率的正弦信号的卷积为0，所以最终只剩下相同频率的正弦信号的卷积。而卷积的结果就是频率不变，幅度相乘。
在频域里边就表现为直接相乘。

关于这句话，我们还可以生硬的推导一下：

推导

卷积定理的推导

我们首先知道两个时域信号 $x(t)$ 和 $h(t)$ 的卷积定义为：

$$(x\ast h)(t)={\int }_{-\infty }^{\infty }x(\tau )h(t-\tau )d\tau$$

令 $y(t)=(x\ast h)(t)$，则 $y(t)$ 是 $x(t)$ 和 $h(t)$ 的卷积。

傅里叶变换

对 $y(t)$ 进行傅里叶变换：

Y ( f ) = F { y ( t ) } = F { ∫ − ∞ ∞ x ( τ ) h ( t − τ ) d τ } Y(f) = \mathcal{F}\{y(t)\} = \mathcal{F}\left\{\int_{-\infty}^{\infty} x(\tau) h(t - \tau) \, d\tau\right\} Y(f)=F{y(t)}=F{∫−∞∞​x(τ)h(t−τ)dτ}

根据傅里叶变换的线性性质，我们可以将积分符号放到傅里叶变换操作符的前面：

Y ( f ) = ∫ − ∞ ∞ x ( τ ) F { h ( t − τ ) } d τ Y(f) = \int_{-\infty}^{\infty} x(\tau) \mathcal{F}\{h(t - \tau)\} \, d\tau Y(f)=∫−∞∞​x(τ)F{h(t−τ)}dτ

时移性质

根据傅里叶变换的时移性质，如果 $h(t-\tau )$ 的傅里叶变换为 $H(f)$，则：

F { h ( t − τ ) } = H ( f ) e − i 2 π f τ \mathcal{F}\{h(t - \tau)\} = H(f) e^{-i2\pi f \tau} F{h(t−τ)}=H(f)e−i2πfτ

将其代入上式：

$$Y(f)={\int }_{-\infty }^{\infty }x(\tau )H(f)e^{-i2\pi f\tau }d\tau$$

分离变量

将 $H(f)$ 从积分符号中分离出来：

$$Y(f)=H(f){\int }_{-\infty }^{\infty }x(\tau )e^{-i2\pi f\tau }d\tau$$

这里， ${\int }_{-\infty }^{\infty }x(\tau )e^{-i2\pi f\tau }d\tau$ 是 $x(t)$ 的傅里叶变换：

$$X(f)={\int }_{-\infty }^{\infty }x(\tau )e^{-i2\pi f\tau }d\tau$$

因此：

$$Y(f)=X(f)\cdot H(f)$$

总结

我们得到了频域中的乘积：

$$Y(f)=X(f)\cdot H(f)$$

这表明时域中的卷积对应于频域中的乘积。这就是卷积定理的内容。

这篇关于[信号与系统]傅里叶变换、卷积定理、和为什么时域的卷积等于频域相乘。的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---