fft专题
【数字信号处理】一文讲清FFT(快速傅里叶变换)
目录 快速傅里叶变换（Fast Fourier Transform，FFT）FFT的背景快速傅里叶变换（Fast Fourier Transform，FFT）DFT的数学表达实际计算重要性和应用频谱泄露、频谱混叠奈奎斯特采样定理参考链接 快速傅里叶变换（Fast Fourier Transform，FFT） FFT的背景 1、为什么要时域→频域频率？50Hz+频率120Hz
【BNU】40719 Arithmetic Progressions【分块+FFT】
传送门：【BNU】40719 Arithmetic Progressions 题目分析： 用分块+FFT强行AC了这题…… 之前一直TLE……然后改了好久把姿势改的优美点了……终于过了…… 大概思路是：我们考虑分块，假设每一块的大小为S，一共分了B块然后我们分两种情况讨论： 1.第二个数在第i块，第一个数在(1~i-1)块内，第三个数在(i+1~B)块内。 2.至少两个数在同一块内。
【HDU】5197 DZY Loves Orzing 【FFT启发式合并】
传送门：【HDU】5197 DZY Loves Orzing 题目分析： 首先申明，我不会 dp dp方程= =……这个东西给队友找出来了，然后我就是套这个方程做题的Qrz…… 对于这题，因为 n2 n^2个数互不相同，所以每一列都可以单独考虑。设 dpni dp_ni表示长度为 n n的排列，能恰好看见ii个人的方案数，根据队友的发现， dpni dp_ni就等于 |sni| |s_ni|
【ZOJ】3874 Permutation Graph 【FFT+CDQ分治】
传送门：【ZOJ】3874 Permutation Graph 题目分析： 容易知道一个个连通块内部的标号都是连续的，否则一定会有另一个连通块向这个连通块建边，或者这个连通块向另一个连通块建边。而且从左到右左边的连通块内最大的标号小于右边连通块内最小的标号。 然后我们可以构造dp方程： dp[n]=n!−i!∗dp[n−i] \qquad \qquad dp[n] = n! - i! *
【SPOJ】Triple Sums【FFT】
传送门：【SPOJ】Triple Sums 题目分析： 首先我们不考虑 i<j<k i<j<k这个条件，构造多项式： Y=∑xai \qquad\qquad\qquad Y = \sum x^{a_i} 那么 ai+aj+ak=S ai+aj+ak=S的个数即 xai+aj+ak=S x^{a_i+a_j+a_k=S}的个数，等价于 Y3中xS Y^3中x^S的系数。 然后我们考虑容斥
【BNU】33943 Super Rooks on Chessboard 【FFT】
【BNU】33943 Super Rooks on Chessboard UVA上的题，然而我怎么会蠢到去UVA呢！（其实是百度首先跳出来的是BNU → \to_ → \to） 题目分析： 设 numx numx为 N N个车没有覆盖的行数，numynumy为 N N个车没有覆盖的列数。 首先我们考虑没有主对角线覆盖这一条件时，总共的没有被覆盖的面积就是numx∗numynumx \ast
【HDU】4609 3-idiots 【FFT】
传送门：【HDU】4609 3-idiots 题目分析： 我们考虑两边长度之和为 n n的方案数，设num[x]num[x]为长度为 x x的个数，那么∑nx=1num[n−x]∗num[x]\sum_{x=1}^{n}{num[n-x]*num[x]} 即两边长度之和为 n n的方案数。容易发现这这正是卷积！然后我们就可以愉快的用FFTFFT预处理出所有的两边长度之和为i的方案数。 FFT
【codechef】 Prime Distance On Tree【求树上路经长度为i的路径条数】【点分治+FFT】
传送门：【codechef】 Prime Distance On Tree 点分治+FFT水题……竟然n*n爆int没发现…… 而且NTT TLE，FFT跑的超级快…… my code: my~~code: #include <bits/stdc++.h>using namespace std ;typedef long long LL ;#define clr( a , x ) m
【51nod】算法马拉松4 F 移数字 【快速求N!%P】【FFT】
传送门：【51nod】算法马拉松4 F 移数字 涉及知识点：多项式求逆，多项式除法，多点插值，阶乘取模。 对于N!%P，复杂度为 O(N−−√log2N−−√) O(\sqrt N \log^2\sqrt N)。 但常数巨大，和暴力算实际复杂度只相差常数= = 这个是可以扩展到组合数取模的~ my code: my~~code: #include <stdio.h>#includ
【HDU】5958 New Signal Decomposition【离散对数下的FFT】
题目链接：【HDU】5958 New Signal Decomposition 在此先感谢小q对我的指导，没有q老师的帮助，估计永远也做不出来了。 首先我们考虑对这个式子做离散对数。令 g g为pp的某个原根，则有： bi=∑p−1j=0aj⋅r(i,j) \quad b_i=\sum_{j=0}^{p-1}a_j\cdot r(i,j) bi=∑p−1j=0aj⋅2sin32πi⋅j
【C】快速傅里叶变换（FFT）讲解及实现
引言基2FFT 1.引言 人类的求知欲是永无止境的，自1965年 T. W. Cooley 和 J. W. Tuky 在《Math. Computation, Vol, 19, 1965》发表了著名的《 An algorithm for the machine calculation of complex Fourier series 》，人们对 有关傅里叶变换的改进和创新就从未止步。1
短时相关+FFT捕获方法的MATLAB仿真
提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档 短时相关+FFT捕获方法的MATLAB仿真 前言短时相关+FFT捕获相关原理1、频偏引起的相关损失2、扇贝损失 MATLAB程序获取完整程序 前言 对于算法类的工程，FPGA设计，仿真先行，再没搞清楚整个信号处理原理和流程之前，切莫盲目开始FPGA RTL。对于导航接收机而言，接收机的第一步就在于能够捕
Xilinx FFT IP使用
简介 本章节主要介绍FFT原理，以及Xilinx的FFT IP使用说明做详细介绍。 FFT介绍 FFT主要是将时域信号转换成频域信号，转换后的信号更方便分析。首先，FFT是离散傅立叶变换 (DFT) 的快速算法，那么说到FFT，我们自然要先讲清楚傅立叶变换。先来看看傅立叶变换是从哪里来的？ 傅立叶原理表明：任何连续测量的时序或信号，都可以表示
MATLAB中的快速傅里叶变换FFT与IFFT
背景 FFT （Fast Fourier Transform）是离散傅立叶变换的快速算法，可以将一个信号从时域变换到频域。同时与之对应的是IFFT（Inverse Fast Fourier Transform）离散傅立叶反变换的快速算法。为掌握FFT和IFFT在MATLAB中的应用，我们需要了解FFT的基本原理。 MATLAB应用及原理 X = fft(x,N);x = ifft(X, N
Hdu 1 402 FFT 大整数相乘 Hoj10005
传送门：http://acm.hdu.edu.cn/showproblem.php?pid=1402 A * B Problem Plus Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others) Total Submission(s): 14721 Accepted Sub
Hdu 4609 FFT
传送门：http://acm.hdu.edu.cn/showproblem.php?pid=4609 3-idiots Time Limit: 10000/5000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Submission(s): 2918 Accepted Submission(s
C#实现快速傅里叶变换（FFT）
1、FFT类 using System;using System.Collections.Generic;using System.Linq;using System.Runtime.InteropServices.ComTypes;using System.Text;using System.Threading.Tasks;namespace DFT_FFTApp.Utils{pu
非整周期截取信号对FFT分析的影响
原文出自微信公众号【小小的电子之路】 自然界中的模拟信号大部分都是无限长的，或者说对计算机而言可以说是无限长的，而计算机只能处理有限长的信号，怎么办呢？以快速傅里叶变换为例，我们通常是截取目标信号中有限长的一小段数据进行分析，那么问题来了，FFT在分析的时候是怎么通过那一小段输入数据来推断原始目标信号波形的呢？ 以正弦信号为例，该信号是一个无限长的模拟信号，我们在FFT分析的时候只会截取
Matlab FFT参数设置研究
写在前面的废话 近期要对一款高速ADC进行测试，用到Matlab的fft函数分析其动态性能，为了对Matlab 的fft有一个全方位立体的认识，对其参数进行了小实验，记录如下。 使用Matlab生成采样数据 clear;fs = 1000;ts = 1/fs;L = 2400;t = (0:L-1)*ts;x = 0.7*sin(2*pi*50*t) + sin(2*pi*120
【HDU】1402 A * B Problem Plus 【FFT】
传送门：【HDU】1402 A * B Problem Plus 题目分析： 这就是大数乘法题，问两个大数相乘的结果，由于O(n2)的算法复杂度太大，所以我们用FFT来优化他。关于FFT网上资料很多，我就不多说啦。 这是我做的第一道FFT，FFT是看算法导论学来的，前面几篇文章是从july大神那边转载来的，感觉都讲的很不错，简单易懂~ // whn6325689//
【正点原子K210连载】第三十二章 音频FFT实验 摘自【正点原子】DNK210使用指南-CanMV版指南
第三十二章 音频FFT实验 本章将介绍CanMV下FFT的应用，通过将时域采集到的音频数据通过FFT为频域。通过本章的学习，读者将学习到CanMV下控制FFT加速器进行FFT的使用。 本章分为如下几个小节： 32.1 maix.FFT模块介绍 32.2 硬件设计 32.3 程序设计 32.4 运行验证 32.1 maix.FFT模块介绍 Kendryte K210片上拥有一个FFT Accel
![[vivado][IP核]FFT](https://img-blog.csdn.net/20180705090837930?watermark/2/text/aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3UwMTIxMzUwNzA=/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70)
FFT的迭代程序实现——hdu1402
《快速傅里叶变换FFT的迭代实现》描述了最简单的FFT的迭代实现，在此基础上可以用它进行大整数乘法或者多项式乘法。不过，还需要考虑IDFT的快速实现。IDFT有2种实现方式。第一种仿照FFT，观察IDFT的定义式，和DFT的定义本质上没有区别，利用单位复根的性质可以写出IFFT。第二种方法则利用共轭的性质： 即：逆变换等于共轭的变换的共轭，所以可以复用FFT的实现代码。
快速傅里叶变换FFT的迭代实现
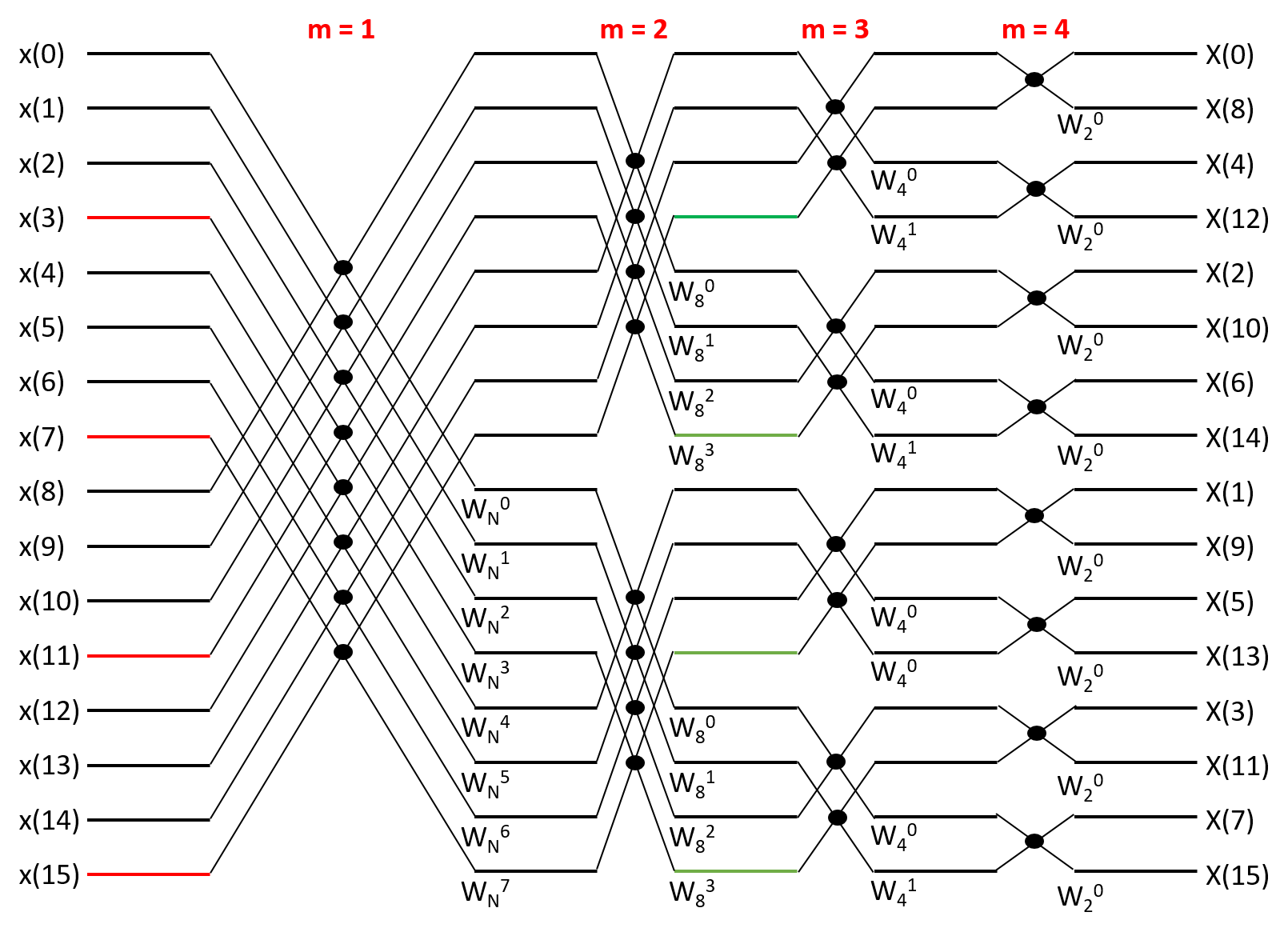
《快速傅里叶变换的相关定义、原理及其递归算法》描述了FFT的最基本原理，按2来分解原DFT运算。实际上有效率更高的分解办法（视卷积双方的长度而定），当然效率虽更高却更难以理解。即使按2来分解，也有基于时域的和基于频域的区别，上文描述的是基于时域的，个人觉得这是最容易理解的一种FFT原理。本文描述此原理下的FFT的迭代实现。 仍然以8点DFT为例，考察其依次2分的过程，可以得到这样
新旧torch中傅里叶变换实现（fft）
由泰勒级数我们知道，一个函数可以被分解成无穷个幂函数叠加的形式，于是同样地，一个周期函数也可以被分解成多个周期函数叠加，于是自然而然地，三角函数符合这个需求，由傅里叶级数我们可以将周期函数分解成无穷个三角函数叠加的形式，以下是具体的定义： # a, b 均为一个2维tensor# torch 1.8 之前（旧）def ccorr(a, b):aa = torch.rfft(a, 1)bb =
快速傅立叶变换（FFT）C语言函数
/*********************************************************************快速福利叶变换C函数函数简介：此函数是通用的快速傅里叶变换C语言函数，移植性强，以下部分不依赖硬件。此函数采用联合体的形式表示一个复数，输入为自然顺序的复数（输入实数是可令复数虚部为0），输出为经过FFT变换的自然顺序的复数使用说明：使用此函数只需更改宏定义F