微分方程专题
深度学习中的可微编程:从微分方程到物理模拟
引言 可微编程(Differentiable Programming)是深度学习领域的一个新兴概念,旨在将传统编程中的数学模型(如微分方程)与深度学习模型结合,构建出更加灵活、可解释的模型。这一技术为物理模拟、科学计算等领域带来了新的可能性,使得深度学习不仅能够进行预测,还能融入复杂的物理规律进行精确模拟。本篇博文将探讨可微编程的基本原理、常见应用场景,特别是在物理模拟中的实践,以及未来的发展方
一阶微分方程的解的存在唯一性定理
本篇笔记的内容来源 常微分方程(第四版) (王高雄,周之铭,朱思铭,王寿松) 高等教育出版社 利普希茨(Lipschitz)条件 考虑导数已解出的一阶微分方程 d y d x = f ( x , y ) (1) \frac{\mathrm{d}y}{\mathrm{d}x}=f(x,y)\tag{1} dxdy=f(x,y)(1) 其中 f ( x , y ) f(x,y) f(
微分方程_by小崔说数
可降解的微分方程 不显含x:y两撇=dp/dx=dp/dy*dy/dx 不显含y:dp/dx 都是y撇等于p 自变量与因变量呼唤 讲解为一阶线性微风方程 ,变成可分离得 公式得 高阶可降解得微分方程 通解=非齐
东南大学研究生-数值分析上机题(2023)Python 6 常微分方程数值解法
常微分方程初值问题数值解 6.1 题目 编制RK4方法的通用程序;编制AB4方法的通用程序(由RK4提供初值);编制AB4-AM4预测校正方法通用程序(由RK4提供初值);编制带改进的AB4-AM4预测校正方法通用程序(由RK4提供初值);对于初值问题 { y ′ = − x 2 y 2 , 0 ≤ x ≤ 1.5 , y ( 0 ) = 3 \begin{cases} y'=-x^{2}y
地震微分方程代码 - 第一部分
Seismic stencil codes - part 1 — ROCm Blogs (amd.com) 2024年8月12日,作者:[Justin Chang](Justin Chang — ROCm Blogs) 和 [Ossian O’Reilly](Ossian O’Reilly — ROCm Blogs)。 在高性能计算(HPC)领域,地震工作负载一直以来都依赖于结构网格上的高
微分方程(Blanchard Differential Equations 4th)中文版Section6.3
二阶线性方程 Laplace 变换求解 在这一节中,我们将拉普拉斯变换方法扩展到二阶常系数强迫线性方程,即具有以下形式的方程: d 2 y d t 2 + p d y d t + q y = f ( t ) , \frac{d^2 y}{dt^2} + p \frac{dy}{dt} + qy = f(t), dt2d2y+pdtdy+qy=f(t), 其中 p p p 和 q q
微分方程(Blanchard Differential Equations 4th)中文版Section5.1
平衡点分析 从第3章的工作中,我们能够对线性系统的解有定性和解析的理解。不幸的是,非线性系统通常不容易使用我们开发的解析和代数技术来分析,但我们可以利用线性系统的数学来理解非线性系统在其平衡点附近的行为。 Van der Pol 方程 为了说明如何分析平衡点附近解的行为,我们从一个简单但重要的非线性系统——Van der Pol 系统开始。回顾一下,Van der Pol 系统是: d x
微分方程(Blanchard Differential Equations 4th)中文版Section4.4
稳态的振幅和相位系统 在本节中,我们回到方程 d 2 y d t 2 + p d y d t + q y = cos ω t \frac{d^2 y}{dt^2} + p \frac{dy}{dt} + qy = \cos \omega t dt2d2y+pdtdy+qy=cosωt 用于周期性强迫的阻尼谐振子。我们的目标是建立解决方案行为与参数之间的定量关系——特别是决定强迫频率
微分方程(Blanchard Differential Equations 4th)中文版Section3.5
特殊情况: 重根和零特征值的线性系统 在前面的三节中,我们讨论了线性系统 d Y d t = A Y \frac{dY}{dt} = AY dtdY=AY 其中 2 × 2 2 \times 2 2×2 矩阵 A A A 具有两个不同的非零实特征值或一对复共轭特征值。在这些情况下,我们能够使用特征值和特征向量来草绘 x y xy xy 相平面的解,绘制 x ( t ) x(t)
【自动驾驶】控制算法(四)坐标变换与横向误差微分方程
写在前面: 🌟 欢迎光临 清流君 的博客小天地,这里是我分享技术与心得的温馨角落。📝 个人主页:清流君_CSDN博客,期待与您一同探索 移动机器人 领域的无限可能。 🔍 本文系 清流君 原创之作,荣幸在CSDN首发🐒 若您觉得内容有价值,还请评论告知一声,以便更多人受益。 转载请注明出处,尊重原创,从我做起。 👍 点赞、评论、收藏,三连走一波,让我们一起养成好习惯😜 在这里,您将
利用Matlab求解常微分方程(dsolve与ode45)
1.微分方程的基本概念 含义微分方程(英语:Differential equation,DE)是一种数学方程,用来描述某一类函数与其导数之间的关系。微分方程的通解是一个符合方程的函数。而在初等数学的代数方程里,解析解是一个具体的值。 (维基百科)一般的凡是表示未知函数、未知函数的导数与自变量之间的关系的方程,叫做微分方程。未知函数是一元函数的,叫常微分方程(ODE);未知函数是多元函数的叫做偏微
微分方程(Blanchard Differential Equations 4th)中文版Section2.3
阻尼谐振子 在本节中,我们将描述一种解析技术,它适用于本书中最重要的模型之一——阻尼谐振子。这一二阶微分方程用于建模各种现象,如质量-弹簧系统、电路理论中的RLC电路,以及人体的血糖调节系统。 例如,考虑汽车的悬挂系统。它可以平滑崎岖道路上的颠簸,并帮助保持轮胎与地面的接触。我们主要关注悬挂中的弹簧和减震器(见图2.34和2.35)。弹簧吸收由路面颠簸引起的力,并保持轮胎与道路接触。减震器由一
PINN解偏微分方程实例4
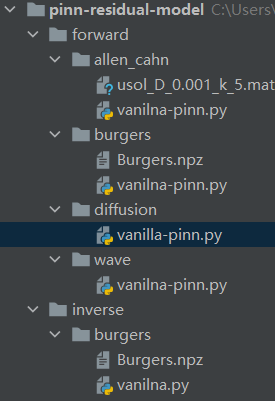
PINN解偏微分方程实例4 一、正问题1. Diffusion equation2. Burgers’ equation3. Allen–Cahn equation4. Wave equation 二、反问题1. Burgers’ equation3. 部分代码示例 本文使用 PINN解偏微分方程实例1中展示的代码求解了以四个具体的偏微分方程,包括Diffusion,Burg
Python重力弹弓流体晃动微分方程模型和交直流电阻电容电路
🎯要点 🎯计算地球大气层中热层金属坠物运动轨迹 | 🎯计算炮弹最佳弹射角度耦合微分方程 | 🎯计算电磁拉莫尔半径螺旋运动 | 🎯计算航天器重力弹弓运动力学微分方程 | 🎯计算双摆的混沌运动非线性微分方程,绘制相空图 | 🎯计算绝热和无粘流流体力学微分方程 | 🎯计算容器流体晃动自由表面简谐运动数学模型 | 🎯计算化学物质的伦纳德-琼斯势物理模型 | 🎯分析直流交流电阻电容电路
【matlab】微分方程建模基础讲解
tips: 需要有高等数学知识基础 1.求微分方程的解析解 matlab命令: dsolve(‘方程1’, ‘方程2’,…‘方程n’, ‘初始条件’, ‘自变量’) 例如:d²y/dx²=0,对应表达式为D2y=0。 exm:求通解 dsolve('Du=1+u^2','t') exm:方程组情况 [x,y,z]=dsolve('Dx=2*x-3*y+3*z','Dy=4*x-
基于Itô扩散过程的交易策略偏微分方程matlab求解与仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.本算法原理 5.完整程序 1.程序功能描述 基于Itô扩散过程的交易策略偏微分方程,提出了一种确定Itô扩散过程。通过根据的第一次通过时间来确定问题在这个过程中,我们推导出交易长度的分布函数和密度函数,并使用它们函数来计算策略的预期交易频率。 2.测试软件版本以及运行结果展示 MAT
为什么用SDE(随机微分方程)来描述扩散过程【论文精读】
为什么用SDE(随机微分方程)来描述扩散过程【论文精读】 B站视频:为什么用SDE(随机微分方程)来描述扩散过程 论文:Score-Based Generative Modeling through Stochastic Differential Equations 地址:https://doi.org/10.48550/arXiv.2011.13456 视频讲解内容目录 扩散过程就
Python俄罗斯方块可操纵卷积分类 | 稀疏辨识算法 | 微分方程神经求解器
🎯要点 🎯组卷积网络:实现循环组,可视化组动作,实现提升卷积核,MNIST 训练数据集训练组卷积网络的泛化能力 | 🎯可操控卷积网络:紧群的表征与调和分析,代码验证常规表征结果,不可约表征实现,傅里叶变换对群调和分析,实现可操控卷积网络 | 🎯深度概率模型:给定高维和结构化对单变量响应变量建模,实现分类响应模型,顺序响应模型、序列标记模型 | 🎯深度离散潜变量模型:使用FashionM
常微分方程 (ODE) 和 随机微分方程 (SDE)
常微分方程(Ordinary Differential Equations, ODE)和随机微分方程(Stochastic Differential Equations, SDE)是数学中描述系统动态行为的重要工具。它们有一些相似之处,但在处理随机性方面存在显著差异。 常微分方程 (ODE) 常微分方程描述的是确定性系统的动态行为,其中系统的状态随时间演变而变化。ODE的一般形式为: d
求解常微分方程初值问题之多步Euler预报-校正法
//实现多步Euler法 #include <iostream> #include <math.h> #include <iomanip> using namespace std; class multi_euler { private: int i, n; double f, h, x, x_last, yc, yc_old, yp; public: double func(doub
求解常微分方程初值问题之多变量Runge_Kutta_Gill法
//用RKG法求解常微分方程组 #include <iostream> #include <math.h> #include <iomanip> #include <fstream> using namespace std; class s_ode { private: int i, j, l, n; double a, b, c, d, h, x, x1, xi, xf; double
求解常微分方程初值问题之Runge_Kutta_Fehlberg法
//用Runge_Kutta_Fehlberg法求解微分方程 #include <iostream> #include <math.h> #include <iomanip> #include <fstream> using namespace std; class rkf { private: int flag; double eps, error, f, h, hnew, x, xf,