本文主要是介绍【matlab】微分方程建模基础讲解,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
tips:
需要有高等数学知识基础
1.求微分方程的解析解
matlab命令:
dsolve(‘方程1’, ‘方程2’,…‘方程n’, ‘初始条件’, ‘自变量’)
例如:d²y/dx²=0,对应表达式为D2y=0。
exm:求通解
dsolve('Du=1+u^2','t')
exm:方程组情况
[x,y,z]=dsolve('Dx=2*x-3*y+3*z','Dy=4*x-5*y+3*z','Dz=4*x-4*y+2*z', 't')
xyz分别保存三个未知数的通解
exm:求特解
y=dsolve('D2y+4*Dy+29*y=0','y(0)=0,Dy(0)=15','x')
2.求微分方程的数值解
- 将高阶方程转化为一阶方程组。
- 建立相应的函数文件。
- 调用求解函数solver(ode23、ode45等)。
注:
- 在解n个未知函数的方程组时,x0和x均为n维向量,m-文件中的待解方程组应以x的分量形式写成。
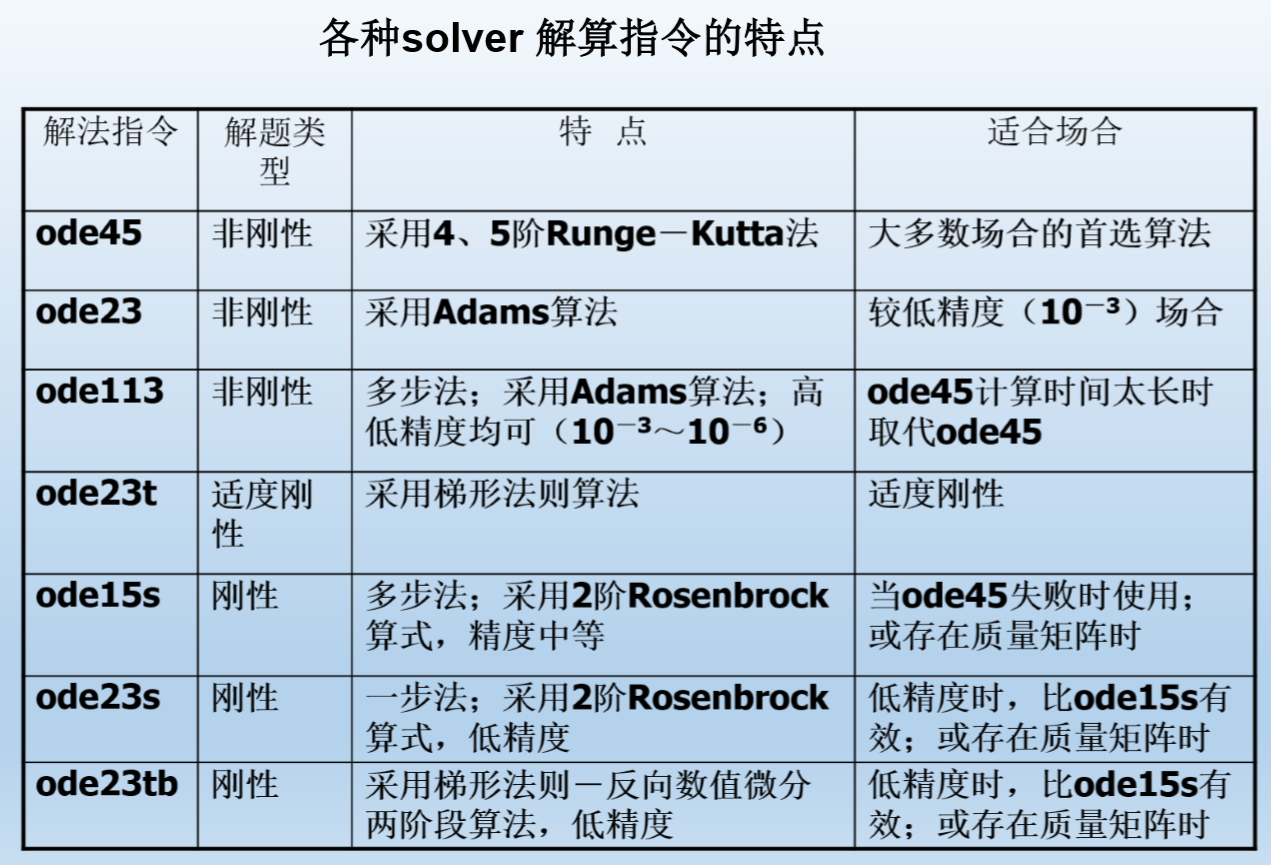
- MATLAB提供了7个常微分方程求解器(solver)分别是ode45,ode23,ode113,ode15s,ode23s,ode23t,ode23tb,其中前3个适用于求解非刚性(Nonstiff)问题,后4个适用于刚性问题。
- 刚性:设有一阶常系数线性微分方程组y’=Ay+f,如果它的Jacobian矩阵的特征值相差十分悬殊;简单点说,就是系统包含多个相互作用但变化速度相差十分悬殊的子过程。

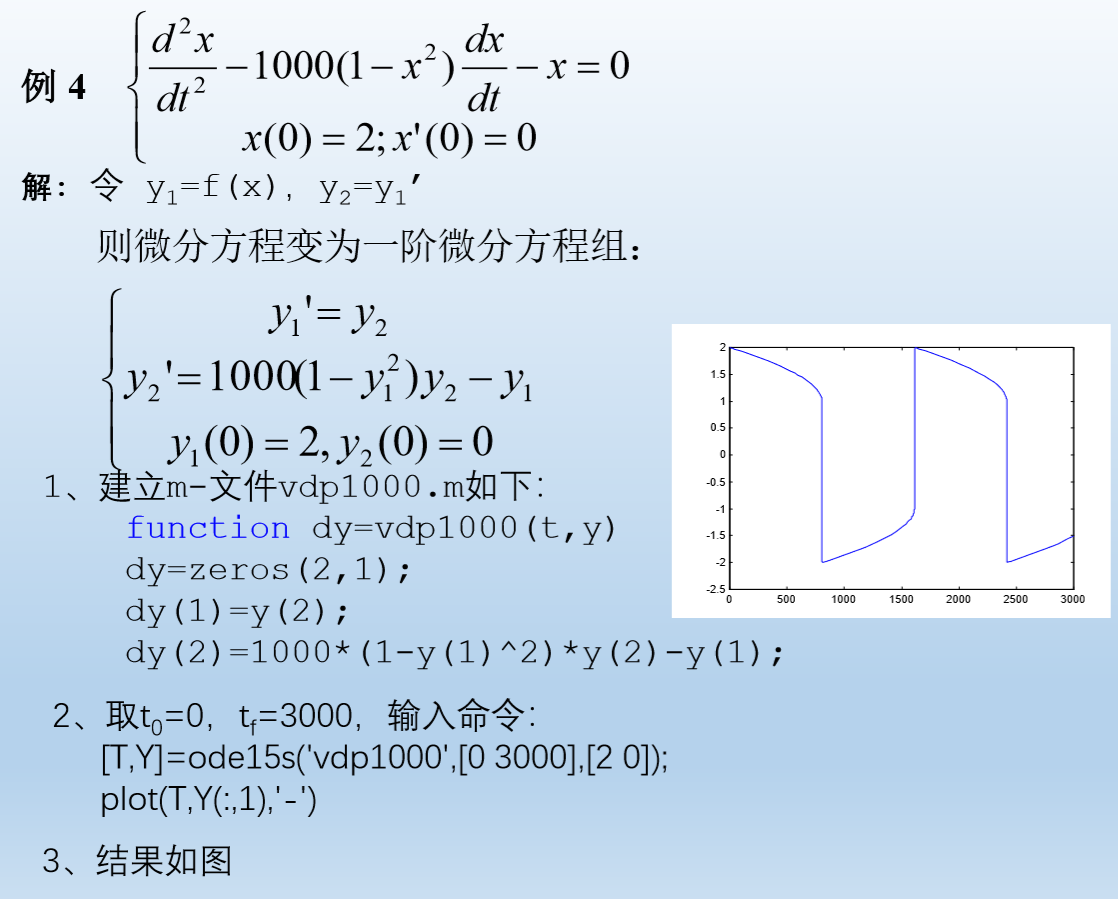
例题
这篇关于【matlab】微分方程建模基础讲解的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



