微分方程_by小崔说数

2024-09-03 04:52

文章标签 微分方程崔说数

本文主要是介绍微分方程_by小崔说数，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

可降解的微分方程

不显含x：y两撇=dp/dx=dp/dy*dy/dx

不显含y：dp/dx

都是y撇等于p

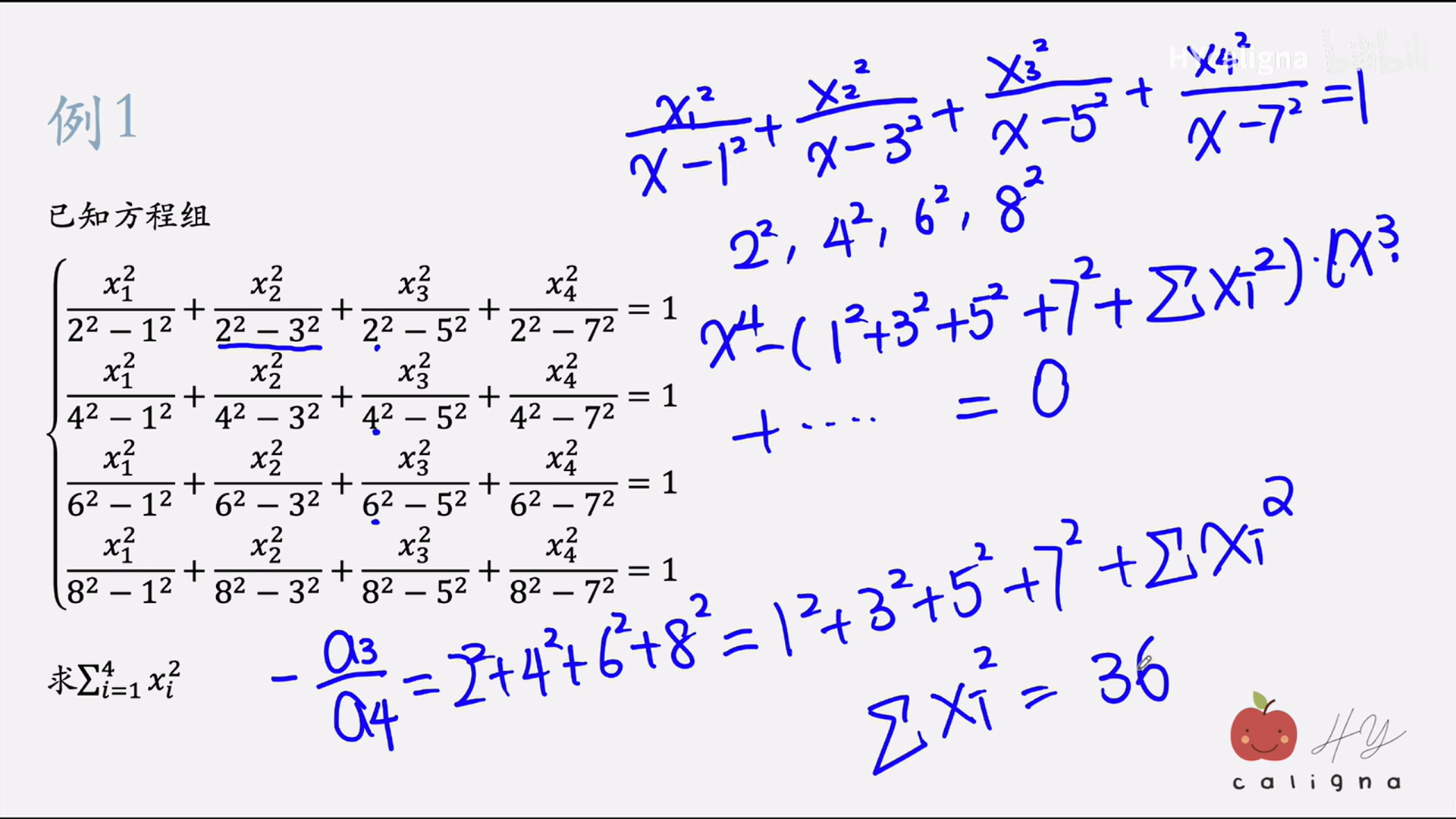
自变量与因变量呼唤

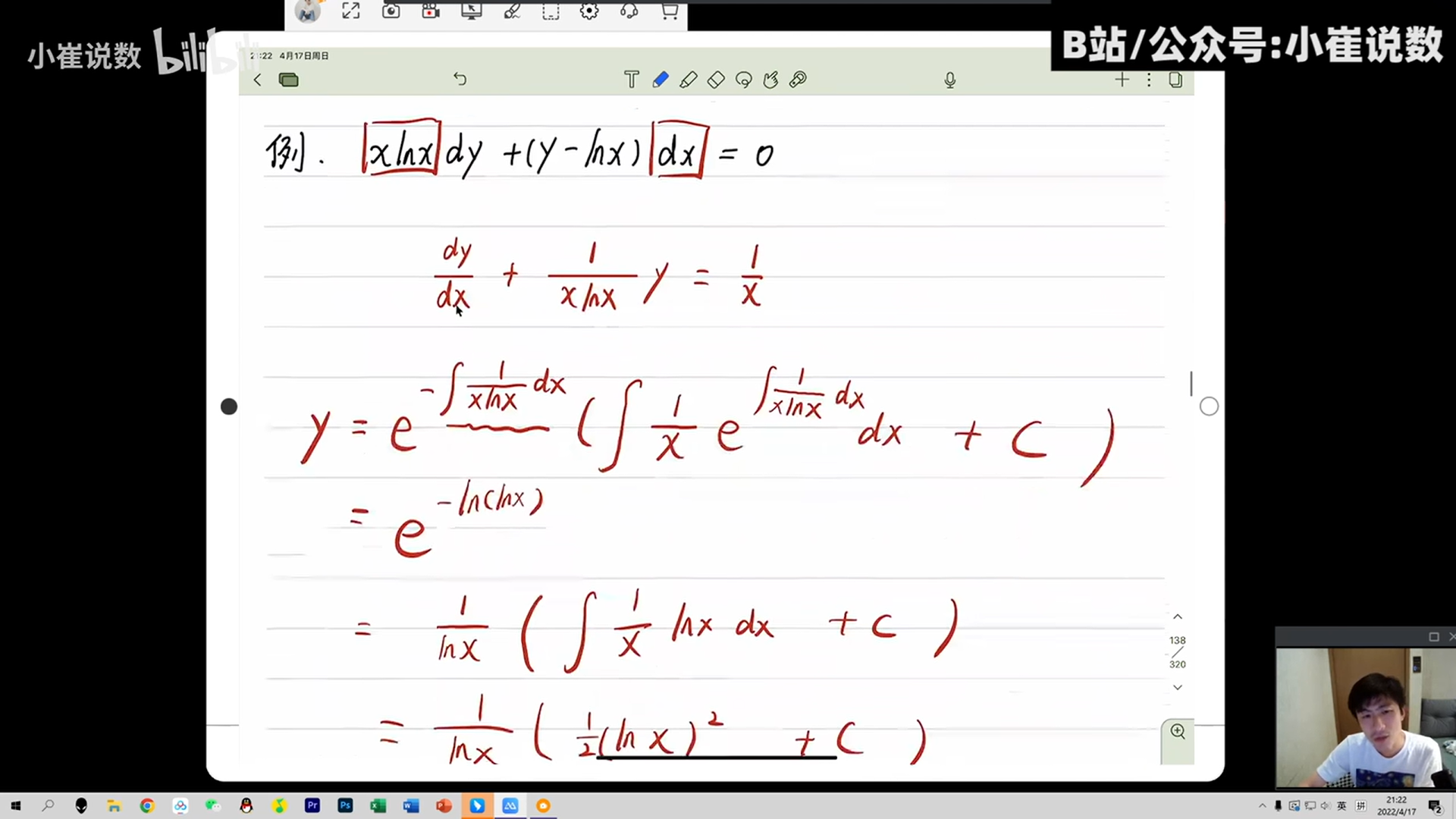
讲解为一阶线性微风方程

，变成可分离得

公式得

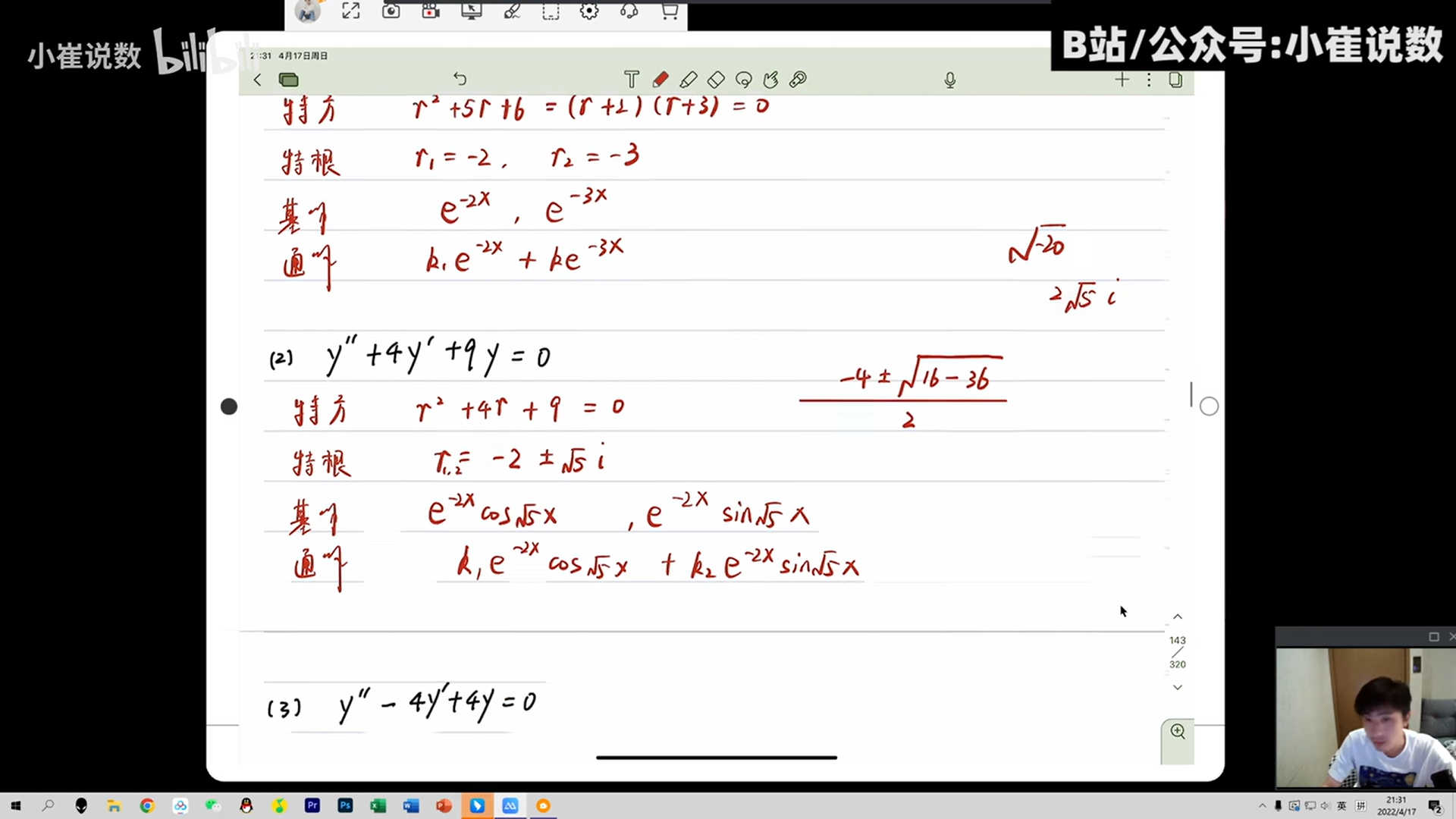
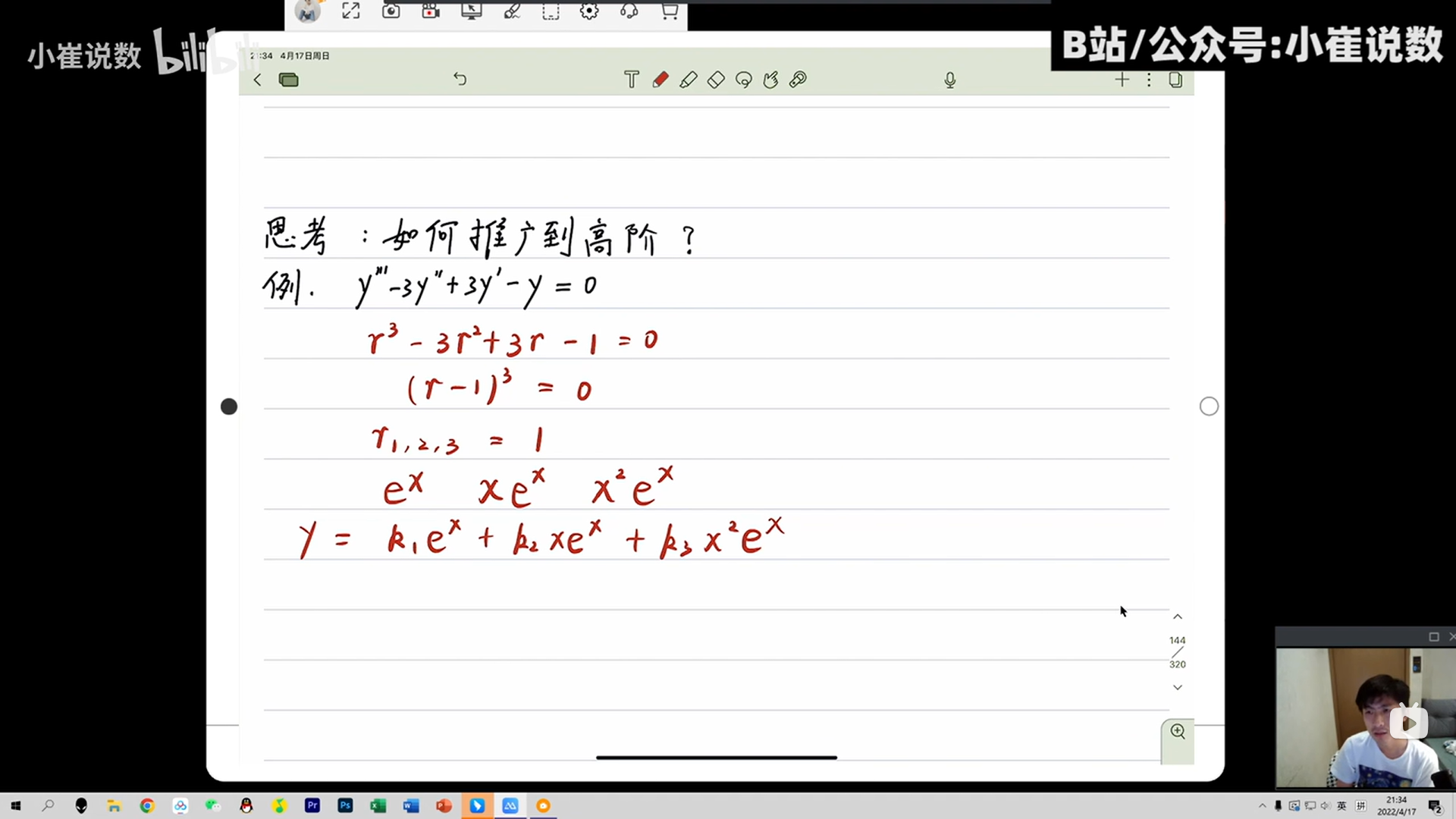
高阶可降解得微分方程

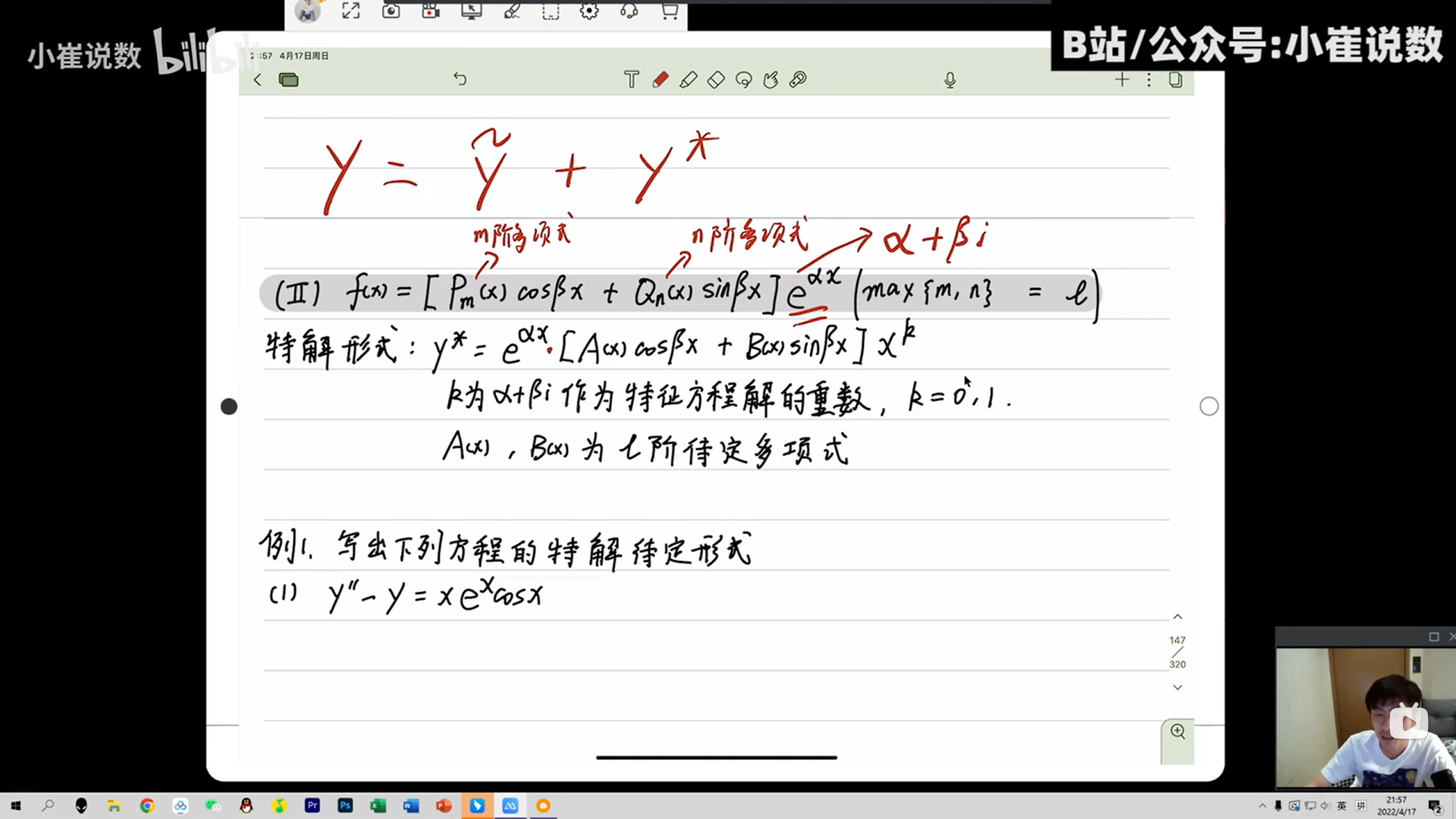
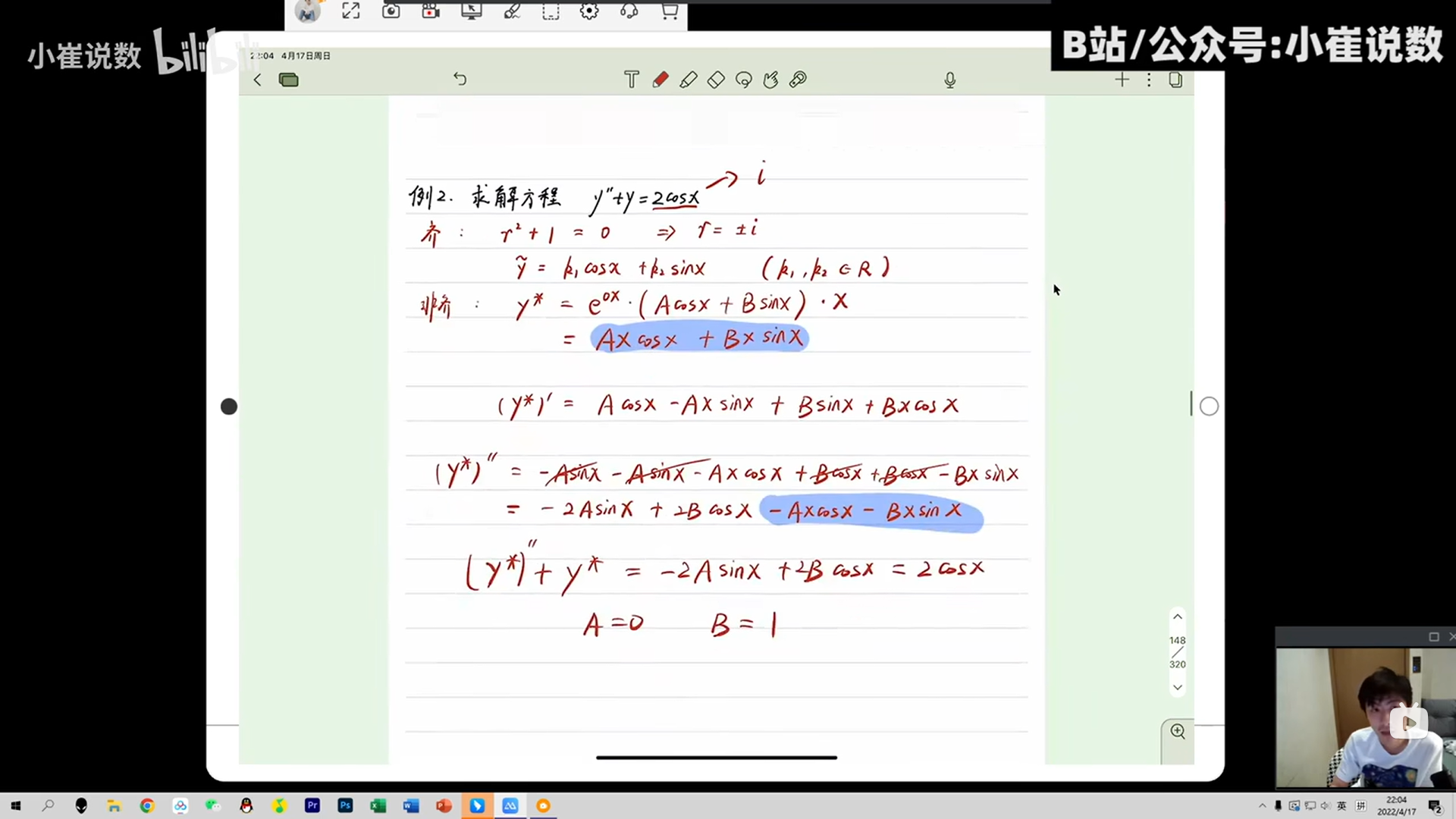
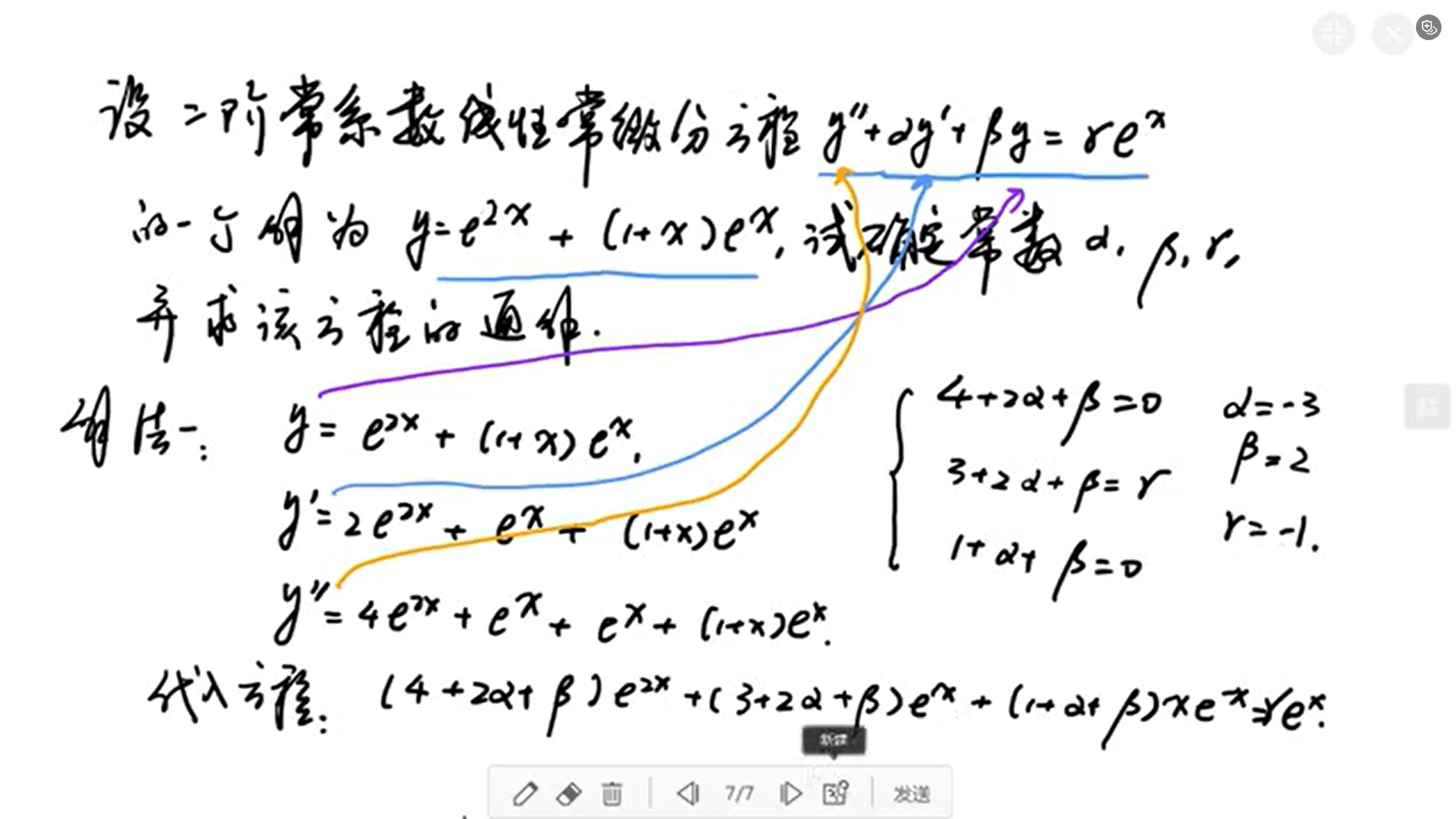
通解=非齐次特解+齐次通解

非齐次特解；解得叠加原理

就是特解得通世

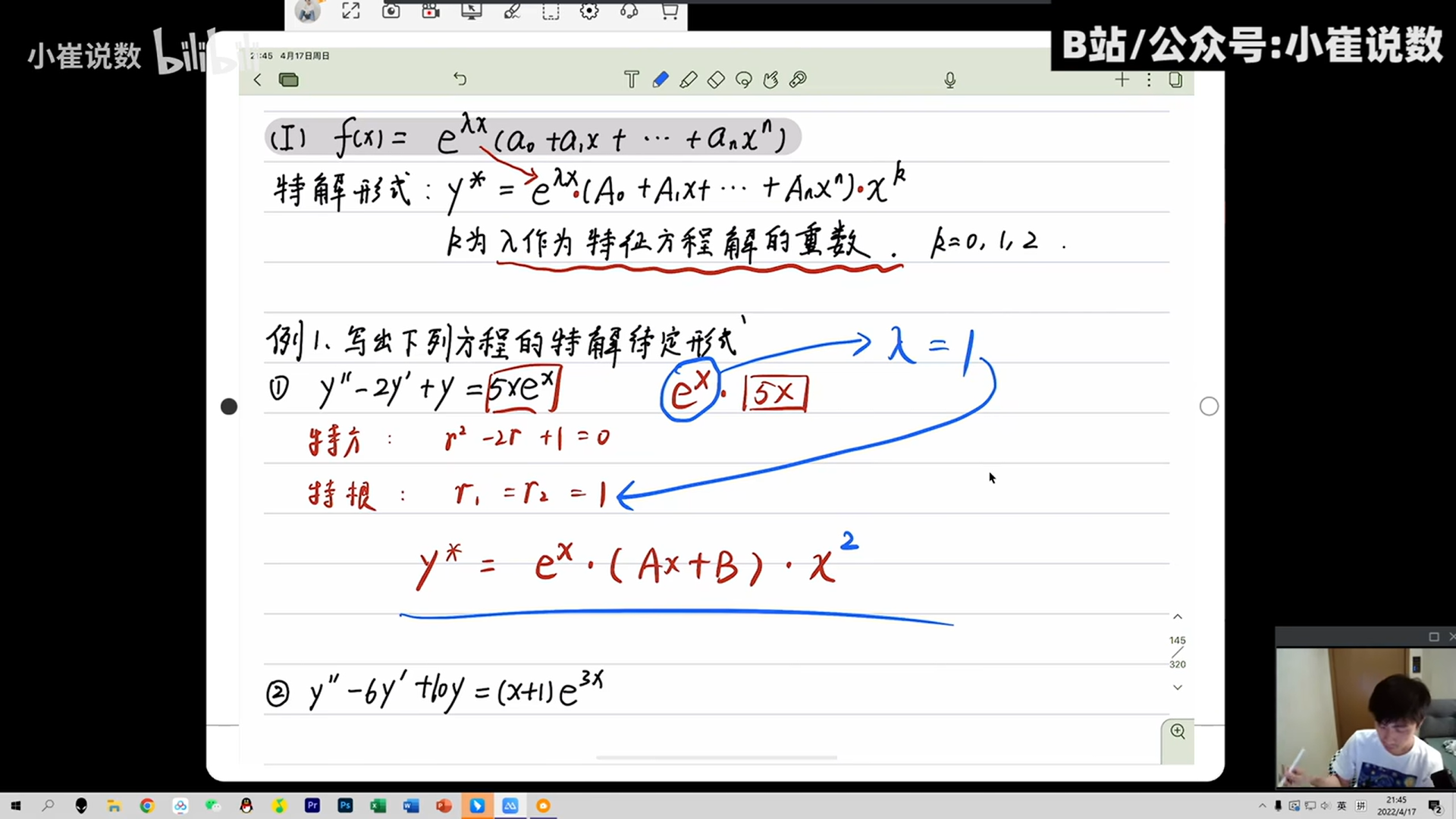
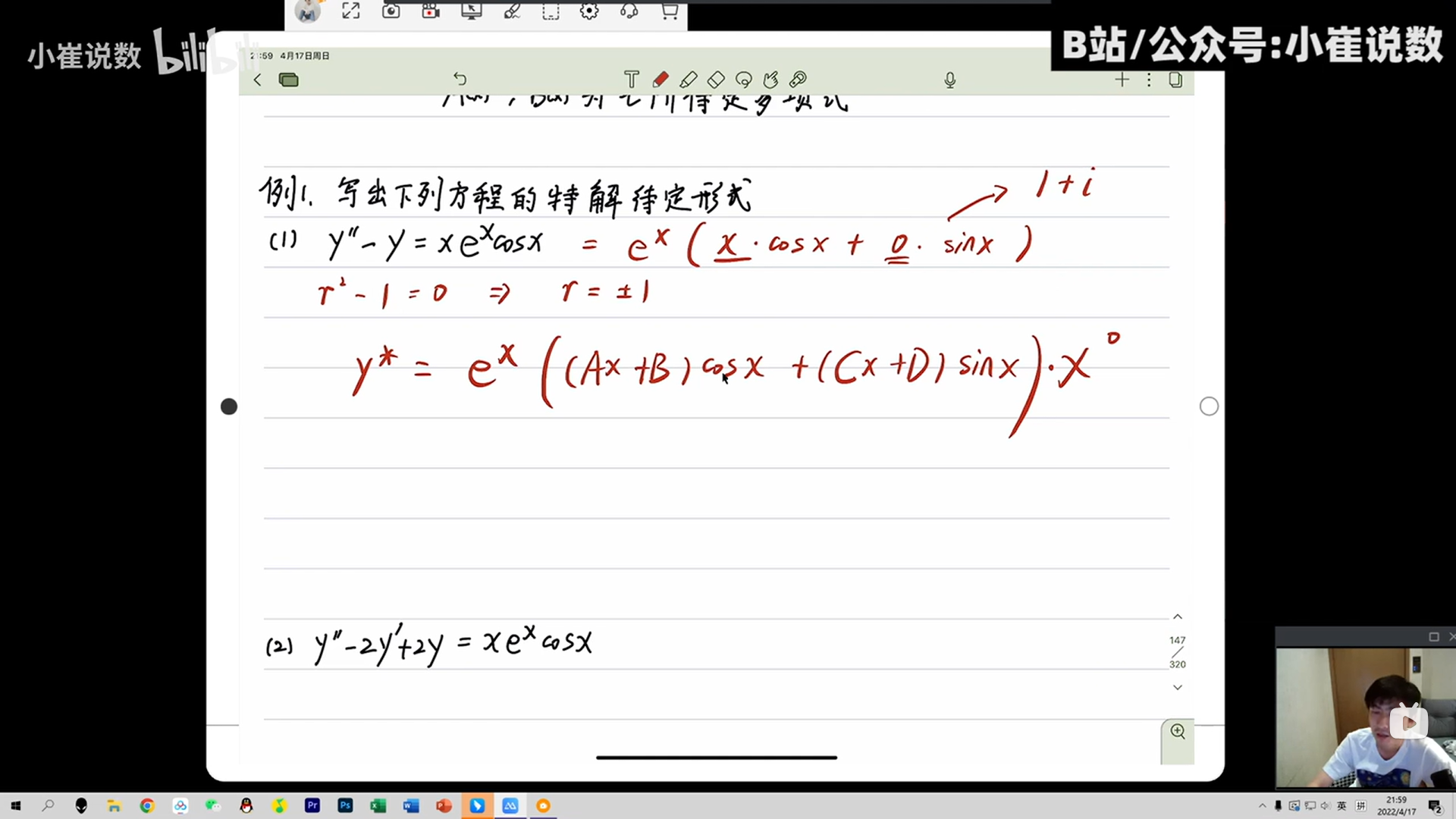
1、待定试

2、e的ax照抄

3、x的k次方

a是特征值的个数

a+bi是否等于特征值

边上先积分求导

常数换元、拆分

1

求导后还有变上限积分、再次求导

化成二阶可降解得微分方程

一直直线相切得条件————1.函数值2、斜率

2

这篇关于微分方程_by小崔说数的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

http://www.chinasem.cn/article/1132082。 23002807@qq.com

深度学习中的可微编程：从微分方程到物理模拟

引言可微编程（Differentiable Programming）是深度学习领域的一个新兴概念，旨在将传统编程中的数学模型（如微分方程）与深度学习模型结合，构建出更加灵活、可解释的模型。这一技术为物理模拟、科学计算等领域带来了新的可能性，使得深度学习不仅能够进行预测，还能融入复杂的物理规律进行精确模拟。本篇博文将探讨可微编程的基本原理、常见应用场景，特别是在物理模拟中的实践，以及未来的发展方

一阶微分方程的解的存在唯一性定理

本篇笔记的内容来源常微分方程(第四版) (王高雄,周之铭,朱思铭,王寿松) 高等教育出版社利普希茨(Lipschitz)条件考虑导数已解出的一阶微分方程 d y d x = f ( x , y ) (1) \frac{\mathrm{d}y}{\mathrm{d}x}=f(x,y)\tag{1} dxdy=f(x,y)(1) 其中 f ( x , y ) f(x,y) f(

东南大学研究生-数值分析上机题（2023）Python 6 常微分方程数值解法

常微分方程初值问题数值解 6.1 题目编制RK4方法的通用程序；编制AB4方法的通用程序（由RK4提供初值）；编制AB4-AM4预测校正方法通用程序（由RK4提供初值）；编制带改进的AB4-AM4预测校正方法通用程序（由RK4提供初值）；对于初值问题 { y ′ = − x 2 y 2 , 0 ≤ x ≤ 1.5 , y ( 0 ) = 3 \begin{cases} y'=-x^{2}y

地震微分方程代码 - 第一部分

Seismic stencil codes - part 1 — ROCm Blogs (amd.com) 2024年8月12日，作者：[Justin Chang](Justin Chang — ROCm Blogs) 和 [Ossian O’Reilly](Ossian O’Reilly — ROCm Blogs)。在高性能计算（HPC）领域，地震工作负载一直以来都依赖于结构网格上的高

微分方程（Blanchard Differential Equations 4th）中文版Section6.3

二阶线性方程 Laplace 变换求解在这一节中，我们将拉普拉斯变换方法扩展到二阶常系数强迫线性方程，即具有以下形式的方程： d 2 y d t 2 + p d y d t + q y = f ( t ) ， \frac{d^2 y}{dt^2} + p \frac{dy}{dt} + qy = f(t)， dt2d2y+pdtdy+qy=f(t)，其中 p p p 和 q q

微分方程（Blanchard Differential Equations 4th）中文版Section5.1

平衡点分析从第3章的工作中，我们能够对线性系统的解有定性和解析的理解。不幸的是，非线性系统通常不容易使用我们开发的解析和代数技术来分析，但我们可以利用线性系统的数学来理解非线性系统在其平衡点附近的行为。 Van der Pol 方程为了说明如何分析平衡点附近解的行为，我们从一个简单但重要的非线性系统——Van der Pol 系统开始。回顾一下，Van der Pol 系统是： d x

齐次二阶微分方程

二阶齐次微分方程的求解过程涉及特征方程的求解。以下是详细的求解步骤：方程形式二阶齐次线性微分方程的标准形式为： a y ¨ ( t ) + b y ˙ ( t ) + c y ( t ) = 0 a\ddot{y}(t) + b\dot{y}(t) + c y(t) = 0 ay¨(t)+by˙(t)+cy(t)=0 其中： - y ( t ) y(t) y(t) 是未知函数； -

微分方程（Blanchard Differential Equations 4th）中文版Section4.4

稳态的振幅和相位系统在本节中，我们回到方程 d 2 y d t 2 + p d y d t + q y = cos ⁡ ω t \frac{d^2 y}{dt^2} + p \frac{dy}{dt} + qy = \cos \omega t dt2d2y+pdtdy+qy=cosωt 用于周期性强迫的阻尼谐振子。我们的目标是建立解决方案行为与参数之间的定量关系——特别是决定强迫频率

微分方程（Blanchard Differential Equations 4th）中文版Section3.5

特殊情况: 重根和零特征值的线性系统在前面的三节中，我们讨论了线性系统 d Y d t = A Y \frac{dY}{dt} = AY dtdY=AY 其中 2 × 2 2 \times 2 2×2 矩阵 A A A 具有两个不同的非零实特征值或一对复共轭特征值。在这些情况下，我们能够使用特征值和特征向量来草绘 x y xy xy 相平面的解，绘制 x ( t ) x(t)

【自动驾驶】控制算法（四）坐标变换与横向误差微分方程

写在前面： 🌟 欢迎光临清流君的博客小天地，这里是我分享技术与心得的温馨角落。📝 个人主页：清流君_CSDN博客，期待与您一同探索移动机器人领域的无限可能。 🔍 本文系清流君原创之作，荣幸在CSDN首发🐒 若您觉得内容有价值，还请评论告知一声，以便更多人受益。转载请注明出处，尊重原创，从我做起。 👍 点赞、评论、收藏，三连走一波，让我们一起养成好习惯😜 在这里，您将

微分方程_by小崔说数

可降解的微分方程

自变量与因变量呼唤

高阶可降解得微分方程

边上先积分求导

1

2

相关文章